4287
Ultimate Intrinsic SNR Based on Expansion Coefficient Optimization for Realistic 3D Macaque Head Model1Interdisciplinary Institute of Neuroscience and Technology, Zhejiang University, Hangzhou, People's Republic of China, 2College of Biomedical Engineering and Instrument Science, Zhejiang University, Hangzhou, People's Republic of China
Synopsis
We have calculated the ultimate SNR at a particular voxel located at monkey cortex through finding the optimized expansion coefficient. Our proposed method enables us to find the relative contribution of divergence free and curl free in UISNR at particular position in the realistic model.
Introduction
To reach the ultimate intrinsic SNR
(UISNR), the corresponding ideal current distribution of spherical and cylinder
phantom with uniform dielectric property can be accurately calculated using
analytical solutions [1]. Recently, a method for calculating the UISNR in
realistic human body model has been proposed, using vector spherical harmonics
and vector cylindrical harmonics as basis set; however, the expansion
coefficient of divergence-free and curl-free component and the ultimate current
distribution of particular voxel position in the realistic model has not been
mathematically specified [2,3]. In this study, we have propose a new method to
calculate UISNR in realistic macaque brain model based on optimization of
expansion coefficient; based on optimized parameters, we further explore the contributions
of div-free and curl-free to the UISNR at cortical regions and have revealed
the ideal current distribution to reach the UISNR.Method
We constructed a spherical current surface covering the entire 3Dmonkey head model (consisting scalp, skull, WM, GM, and CSF, as shown in Fig.1a, with isotropic resolution of 1mm). The radius was set to 5.3cm and the current surface center was placed at the midbrain. We used the following analytical spherical surface current mode as the basis component to mimic all possible conductor distributions on the entire sphere:
$$$K(\theta,\phi)=\sum_(l=1)^L\sum_(m=-l)^lW_(l,m)^(M)X_{l,m}(\theta,\phi)+W_(l,m)^(E)\hat{r}\times X_{l,m}(\theta,\phi)$$$
Where X is vector spherical harmonic of order (l, m). and WM and WE are the series expansion coefficients representing divergence-free (loop like) and curl-free (dipole like) surface current contributions, respectively. Because the ultimate basis set relating to expansion coefficients are unknown, we applied genetic algorithm (global optimization method) to generate and find the optimized series expansion coefficients. The B field and E field inside the monkey head model generated by the surface current pattern were calculated through the fast open-source volume-integral solver MARIE [4] in MATLAB. Then, we calculated the SNR at target voxel according to equation in [5].
Results
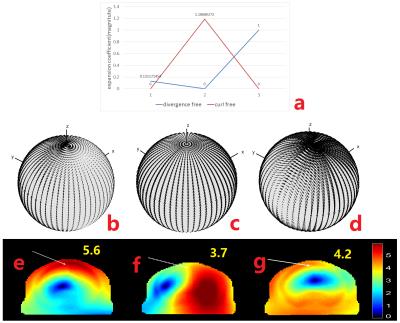
Figure 1b shows the position of the monkey
head model relative to the spherical surface current pattern. Figure2a shows
the 1st order expansion coefficient; Figure 2b-d show the ideal surface current
distribution consisting of both div-free and curl-free component, curl-free
component alone, and div-free component alone, respectively; Figure2e-f show the
UISNR on the same coronal slice that is generated from the calculated ideal
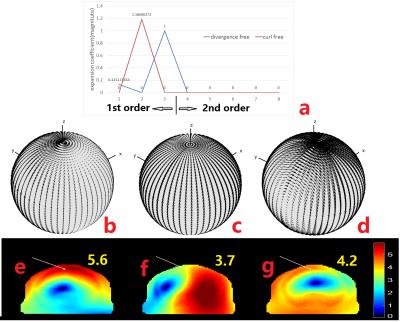
surface current. Figure 3 shows, for the 2nd order expansion coefficient, the
results of same measures as depicted in Figure 2.
From the overall amplitude of the expansion
coefficient in figure 2a, we find that the contributions of divergence free and
curl free components to the UISNR current is very close. The area of high SNR related
to div-free current is located at deep brain area, while the area of high SNR
related to curl-free component is mainly accumulated at periphery. The SNR of
chosen voxel related to both div-free and curl-free components is also very
close, which is consistent with conclusion indicated by expansion coefficient.
In the meantime, the second order part of optimized
expansion coefficient are all zero, implying that the UISNR may have converged at
the first order. Therefore, the surface current pattern and related spatial SNR
distribution are almost the same with first order.Discussion
The chosen voxel position is relatively far
from the spherical surface current, which may explain why the UISNR may have converged
at the first order. Nevertheless, the distribution of optimized first-order expansion
coefficient is very similar to the calculated coefficient using analytical
method on uniform spherical phantom. The SNR distribution in the monkey brain of
each component is also consistent with the prior knowledge of distribution of
loop coil (div-free) and dipole (curl-free).Conclusion
We have calculated the ultimate SNR at a
particular voxel located at monkey cortex through finding the optimized
expansion coefficient. Our proposed method enables us to find the relative
contribution of divergence free and curl free in UISNR at particular position
in the realistic model. The optimized coefficient with higher orders and
current pattern at other tissue positions in the macaque brain will be explored
in future work.Acknowledgements
We would like to thank Dr. Riccardo Lattanzi for technical support. This work was supported in part by Fundamental Research Funds for the Central Universities (2016QN81018).References
1. Lattanzi R. MRM 68, 2012, p. 286-304.
2. Andreas P. Proc. ISMRM 24, 2016, p. 0175
3. Guerin B. Proc. ISMRM 22, 2014, p. 617.
4. https://github.com/thanospol/MARIE
5. Lattanzi R. NMR in Biomed 23: p. 142-151, 2009.
Figures