Synopsis

A novel method for long-T₂ suppression in 3D-UTE imaging is introduced. The method is based on long- and short-T₂ components phase states in a dual-segment acquisition scheme (digital summation of two k-spaces before reconstruction, respectively acquired with and without adiabatic inversion), and offers a substantial contrast-to-noise ratio over the different components. We compare our method to the state-of-the-art IR-UTE. It shows higher performance and efficiency in terms of signal suppression and short-T₂ contrast.

Purpose

Theory

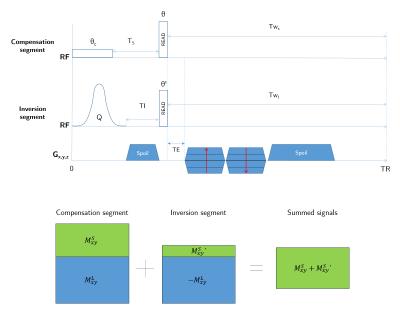
The method employed (fig. 1) consists in a 2-part sequence: one segment (referred hereafter to as “compensation”) composed of a long ($$$\gg$$$$$$T_2^{short}$$$) rectangular-pulse followed by a short one, and one segment (hereafter called “inversion”) similar to the IR-UTE method. Inversion time TI and $$$\theta'$$$ are optimized along with $$$\theta_{c}$$$ and $$$\theta$$$ so that the sum of acquired k-spaces from both segments yields a long-T₂-free one while short-T₂ component is maximized through the optimization process introduced below. Here, we take advantage of the long-T₂ signals being in opposite phases in the different segments to yield a proper suppression. Meanwhile the short-T₂ ones stay in phase since at most saturated by the adiabatic inversion pulse (Q=0)⁵. Hence, the sum of signals is therefore theoretically exclusively composed of short-T₂ signal. The use of the compensation pulse gives an additional degree of freedom, all the more important as its long duration is taken into account in the optimization process for short-T2 signal maximization.

Signal quantities can be generally expressed after respective readout pulses ($$$\theta/\theta'$$$) using the Bloch equations:

$$M_{xy}=M_0\frac{(1-E_s)+E_s(1-E_w)f_{z_{C}}}{1-f_{z_{C}}f_zE_SE_w}f_{xy}$$

$$M_{xy}'=M_0\frac{(1-E_I)+E_I(1-E'_w)Q}{1-Qf'_zE_IE'_w}f_{xy}',$$

with $$$E_s=e^{-T_s/T1}$$$, $$$E_I=e^{-TI/T1}$$$, $$$E_w=e^{-T_{w_s}/T1},E_w'=e^{-T{w_I}/T1}$$$,

$$$f_{z}=e^{-\tau/2T_2}\Big[\cos\big(\sqrt{\alpha^2-(\tau/2T_2)^2}\big)+\tau/2T_2\text{sinc}\big(\sqrt{\alpha^2-(\tau/2T_2)^2}\big)\Big]$$$,

$$$f_{xy}=e^{-\tau/2T_2} \alpha\text{sinc}\big(\sqrt{\alpha^2-(\tau/2T_2)^2}\big)$$$ ($$$\tau$$$ being respective pulse durations and $$$\alpha$$$ corresponding flip angles) as described in [6], and $$$Q$$$ inversion efficiency $$$(Q \in [-1,1])$$$.

Thus, suppressing the long-T₂ component and maximizing the short-T₂ one can be reduced to a 4-parameters optimization problem over $$$\theta, \theta’, \theta_C$$$ and TI:

$$\text{argmin}\|\sum_{i=1}^2\omega_i\phi_i\|_2^2,$$

with $$$\omega_i$$$ weightings,

$$$\phi_1=|M_{xy}^{L}(\theta,\theta_{C})-|M_{xy}^{'L}(\theta',TI)||$$$,

and $$$\phi_2=(M_{xy}^{S}(\theta,\theta_{C})-M_0)+(M_{xy}^{'S}(\theta',TI)-M_0)$$$ ($$$L$$$ and $$$S$$$ superscripts stand for long and short, respectively).

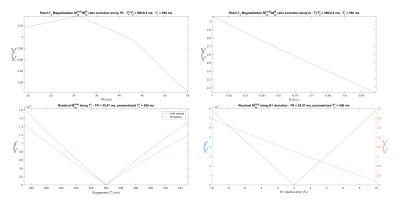
Simulations of signal enhancement compared to the IR-UTE method and signal suppression theoretical efficiency were performed (fig. 2). Both segments are somehow similar to the Actual Flip Angle sequence⁷, except that the consecutive pulses are different (stretched hard or adiabatic pulses). Thus, gradient spoiling, RF spoiling and delays (such as $$$T_s$$$ and $$$T_{w_{I/s}}$$$) are set to ensure a proper spoiling of the long-T₂ component, and a minimal impact of potential static gradients⁸. Spoiling parameters (gradient/RF phase) were optimized in simulations using the EPG formalism⁹.

Method

Experiments were conducted on a 7T BioSpec 70/30 USR small animal MRI system (Bruker BioSpin MRI GmbH, Ettlingen, Germany). The phantom was composed of a Lego brick (T₁/T₂$$$\approx$$$500/0.5 ms at 7T) immersed in a 1 mM Ni²⁺,2Cl^- solution (D=1.81.10^-9 m²/s, T₁/T₂=550/290 ms). Scans were performed using a 86 mm diameter transmitter and a mouse surface coil for reception.

Common sequence parameters were: repetition time=25.07 ms, TE=25 $$$\mu$$$s, RF-phase increment $$$\phi_0$$$=10°, receiver bandwidth=150 kHz, matrix size=96x96x96, voxel dimension=0.26 mm isotropic, number of radial lines=28733, dummy scans=184. Specific parameters were:

InoR-UTE: $$$T_s/TI/T_{w_{s}}/T_{w_{I}}$$$=4/3/20/15 ms, $$$\tau_{inv}$$$=7 ms (hyperbolic secant), $$$\tau_{comp}$$$=1 ms, $$$\tau_{read}$$$=70 $$$\mu$$$s, $$$\theta_{C}$$$=78°, $$$\theta$$$=36.3°, $$$\theta'$$$=90°, $$$G_{spoil}^{comp}\times t_{spoil}^{comp}$$$=1060.2/5301.0 mT/m.s, $$$G_{spoil}^{inv}\times t_{spoil}^{inv}$$$=706.8/3534.0 mT/m.s, scan time=24min20s;

IR-UTE: $$$TI/T_{w_{I}}$$$= 9/9 ms (TI was chosen to theoretically suppress the long-T2 component given the sequence parameters), $$$\tau_{inv}$$$=7 ms (hyperbolic secant), $$$\tau_{read}$$$=70 $$$\mu$$$s, $$$\theta_{IR}$$$=90°, $$$G_{spoil}^{IR}\times t_{spoil}^{IR}$$$=706.8/3534.0 mT/m.s, 24 averaging to reach a sufficient SNR, scan time=4h48min.

Results

Conclusion

Acknowledgements

References

1. Du, J. et al., Dual inversion recovery, ultrashort echo time (DIR UTE) imaging: Creating high contrast for short-T2 species, MRM 2010; 63:447-455

2. Du, J. et al., Short T2 contrast with three-dimensional ultrashort echo time imaging, MRM 2011; 29:470-482

3. Larson, P. et al., Designing long-T2 suppression pulses for ultrashort echo time imaging, MRM 2006; 56:94-103

4. Deligianni, X. et al., Water-selective excitation of short-T2 species with binomial pulses, MRM 2014; 72:800-805

5. Li, C. et al., Comparison of optimized soft-tissue suppression schemes for ultrashort echo time MRI, MRM 2012; 68:680-689

6. Sussman, M., Design of practical T2-selective RF excitation (TELEX) pulses, MRM 1998; 40:890-899

7. Yarnykh, V. et al., Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field, MRM 2007; 57:192-200

8. Nehrke, K., On the steady-state properties of actual flip angle imaging (AFI), MRM 2009; 61:84-92

9. Weigel, M., Extended phase graphs: Dephasing, RF pulses, and echoes - pure and simple, JMRI 2015; 41:266-295