4031
Long-T2 suppression based on saturation and diffusion in a steady-state 3D-UTE sequence1Université de Strasbourg, CNRS, ICube, FMTS, Strasbourg, France, 2Institut Mines Télécom, Télécom Bretagne, INSERM LaTIM, Brest, France
Synopsis
A new method for long-T2 suppression in a prepared steady-state 3D-UTE sequence is introduced. The method is based on long-T2 signal behavior in steady-state as the diffusion-inducing spoiling gradients are modified, giving a theoretical signal cancellation using appropriate coherence combinations. At the same time, short-T2 signal quantity is optimized, offering a positive contrast over this component. Imaging experiments over a Lego brick soaked in doped water show an excellent agreement with theoretical predictions.
Purpose
Imaging of the very-short T2 tissues is challenging in that the signal decays very rapidly (T2 < 1ms), as well as its signal quantity being often overwhelmed by long-T2 components (fat, free-water). Nevertheless, direct imaging of such components may significantly improve specificity in tissues evaluation. Numerous methods to highlight these species exist using a proper preparation (Inversion-Recovery modules1, saturation module2 or more complex and specific long-T2 suppression pulses3) or a specific excitation pattern4 to either null the undesired signal or to selectively excite the component of interest. In this work, we explore a novel method for long-T2 suppression in a steady-state 3D-UTE sequence taking advantage of diffusion and coherence effects while acquiring short-T2 components. Simulations and analysis were performed using the Extended Phase Graph (EPG) formalism5,6.Theory
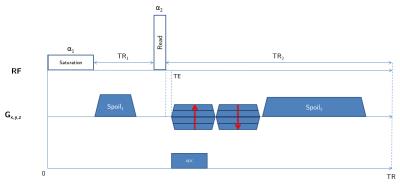
The pulse sequence employed (fig. 1) consists in a long ($$$\gg T_2^{short}$$$) rectangular saturation pulse followed by a short one ($$$\alpha_2 \leq$$$ 90°), whose flip angle will be computed to maximize the short-T2 signal. It’s very similar to the Actual Flip Angle sequence7, except that $$$\alpha_1\neq\alpha_2$$$. Gradient spoiling, RF spoiling and delays are optimized to ensure a steady-state of the long-T2 component to be suppressed, and a minimal impact of potential static gradients (e.g. B0 inhomogeneities)8.
First, the short-T2 transverse magnetization can be tracked using the Bloch equations in steady-state:
$$M_{xy}=M_0\frac{(1-E_s)+E_s(1-E_w)f_{z_{1}}}{1-f_{z_{1}}f_{z_{2}}E_sE_w}f_{xy},$$
with $$$E_s=e^{-TR_1/T1},E_w=e^{-TR_2/T1}$$$,
$$$f_{xy}=e^{-\tau_2/2T_2} \alpha_2\text{sinc}\big(\sqrt{\alpha_2^2-(\tau_2/2T_2)^2}\big)$$$,
$$$f_{z_i}=e^{-\tau_i/2T_2}\Big[\cos\big(\sqrt{\alpha_i^2-(\tau_i/2T_2)^2} \big)+\tau_i/2T_2\text{sinc}\big(\sqrt{\alpha_i^2-(\tau_i/2T_2)^2}\big)\Big]$$$ ($$$\tau_i$$$ pulse duration) as described in [9]. These quantities account for the signal loss during a RF pulse caused by T2 relaxation.
The short-T2 signal can therefore be maximized with respect to $$$\alpha_2$$$ (given a first flip angle $$$\alpha_1$$$ = 90°) with $$$\hat{\alpha_2}=\text{argmin}_{\alpha_2}(M_0-M_{xy}(E_s,E_w,f_{z_1},f_{z_2},f_{xy}))$$$.
Then, with $$$\alpha_2$$$ set, we take advantage of the steady-state to suppress the water signal. Using the expression of configuration states in [5], the signal to be suppressed can be written:
$$F_0^+=\cos(\alpha_2/2)^2F_{0}^-+e^{2i\Phi}\sin(\alpha_2/2)^2F_0^{-*}-ie^{i\Phi}\sin(\alpha_2)Z_{0}^{-},$$
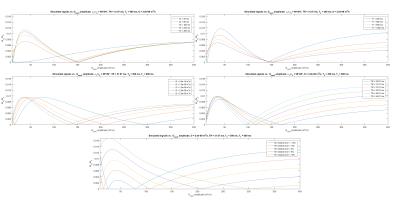
with $$$F_0$$$ and $$$Z_0$$$ being functions of $$$\alpha_1,\alpha_2$$$, RF-phase $$$\Phi,n=TR_2/TR_1,TR_2,TR_1,T_1^{long},T_2^{long}$$$ and diffusion coefficient $$$D$$$. In this case, having $$$|F_0^+|=0$$$ would imply a complete long-T2 suppression. Since no trivial analytical expression exists for the $$$F_0^-$$$ and $$$Z_0^-$$$ states in steady-state, we numerically explored the tissues and sequence parameters space in order to assess whether the diffusion effect induced by the spoiling gradients would combine the $$$F_0^-$$$ and $$$Z_0^-$$$ states in order to satisfy $$$|F_0^+|=0$$$. Using the EPG formalism, we have shown that this condition can be met for sets of parameters and RF-phase increment $$$\Phi_0=k\times360/(n+1)$$$ $$$(k \in \mathbb{N})$$$ (fig. 2), offering a signal falling to 0 (referred hereafter to as “signal pit”).
Method
Experiments were conducted on a 7T BioSpec 70/30 USR small animal MRI system (Bruker BioSpin MRI GmbH, Ettlingen, Germany). The phantom was composed of a Lego brick (T1/T2 $$$\approx$$$ 500/0.5 ms at 7T) immersed in a 1 mM Ni2+,2Cl- solution (D = 1.81.10-9 m²/s, T1/T2 = 550/290 ms). Sequence parameters were: repetition time = 31.07 ms (TR1/TR2 = 5/25 ms (n = 5), $$$\tau_{1}$$$ = 1 ms, $$$\tau_{2}$$$ = 70 $$$\mu$$$s), TE = 50 $$$\mu$$$s, $$$t_{spoil}$$$ = 2/10 ms, $$$\alpha_1/\alpha_2$$$ = 90°/64°, RF phase increment $$$\Phi_0$$$ = 0°, receiver bandwidth = 150 kHz, matrix size = 96x96x96, voxel dimension = 0.26 mm isotropic, number of radial lines = 28733, dummy scans = 184, acquisition time/scan = 14min52s. To confirm the diffusion effect induced by the spoiling gradients, 23 amplitude values linearly spaced from 44 to 336 mT/m were used for the latter. Scans were performed using a 86 mm diameter transmitter and a mouse surface coil for reception.Results
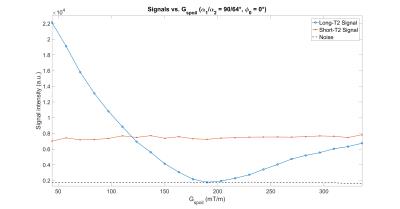
Fig. 3 shows doped water and Lego brick signals evolution along $$$G_{spoil}$$$ amplitude, and demonstrates the existence of a signal decrease for the long-T2 component, obviously capped to the noise level. While the long-T2 signal is being nulled, there’s no impact over the short-T2 component, consequently offering a good contrast. Fig. 4 shows slices highlighting this effect, where a positive contrast over the Lego brick is made visible.Conclusion
We demonstrated the possibility of an efficient long-T2 signal cancellation by using a saturation-based sequence along with an appropriate damping induced by spoiling gradients in a prepared 3D-UTE imaging experiment, allowing for short-T2 components highlighting. The short scan duration seems promising for a whole brain short-T2 tissues exploration.Acknowledgements
No acknowledgement found.References
1. Du, J. et al., Dual inversion recovery, ultrashort echo time (DIR UTE) imaging: Creating high contrast for short-T2 species, MRM 2010; 63:447-455
2. Du, J. et al., Short T2 contrast with three-dimensional ultrashort echo time imaging, MRM 2011; 29:470-482
3. Larson, P. et al., Designing long-T2 suppression pulses for ultrashort echo time imaging, MRM 2006; 56:94-103
4. Deligianni, X. et al., Water-selective excitation of short-T2 species with binomial pulses, MRM 2014; 72:800-805
5. Weigel, M., Extended phase graphs: Dephasing, RF pulses, and echoes - pure and simple, JMRI 2015; 41:266-295
6. Weigel, M. et al., Extended phase graphs with anisotropic diffusion, JMR 2010; 205:276-285
7. Yarnykh, V. et al., Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field, MRM 2007; 57:192-200
8. Nehrke, K., On the steady-state properties of actual flip angle imaging (AFI), MRM 2009; 61:84-92
9. Sussman, M., Design of practical T2-selective RF excitation (TELEX) pulses, MRM 1998; 40:890-899
Figures