4026

Accelerated Adaptive Quasi-Random Single-Point Imaging for in vivo Artefact Reduction
Tobias Speidel1 and Volker Rasche2

1Core Facility Small Animal Imaging, University of Ulm, Ulm, Germany, 2Department of Internal Medicine II, University of Ulm, Ulm, Germany

Synopsis

MR imaging of short relaxation times spin systems has been a widely discussed topic with serious clinical applications and led to the emergence of fast imaging ultra-short echo-time sequences such as UTE and ZTE. Nevertheless, these sequences suffer from image blurring due to the related point-spread function and are highly prone to imaging artefacts arising from e.g. chemical shifts or magnetic susceptibilities. In this work, we present a fully functional concept of spherical quasi-random single-point imaging that is highly acceleratable due to intrinsic undersampling properties and capable of strong metal artefact suppression with high tissue contrast.

Introduction

Radial single-point imaging sequences such as the SPRITE1 sequence have widely been discussed by outlining their capability of imaging tissues with short $$$T_2^\star$$$ relaxation times also concerning in vivo applications2. Despite their promising properties, single-point imaging methods are rarely adopted to a wider field of applications due to corresponding long acquisition times. A solution to this limitation can be the extensive use of undersampling with simultaneous quasi-random sampling and a combination with non-linear optimization reconstruction techniques like Compressed Sensing. Another challenging aspect of unconventional trajectory design includes the calculation of weighting factors for each respective acquired point in $$$k$$$-space. In this work, we address all necessary issues and demonstrate solutions in order to achieve an efficient routine of accelerated random sampling.

Methods

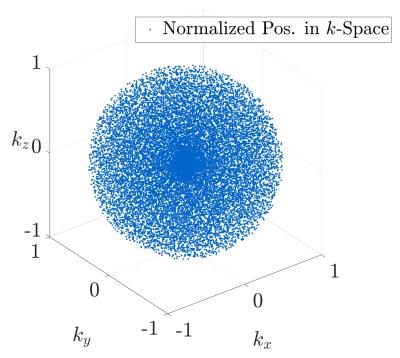
The basic sampling scheme is based on the requirements defined by the mathematical properties of Compressed Sensing. Strictly speaking, a trajectory is favourable which leads to random noise-like undersampling artefacts during undersampled imaging. We have therefore created a three-dimensional spherical quasi-random trajectory, following the Sobol base-2 low-discrepancy algorithm, with an isotropic centre-oversampling using a quadratic density function. Figure 1 shows the final trajectory with exemplary twenty-thousand three-dimensional points. Twenty percent of these points were backfolded around the centre of $$$k$$$-space to realize a generally applicable centre-oversampling.

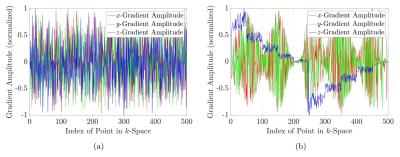
The generated Sobol point sets are not ordered, leading to large gradient ramps between most of the successive coordinates. This is highly inefficient in terms of the gradient duty cycle. Sorting according to travelling salesman algorithms would yield the best possible trajectory, but it suffers from a very high computational complexity $$$\mathcal{O}(N^2 2^N)$$$. Therefore a sorting algorithm was implemented, which divides the sphere into slices along a primary direction and sorts all points within the slice along a secondary direction. Figure 2 shows the comparison of the normalized gradient amplitudes with respect to the index of the point-set of the trajectory for the unsorted and the sorted trajectory.

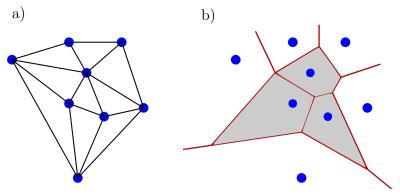
Since the low-discrepancy trajectory does not follow any regular geometrical behaviour, the implementation of a Dirichlet tessellation for reconstruction is necessary3.

We define a finite set of points $$$\{\vec{x_i}\colon\, i=1,...,N\}$$$ and call each element $$$\vec{x_i}$$$ a generator of a Voronoi cell in the Euclidean space $$$\mathbb{R}^n$$$. The Voronoi cell of a generator is then defined as

$$\mathcal{V} := \{\vec{x_i} \in \mathbb{R}^n \, | \, \mathcal{P}_i(\vec{x}) < \mathcal{P}_j(\vec{x}) \, \, \forall j\neq i\},$$

where $$$\mathcal{P}_i$$$ is a given set of continuous, generalized square distance functions on $$$\mathbb{R}^n$$$. Since $$$\forall i\colon\, \vec{x_i} \in \mathcal{V}_i$$$, any point $$$\vec{x} \in \mathcal{V}_i$$$ is closer to $$$\vec{x_i}$$$ than to any other $$$\vec{x_j}$$$ with $$$i \neq j$$$. Additionally, each $$$\mathcal{V}_i$$$ represents an open neighbourhood of $$$\vec{x_i}$$$.

In general, the complete Voronoi tessellation of a set of points $$$\{\vec{x_i}\colon\, i=1,...,N\}$$$ within $$$\mathbb{R}^n$$$ is given by the set of all Voronoi cells with their respective contact boarders $$$\zeta_{ij}$$$ for all $$$\vec{x_i}$$$. The Voronoi tessellation $$$\{\mathcal{V}_i,\zeta_{ij};i,j=1,...,N\}$$$ then covers the complete space with $$$\zeta_{ij} = \overline{\mathcal{V}}_i \cap \overline{\mathcal{V}}_j$$$ for $$$i \neq j $$$ and is therefore unbounded. In this work, the Euclidean square distance function $$$\mathcal{P}_i(\vec{x}) = (\vec{x}-\vec{x_i})^2$$$ was used. Such a Voronoi tessellation is depicted in figure 3 aside with the corresponding Delaunay triangulation from which the Voronoi tessellation is obtained by dividing the connections in a perpendicular way.

Results and Discussion

The low-discrepancy trajectory shows ideal noise-like undersampling properties for the combination with Compressed Sensing, leading to high tissue contrast at excellent SNR. The acquisition time of the presented volume scan can be reduced to $$$\approx 5.5$$$ min. Figure 4 and figure 5 show two orthogonal slices of a mouse femur, penetrated with a titanium pin with surrounding tissue, acquired using the Bruker BioSpec 117/16 USR system. Both figures compare the original SPI image with a corresponding ZTE and show the result of the reconstruction using Compressed Sensing at eight-fold undersampling.

The unsorted trajectory shows a mean absolute value of change in normalized gradient amplitude of 0.3545 mT/m between successive points while the sorted trajectory shows a mean of 0.0496 mT/m. The mean of the trajectory created using a travelling salesman implementation is 0.0732 mT/m. The sorted trajectory following figure 2b is capable of reducing the duty cycle by a maximum of 13 % in comparison to the unsorted trajectory.

Conclusion

We presented a highly efficient imaging and reconstruction technique based on a low-discrepancy sequence in combination with Dirichlet tessellations and non-linear optimization that permits random single-point imaging at short acquisition times. The presented images are nearly free of any susceptibility related artefact with significant signal arising from tissues with short $$$T_2^\star$$$ relaxation times.

Acknowledgements

No acknowledgement found.

References

1. I. V. Mastikhin, B. J. Balcom, P. J. Prado, C. B. Kennedy. SPRITE MRI with Prepared Magneti- zation and Centric k-Space Sampling. Journal of Magnetic Resonance. 136, 159-168, 1999.

2. J. Kuriyan, B. Konforti and D. Wemmer. A comparison of UTE versus SPRITE for Robust MR Imaging of short T2 components. Proc. Intl. Soc. Mag. Reson. Med. 16, 3642, 2008.

3. V. Rasche, R. Proksa, P. Bornert and H. Eggers. Resampling of data between arbitrary grids using convolution interpolation. IEEE Trans Med Imaging. 18, 385-392, 1999.

Figures

Plot of the final trajectory, generated using a Sobol base-2 low-discrepancy sequence. The trajectory consists exemplary of twenty-thousand points within unit and spherical $$$k$$$-space and a backfolding of 20 % of all points to account for the necessary centre-oversampling.

Comparison of the normalized gradient amplitudes with respect to the index of the point-set of the trajectory for the unsorted (a) and the sorted trajectory (b). For each plot 500 three-dimensional point sets were used, corresponding to an exemplary reconstruction matrix size of eight. For the creation of the sorted trajectory, the sphere was divided into nine slices.

Depiction of the Delaunay triangulation in a) and the corresponding Voronoi tessellation in b) for an arbitrary two-dimensional set of points. The Voronoi space is unbounded and therefore the area of all outer cells is infinite. All inner points within a grey cell can be weighted using the respective cell area in $$$k$$$-space.

Sagittal plane of a mouse femur, penetrated with a titanium pin. The figure compares the SPI images acquired using the described trajectory with the eight-fold undersampled counterpart that is once enhanced using Compressed Sensing. A ZTE is shown for comparison of the metal artefact extension within the tissue. Acquisition parameters for the fully sampled SPI image were set to: $$$N=128$$$, $$$FOV = 35$$$ mm (isotropic), $$$T_\text{Rep} = 1.2$$$ ms, $$$t_\text{Echo} = 127$$$ $$$\mu$$$s and $$$\alpha = 1^\circ$$$ and identical for the ZTE except $$$T_\text{Rep} = 3.5$$$ ms, $$$t_\text{Echo} = 5.7$$$ $$$\mu$$$s and $$$BW = 150$$$ kHz.

Coronal plane of a mouse femur, penetrated with a titanium pin. The figure compares the SPI-image, acquired using the described trajectory with the eight-fold undersampled counterpart, that is once enhanced using Compressed Sensing. A ZTE is shown for comparison of the metal artefact extension. Displayed is each an excerpt of the slice. Acquisition parameters for the fully sampled SPI image were set to: $$$N=128$$$, $$$FOV = 35$$$ mm (isotropic), $$$T_\text{Rep} = 1.2$$$ ms, $$$t_\text{Echo} = 127$$$ $$$\mu$$$s and $$$\alpha = 1^\circ$$$ and identical for the ZTE except $$$T_\text{Rep} = 3.5$$$ ms, $$$t_\text{Echo} = 5.7$$$ $$$\mu$$$s and $$$BW = 150$$$ kHz.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
4026