4021
Spiral keyhole imaging for MR fingerprinting1IMAGO7 Research Center, Pisa, Italy, 2IRCCS Stella Maris, Pisa, Italy, Pisa, Italy, 3Technische Universität München, Munich, Germany, 4GE Global Research, Munich, Germany
Synopsis
MR Fingerprinting can be used for a fast and quantitative estimation of physical parameters in MRI. For the fast acquisition of MRF, common approaches have used non-Cartesian sampling of k-space. Here, we introduce a method for non-iterative anti-aliasing of the spiral MRF time series, based on the concept of keyhole imaging. Our approach does not change acquisition or dictionary creation and matching procedures. As frames require only minimal density compensation in k-space, noise amplification during reconstruction is reduced. After applying our algorithm, individual images from the MRF time series are artifact-free and clearer parameter maps are obtained in a shorter time while preserving the accurate quantification of MRF.
Introduction
Magnetic resonance fingerprinting (MRF) is an efficient method to acquire quantitative parameters using MRI [1]. Fast acquisition of MRF data usually features non-Cartesian k-space sampling schemes, using variable density spirals [1,2] or radial waveforms [3]. With these strategies, sampling density is higher in areas rich of contrast information at the centre of k-space, while areas containing less image contrast, such as the edges of k-space, are sampled less frequently. One of the main advantages of MRF is that imaging frames do not require full sampling, as pattern matching can “see through” aliasing [1]. Although anti-aliasing is not required, it has been demonstrated that using anti-aliasing strategies on the imaging frames can permit higher acceleration [4,5]. Most approaches have used iterative algorithms, which come at the expense of long image reconstruction times. Recently, a non-iterative anti-aliasing scheme was demonstrated for MRF using Cartesian imaging for small animals at 4.7T, based on the concept of k-space view sharing [6]. Here, we extend this approach to spiral MRF of the human brain.Methods
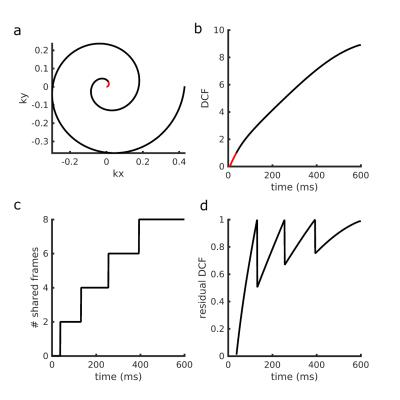
Our method is based on the concept of k-space view sharing. The original MRF approach applies density correction to the acquired k-space points and zero-filling to non-acquired datapoints. In our approach, k-space coordinates are first divided into two groups: oversampled part, where the k-space density compensation function (DCF) is less than 1, and the undersampled part, where the DCF is greater than 1 (Figure 1a). In the oversampled area, standard density compensation is applied (Figure 1b). In the undersampled area, each k-space point is shared with 2n neighbouring views. The number 2n approximates, for each k-space coordinate, the sampling density associated with the given distance to the k-space centre (Figure 1c). As this view-sharing step only accounts for odd integer DCF values, a small density correction factor is still applied to the borrowed data-points to achieve uniform sampling across all k-space points (Figure 1d).
MRF acquisition
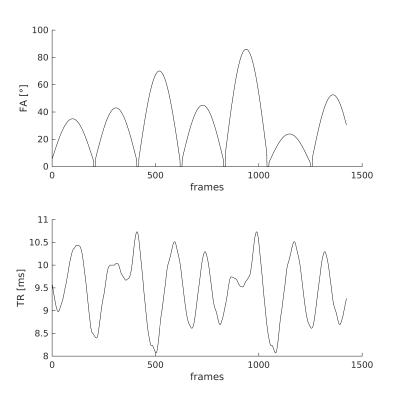
Data was acquired using a gradient-spoiled SSFP spiral MRF sequence at 1.5T (GE HDx, 8ch receiver coil, Milwaukee USA) [2]. Dictionary creation and pattern matching were as in [1], acquisition parameter list is shown in Figure 2. To maximize spatial and temporal incoherence, we incremented the angle of the spirals each time by the golden angle [7].
Conservation of quantification and acceleration
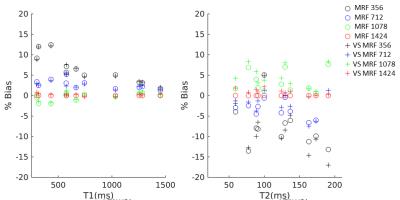
We scanned the Eurospin TO5 phantom [8], and retrospectively performed the MRF experiment using the first 356, 712, 1078, and 1424 frames. We compared quantification values across undersampling factors and between the keyhole approach and the standard reconstruction. To evaluate the method in a more realistic case, we acquired data in one asymptomatic volunteer.
Conservation of image geometry
To assess whether the described anti-aliasing technique would corrupt image geometry, we scanned a resolution phantom and compared the image when applying the algorithm and when not applying it. We used visual inspection for qualitative assessment and the autofocus objective function [9] averaged across the image as a quantitative metric of conservation of the PSF.
Results
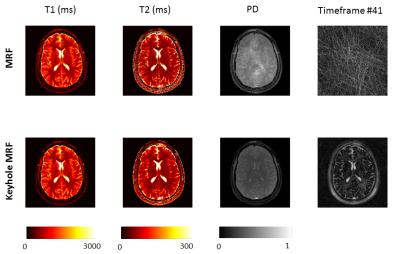
Figure 3 shows the effects on quantification of shortening the MRF acquisition, with and without our anti-aliasing strategy. Shortening acquisition achieved similar bias (<5% for T1 in 712 frames, <10% for T2 when acquiring 712 frames) in both cases, indicating that quantification is affected by acquisition length but not by anti-aliasing. Figure 4 displays brain images obtained with the first 754 frames only. Our anti-aliasing technique can achieve clearer T1, T2 and PD maps without increasing scan time, as well as giving diagnostically useful un-aliased frames. Figure 5 shows the effects of view sharing on a geometrical phantom, showing that image geometry is conserved when using our algorithm.Discussion
Our results demonstrate anti-aliasing of MRF frames without using iterative algorithms. The concept used is similar to keyhole imaging [10], and is based on the assumption that the image contrast is mainly stored in the centre of k-space, while the image details, which are mostly unchanged between frames, are in the edges of k-space. Therefore, the signal evolution for dynamic imaging can be in principle estimated well when only the central part of k-space is updated between subsequent frames. Notably, our approach requires only minimal density compensation in k-space, leading to less noise amplification. As the anti-aliased frames are free from artefacts, these can be used for radiological purposes in addition to the parameter maps.Conclusion
We demonstrated keyhole spiral MRF. Our algorithm achieves significant acceleration with a preservation of the accurate quantification of MRF and does not require iterative algorithms or changes to the dictionary.Acknowledgements
No acknowledgement found.References
[1]Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, et al. Magnetic resonance fingerprinting. Nature 2013;495:187–192. doi:10.1038/nature11971.
[2]Jiang Y, Ma D, Seiberlich N, Gulani V, Griswold MA. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn Reson Med 2014;74:1621–1631. doi:10.1002/mrm.25559.
[3]Cloos MA, Knoll F, Zhao T, Block KT, Bruno M, Wiggins GC, et al. Multiparametric imaging with heterogeneous radiofrequency fields. Nat Commun 2016;7:12445. doi:10.1038/ncomms12445.
[4] Davies M, Puy G, Vandergheynst P, Wiaux Y. A compressed sensing framework for magnetic resonance fingerprinting. Siam J Imaging Sci 2014;7:2623–2656. 6. Wang Z, Zhang Q, Yuan J, Wang
[5]B. Zhao, K. Setsompop, B. Gagoski, H. Ye, E. Adalsteinsson, P. E. Grant, and L. L. Wald, “A Model-Based Approach to Accelerated Magnetic Resonance Fingerprinting Time Series Reconstruction,” Proc Intl Soc Mag Reson Med, 2016.
[6]Buonincontri G, Sawiak SJ. MR fingerprinting with simultaneous B1 estimation. Magn Reson Med 2015. doi:10.1002/mrm.26009.
[7]Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the Golden Ratio for time-resolved MRI. IEEE Trans Med Imaging 2007;26:68–76. doi:10.1109/TMI.2006.885337.
[8]Man LC, Pauly JM, Macovski A. Improved automatic off-resonance correction without a field map in spiral imaging. Magn Res Med 1997; 37: 906–913.
[9]Lerski RA, de Certaines JD. Performance assessment and quality control in MRI by Eurospin test objects and protocols. Magn Reson Imaging 1993;11:817–833.
[10] van Vaals JJ, Brummer ME, Dixon WT, Tuithof HH, Engels H, Nelson RC, Gerety BM, Chezmar JL, den Boer JA. “Keyhole” method for accelerating imaging of contrast agent uptake. J Magn Reson Imaging1993;3:671–675.
Figures