Synopsis

A design consideration for center-out k-space trajectories is the angular distribution of trajectory endpoints (or equivalently, exit angles). Uniformity is desirable, but the regularity of spacing affects aliasing patterns, which can dictate undersampling performance. Here, a method for choosing points on a sphere with Poisson disc spacing is described, and its use in selecting angles for a 3D radial UTE sequence is validated.

Purpose / Motivation

Sampling three-dimensional $$$k$$$-space along center-out paths incurs intrinsic encoding inhomogeneity, as every path starts at $$$k=0$$$. Center-out $$$k$$$-space MRI sequences include UTE and ZTE^[1–3]; both typically traverse radial-spoke paths. Center-out sampling has two primary consequences. One is that, particularly for radii/spokes, acceptable image quality requires many sample-path acquisitions, with Nyquist-sampling non-uniformly satisfied and SNR efficiency diminished^[4]. Another is that uniformly distributing acquisition samples is nontrivial, but acquisitions traversing spokes to a surface $$$S$$$, e.g., a sphere, maximize sample-efficiency with endpoints distributed maximally-uniformly over $$$S$$$. Intuitively the desired points-set maximizes net inter-point distance, but this and similar formulations are non-convex, with mostly non-obvious solutions^[5]. Absent known globally-optimal distributions, heuristic spherical-surface point-drawing methods yielding relative uniformity are used^[6–8].

Here, a new approach is proposed, randomly drawing points on a spherical surface with Poisson disc distance distribution. It develops similar distribution uniformity, while also rendering incoherent aliasing patterns. Incoherence/randomness eases sampling requirements, making benign degradation in image quality with increasing undersampling rate. Additionally, it conditions data for sparsity-assuming (compressed-sensing) reconstructions^[9].

Methods

Algorithms for picking points randomly with Poisson disc characteristics typically are formulated for some Cartesian-coordinate bounded region of $$$\mathbb{R}^{n}$$$^[10] and can be efficiently implemented (linear-time)^[11]. Such Poisson disc sampling formulations randomly draw coordinates from two region-types, which can be performed by transforming independent uniform-distribution variables, $$$\{u_i\sim\textrm{unif(0,1)}\}_i$$$. These algorithms have as parameters exclusion/inclusion radii $$$r_{e1}$$$/$$$r_{e2}$$$.

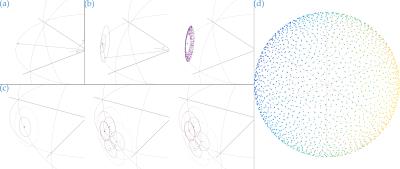
Here, to pick points on a radius-$$$r_s$$$ sphere in $$$\mathbb{R}^{3}$$$ with Poisson disc distribution, the random-number-generation steps of a Cartesian algorithm^[11] are adapted. First, the seed is selected uniformly-randomly from the entire radius-$$$r_s$$$ surfaceas$$p_0=(r_s,\theta,\phi)\quad\textrm{with}\quad\theta=0+(2{\pi}-0){u_1}\;\textrm{and}\;\phi=\cos^{-1}(\cos0+(\cos\pi-\cos0)u_2)\textrm{,}$$(Fig.1a).Second, the iteration candidate-intermediates point-draw operation is modified to choose from a spherical patch within exclusion/inclusion distances (Fig.1b)like$$\begin{aligned}\tilde{q_1}=(r_s,\theta,\phi)\quad\textrm{with}\quad&\theta=2{\pi}u_1\textrm{,}\;\phi=\cos^{-1}(\cos\phi_1+(\cos\phi_2-\cos\phi_1)u_2)\\&\textrm{and}\;\phi_{1,2}=\cos^{-1}(1-r_{e1,2}^2/(2r_s^2))\end{aligned}$$(Fig.1b,c).With seed- and candidate-drawing updated, all points necessarily lie on the sphere. Stopping conditions remain unchanged. Completing iterations provides a random set of Poisson disc-spaced points maximally covering the surface (Fig.1d).

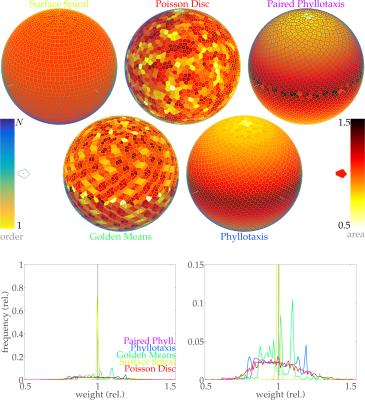
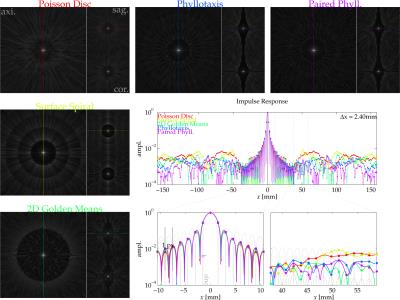
Performance validations imaging with Poisson disc-random $$$k$$$-space radial endpoints were undertaken through comparison with surface-spiral^[6], golden-means^[7], spiral-phyllotaxis^[8] patterns. All patterns drew 3177 points (Fig.2), undersampling angular dimensions to illustrate aliasing characteristics. For the variety of point-drawing methods, impulse responses were simulated with a representative $$$k$$$-space-radial trajectory encoding 212$$$^{\textrm{3}}$$$-voxel fields-of-view (Fig.3). Simulations computed gridding-Fourier transforms of synthetic impulse data (ones in $$$k$$$-space) with angular-density-compensation weights derived by Voronoi tilings (Fig.2). Along central cross-sections, responses were sinc-interpolated for finer depiction of resolution/aliasing. The spherical-$$$k$$$-space-coverage impulse function^[12] $$$h$$$ is plotted for reference (Fig.3).

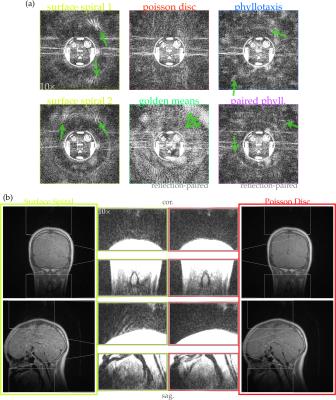
MRI experiments were also undertaken with the point constellations. For comprehensive comparative evaluation, a phantom was imaged by 3D UTE center-out radial acquisition encoding with $$$k$$$-space endpoints from six different patterns (Fig.4a). Phantom acquisition parameters include 250kHz bandwidth/244$$$^{\textrm{3}}$$$ voxels/(30cm)$$$^{\textrm{3}}$$$ field-of-view/15761 spokes (11.9$$$\times$$$-undersampled)/15$$$^{\circ}$$$ tip/36μs TE/5.4ms TR/1.5T scanner/transmit-receive head coil.

To demonstrate realistic clinical performance, a healthy subject head was also imaged using surface-spiral or spherical-surface Poisson disc endpoints (Fig.4b). In vivo acquisition parameters include 250kHz bandwidth/244$$$^{\textrm{3}}$$$ voxels/(28cm)$$$^{\textrm{3}}$$$ field-of-view/47061 spokes (4$$$\times$$$-undersampled)/12$$$^{\circ}$$$ tip/34μs TE/6.2ms TR/3T scanner/eight-channel-receive head coil.

Results

Poisson disc random points for 3D radial $$$k$$$-space trajectories reduce aliasing coherence relative surface-spiral, golden-means, and spiral-phyllotaxis patterns (Fig.3). Response smoothness outside the undersampling-reduced field-of-view evidences the reduction (Fig.3).

Image quality in gridding/DFT reconstructions of undersampled phantom acquisitions improves with more benign aliasing (Fig.4a). Phantom images demonstrate this clearly: coherent streak-aliasing encircles the phantom encoded by all methods except Poisson disc-chosen endpoints. Perceptively, this improves image quality when aliasing may overlap the object, e.g., for in vivo imaging (Fig.4b).

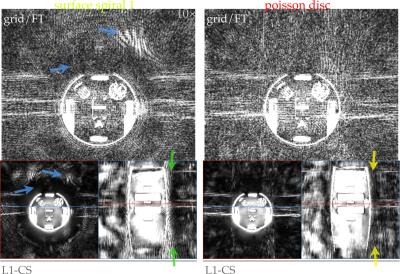
Beyond improving image quality, Poisson disc endpoints-selection conditions data for sparsity-assuming image reconstructions. Reconstruction by $$$\ell1$$$-norm-regularized compressed sensing from surface-spiral data yields unresolved streak-aliasing, while that from Poisson disc-endpoints data does not (Fig.5).

Discussion and Conclusions

Poisson disc-random sampling picks points a sphere with relatively uniform inter-point spacing. It sacrifices positioning-uniformity as compared to idealized spacing, which surface-spiral-drawn points nearly achieve. However, in practical imaging scenarios, reduced aliasing coherence outweighs uniformity-diminution of Poisson disc-selected points.

Reconstructing 3D radial-$$$k$$$-space-encoded images by gridding/DFT is sometimes appealing, with predictable artifacts. Image quality degrades gradually under sample-count reductions. However, radial-$$$k$$$-space-characteristic streak-aliasing can be disruptive if intense. Aliasing intruding upon signal voids (e.g., air) is particularly confounding for, e.g., ZTE-derived PET attenuation correction^[13], in which distinguishing signal-absent air from hypointense bone is crucial.

Compressed-sensing reconstruction performs well with randomly-distributed samples. The sample-location distribution affects reconstructed image quality, however, and Poisson disc-spacing eases reconstruction demands^[14,15]. While radially-sampled $$$k$$$-space is fairly compatible with compressed sensing^[15,16], sampling a regularly-spaced angular distribution of spokes reduces incoherence, hampering leveraging sparsity assumptions. Poisson disc-random angle-picking creates favorable conditions for sparsity-assumed reconstructions by reducing coherent streaking. This extends the boundary of practicable undersampling ratios for center-out MRI.

Acknowledgements

References

[1] Rahmer, J., Börnert, P., Groen, J., & Bos, C. (2006). Three-dimensional radial ultrashort echo-time imaging with T2 adapted sampling. Magnetic resonance in medicine, 55(5), 1075-1082.

[2] Madio, D. P., & Lowe, I. J. (1995). Ultra-fast imaging using low flip angles and fids. Magnetic resonance in medicine, 34(4), 525-529.

[3] Weiger, M., Pruessmann, K. P., & Hennel, F. (2011). MRI with zero echo time: hard versus sweep pulse excitation. Magnetic resonance in medicine, 66(2), 379-389.

[4] Liao, J. R., Pauly, J. M., Brosnan, T. J., & Pelc, N. J. (1997). Reduction of motion artifacts in cine MRI using variable-density spiral trajectories. Magnetic resonance in medicine, 37(4), 569-575.

[5] Saff, E. B., & Kuijlaars, A. B. (1997). Distributing many points on a sphere. The mathematical intelligencer, 19(1), 5-11.

[6] Wong, S. T., & Roos, M. S. (1994). A strategy for sampling on a sphere applied to 3D selective RF pulse design. Magnetic Resonance in Medicine, 32(6), 778-784.

[7] Chan, R. W., Ramsay, E. A., Cunningham, C. H., & Plewes, D. B. (2009). Temporal stability of adaptive 3D radial MRI using multidimensional golden means. Magnetic resonance in medicine, 61(2), 354-363.

[8] Piccini, D., Littmann, A., Nielles-Vallespin, S., & Zenge, M. O. (2011). Spiral phyllotaxis: the natural way to construct a 3D radial trajectory in MRI. Magnetic resonance in medicine, 66(4), 1049-1056.

[9] Lustig, M., Donoho, D., & Pauly, J. M. (2007). Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic resonance in medicine, 58(6), 1182-1195.

[10] Mitchell, D. P. (1991, July). Spectrally optimal sampling for distribution ray tracing. In ACM SIGGRAPH Computer Graphics (Vol. 25, No. 4, pp. 157-164). ACM.

[11] Bridson, R. (2007, August). Fast Poisson disk sampling in arbitrary dimensions. In SIGGRAPH sketches (p. 22).

[12] Vembu, S. (1961). Fourier transformation of the n-dimensional radial delta function. The Quarterly Journal of Mathematics, 12(1), 165-168.

[13] Wiesinger, F., Sacolick, L. I., Menini, A., Kaushik, S. S., Ahn, S., Veit-Haibach, P., ... & Shanbhag, D. D. (2016). Zero TE MR bone imaging in the head. Magnetic resonance in medicine, 75(1), 107-114.

[14] Nayak, K. S., & Nishimura, D. G. (1998, April). Randomized trajectories for reduced aliasing artifact. In Proceedings of the 6th Annual Meeting of ISMRM, Sydney, Australia (p. 670).

[15] Lustig, M., Alley, M., Vasanawala, S., Donoho, D. L., & Pauly, J. M. (2009, April). L1 SPIR-iT: autocalibrating parallel imaging compressed sensing. In Proc Intl Soc Mag Reson Med (Vol. 17, p. 379).

[16] Jiang, W., Ong, F., Henry, R., Lustig M., & Larson P. E. Z. (2015, April). L1-ESPIRiT Reconstruction for Accelerating 3D UTE and Denoising. In Proceedings of the 23rd Annual Meeting of ISMRM, Toronto, Canada (p. 2449).