4015
Partial Fourier Shells Trajectory with Non-Iterative Homodyne Reconstruction1Radiology, Mayo Clinic, Rochester, MN, United States
Synopsis
The 3D Shells trajectory-based MRI acquisition is a non-Cartesian acquisition technique that divides the 3D k-space into a series of concentric shells and samples each one with 3D helical readouts. Using the Shells trajectory, the inner k-space can be efficiently sampled within several interleaves, making it a maximally centric 3D acquisition. Partial Fourier (PF) acquisition is a commonly-used acceleration technique by exploiting the conjugate symmetry of k-space measurement. In this work, we present a new asymmetric 3D Shells trajectory design with PF acceleration to combine the advantages from both techniques, and develop a non-iterative homodyne reconstruction framework for it.
Purpose
The 3D Shells trajectory divides the 3D k-space into a series of concentric shells and samples each one using 3D helical readouts1,2. With the Shells trajectory, the inner k-space, which determines the image contrast, can be efficiently sampled within several interleaves, making it a maximally centric 3D acquisition. The acquisition of inner shells can be synchronized with the time when a certain desired image contrast is expected, such as the contrast agent arrival time in gadolinium-enhanced MR angiography1, or when the peak of white-to-gray-matter contrast is achieved after a magnetization-preparation (MP) pulse3,4. Partial Fourier (PF) homodyne acquisition is a commonly-used acceleration technique in Cartesian MRI by exploiting the conjugate symmetry of k-space measurement5. However, unlike Cartesian MRI, utilizing homodyne acquisition in non-Cartesian acquisition is not straightforward, since directly applying homodyne acquisition in a direction sampled with non-Cartesian trajectory does not always yield a physically-achievable trajectory (e.g., 2D spiral)6, or an iterative reconstruction may be required7,8. Here, we present a new asymmetric 3D Shells trajectory design, and develop a non-iterative PF reconstruction for it.Methods
The 3D k-space shells with a radius of $$$k_r(n)=n\Delta$$$$$$k_r$$$ can be sampled using a series of 3D helical readouts expressed as: $$$k_z=k_r(n)\cos(\pi\tau/T)$$$, $$$k_x=k_r(n)\sin(\pi\tau/T)\cos(\omega_n\tau/T+\theta_{n,m})$$$, $$$k_y=k_r(n)\sin(\pi\tau/T)\cos(\omega_n\tau/T+\theta_{n,m})$$$, where $$$T$$$ is the total number of samples per readout, $$$\tau(\kappa)$$$ indices each readout sample, $$$\theta_{n,m}=\frac{2m\pi}{M(n)}$$$ is the initial phase of a interleave, $$$M(n)$$$ is the total interleave number, $$$m\leq$$$$$$M$$$ indices different interleaves, $$$\omega_n$$$ controls the rotational speed in k-space azimuthal direction. The gradient waveforms of each readout/interleave can be generated via a time-optimal waveform design strategy described by Lustig9. The gradient amplitude and slew rate limits are chosen to conform to both hardware limits and Nyquist sampling requirements10. The $$$\omega_n$$$ is iteratively determined so that each readout contains $$$T$$$ samples. The number of interleaves for each shell ($$$M$$$) is then calculated by constraining the maximal k-space distance (i.e., on the equator of each shell) between two adjacent interleaves to satisfy the Nyquist requirement, which yields $$$M=\lceil2\pi n\sin(\arctan(\pi/\omega_n))\rceil$$$. For a fully-sampled shells acquisition, $$$\tau\leq$$$$$$T$$$, and the trajectory samples the entire shell along z-direction (i.e. from $$$k_z=N\Delta k_r$$$ to $$$k_z=-N\Delta k_r$$$). To achieve PF acceleration, $$$\tau$$$ can be modified as $$$\tau=T/\pi\arccos((1-2\kappa)N/n)$$$, so that the trajectory only samples from $$$k_z=N\Delta$$$$$$k_r$$$ to $$$k_z=(1-2\kappa)N\Delta$$$$$$k_r$$$, where $$$\kappa$$$ denotes the PF factor ($$$0.5\leq\kappa\leq1$$$).
Assuming the proposed trajectory, the real-valued image vector, $$$\bf{u_r}$$$, can be reconstructed from the measured k-space data, $$$\bf{g}$$$, using a non-iterative gridding-type reconstruction5,11,12:
$$\bf{u_r}=\it{real}\bf{\{\Phi^*A^*D(\Psi_L+2\Psi_H)g\}} \it{(Eq.1)}$$
where $$$\bf{A}$$$ is the forward-encoding operator including off-resonance effects (presumed known from separate dual-echo prescan), and $$$\bf{A^*}$$$ its adjoint11,12. $$$\bf{D}$$$ is the sampling density compensation function determined for the Shells trajectory using Pipe and Menon’s algorithm13. $$$\bf{\Psi_L}$$$ and $$$\bf{\Psi_H}$$$ are binary diagonal matrices extracting the low-pass and high-pass regions of k-space along the PF acceleration direction (i.e., z). $$$\bf{\Phi}$$$ is a diagonal matrix that approximates the residual spatial phase signal (e.g., from eddy-currents, B1- fields) not considered within $$$\bf{A}$$$, which is estimated from the fully-sampled (z-direction), low-pass k-space data5. Note that Eq. 1 is applicable to Shells trajectory because one k-space hemisphere is fully sampled, based on our design.
As a test, the ACR phantom was scanned using both the fully-sampled and PF-accelerated (PF factor=0.7/0.6) Shells (Table 1). The brain of a healthy volunteer was also scanned under an IRB-approved protocol, using magnetization-prepared shells (MP-Shells) acquisitions3 and MPRAGE with matching parameters (Table 1). In MP-Shells, a series of Shell readouts are played following a center-out view-ordering after a MP module, i.e., the inner-most shells are acquired at inversion time (TI), followed by outer shells. The images were reconstructed (coil-by-coil) using a type-III NUFFT-based reconstruction with simultaneous (time-segmented) off-resonance and gradient-nonlinearity correction14, and sum-of-square combined post-reconstruction. Fat saturation was enabled in MP-Shells to suppress fat-induced blurring.
Results and Discussion
Figure1 shows an example of the fully-sampled (a) and PF-accelerated (factor=0.7) Shells trajectory (b; see captions). Figure 2 shows phantom images reconstructed from fully-sampled (a) or PF-accelerated Shells using the proposed (b/c) and zero-filling (d/e) reconstruction. Comparing with the fully-sampled case, the proposed PF-acquisition and reconstruction preserves image resolution while reducing acquisition time (Table 1). Figure 3 compares two PF Shells designs with different readout lengths showing reduced off-resonance effect with shorter readout (see captions). Figure 4 compares the MP-Shells images with MPRAGE. Note the improved white-matter-to-gray-matter-contrast in MP-Shells from acquiring the entire 3D k-space center shells at desired TI time.Conclusion
We developed a 3D Shells trajectory with PF-acceleration and a non-iterative homodyne reconstruction for it. This trajectory inherits the high k-space sampling efficiency from fully-sampled Shells but reduces acquisition time or sensitivity to off-resonance.Acknowledgements
This work was supported in part by the NIH grant R01EB010065.References
1. Shu Y, Bernstein MA, Huston J, Rettmann D. Contrast-enhanced intracranial magnetic resonance angiography with a spherical shells trajectory and online gridding reconstruction. J Magn Reson Med 2009;30:1101-1109.
2. Zahneisen B, Hugger T, Lee KJ, LeVan P, Reisert M, Lee HL, Asslander J, Zaitsev M, Hennig J. Single shot concentric shells trajectories for ultra fast fMRI. Magn Reson Med 2012; 68:484-494.
3. Shu Y, Tao S, Trzasko JD, Huston J 3rd, Weavers PT, Bernstein MA. Magnetization-prepared shells trajectory with automated gradient waveform design. Med Physics 2016;43:WE-FG-206-1.
4. Mugler JP 3rd, Brookeman JR. Three-dimensional magnetization-prepared rapid gradient-echo imaging (3D MP RAGE). Magn Reson Med 1990;15:152-157.
5. Noll DC, Nishimura DG, Macovski A. Homodyne detection in magnetic resonance imaging. IEEE Trans Med Imaging 1991;10:154–163.
6. Block KT, Frahm J. Spiral imaging: a critical appraisal. J Magn Reson Imaging 2005;21:657-668.
7. Moriguchi H, Lewin JS, Duerk JL. Partial Fourier spiral reconstruction under consideration of off-resonance effects. In Proceedings of the 12th Annual Meeting of the ISMRM, Kyoto, Japan, 2004. p.346.
8. Lee JH, Pauly JM, Nishimura DG . Partial k-space reconstruction for radial k-space trajectories in magnetic resonance imaging. US patent 7,277,597. 2003.
9. Lustig M, Kim SJ, Pauly JM. A fast method for designing time-optimal gradient waveforms for arbitrary k-space trajectories. IEEE Trans Med Imaging 2008;27(6):866-873.
10. Shu Y, Riederer SJ, Bernstein MA. Three-dimensional MRI with an undersampled spherical shells trajectory. Magn Reson Med 2006;56:553-562.
11. Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using minmax interpolation. IEEE Trans Signal Process 2003;51:560–574. 12. Beatty PJ, Nishimura DG, Pauly JM. Rapid gridding reconstruction with a minimal oversampling ratio. IEEE Trans Med Imaging 2005;24:799–808.
13. Pipe JG, Menon P. Sampling density compensation in MRI: rationale and an iterative numerical solution. Magn Reson Med 1999;41:179-186.
14. Tao S, Trzasko JD, Shu Y,
Huston J 3rd, Johnson KM, Weavers PT, Gray EM, Bernstein MA. NonCartesian MR
image reconstruction with integrated gradient nonlinearity correction. Med Phys
2015;42:7190– 7201.
Figures
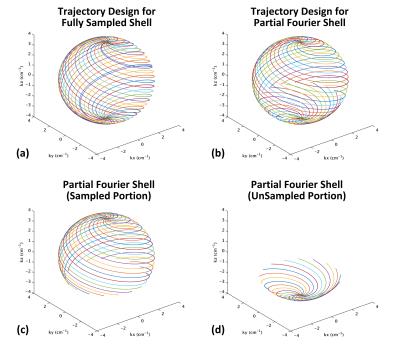
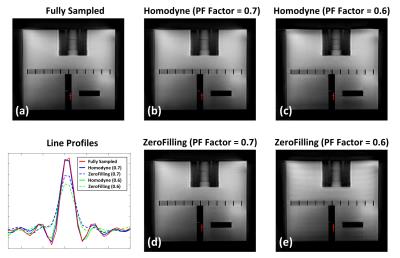
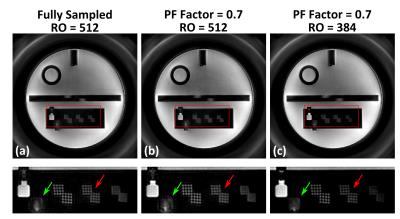

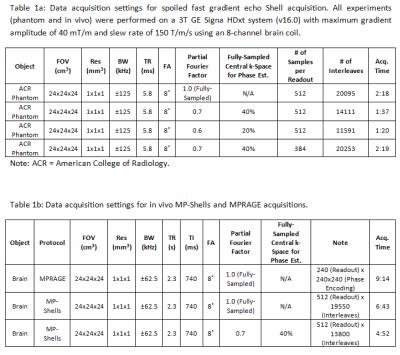
Table 1a: Data acquisition settings for spoiled fast gradient echo Shells acquisition. All experiments (phantom and in vivo) were performed on a 3T GE Signa HDxt system (v16.0) with maximum gradient amplitude of 40 mT/m and slew rate of 150 T/m/s using an 8-channel brain coil.
1b: Data acquisition settings for in vivo MP-Shells and MPRAGE acquisitions.