Purpose

Radial imaging employing Golden Angle¹ angle increments is a popular research topic due to the high degree of flexibility in the reconstruction process after data acquisition. This flexibility may improve, e.g., cardiac real-time imaging in challenging situations where standard Cartesian cine sequences fail. However, when switching from standard Cartesian to radial sequences, usually streaking artifacts are a challenge. The origin of these artifacts is manifold and minimizing these influences is of course important to lower the artifact energy of these. Nonetheless, techniques to deal with remaining streaking artifacts have been discussed in earlier publications². An interesting method in this context is the truncated principal component analysis (PCA) or Karhunen-Loeve transform (KLT)^3,4. Especially when the positions of the streaking artifacts change from temporal frame to frame, the KLT can be very helpful to remove streaking artifacts while simultaneously improving the apparent SNR of the dataset. A challenge in this context is the proper selection of the truncation of the principal components (PC). If too many PCs are discarded, a phenomenon similar to temporal blurring can be observed. If too many PCs are maintained, streaking may still be too prominent. We suggest using the L₁ energy of the PC eigenvalues as an indicator how many PCs to maintain. Furthermore, using a soft thresholding employing an exponentially decaying function may be considered instead of hard thresholding of the PCs. As we show, this method reduces temporal blurring, streaking artifacts, and improves apparent SNR in the timeframes.

Methods

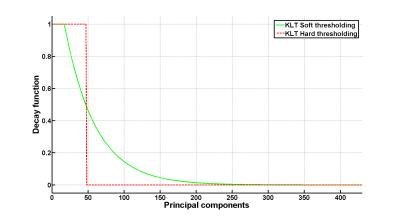
A radial bSSFP sequence was used to obtain data from a healthy volunteer on a 3.0T MRI scanner (MR750, GE Healthcare, Waukesha/WI, USA). All subsequent data processing was performed in Matlab (The MathWorks Inc., Natick, MA, USA). After reconstruction of a real-time dataset employing view sharing using a Tornado shaped temporal filter⁵ and subsequent iterative SENSE reconstruction⁶, these data were considered as ground truth. Next, the data were subject to KLT. Hereby, a regular hard thresholded KLT was compared to a soft thresholded KLT. Thresholding was performed such that 99.00,99.25,99.50, or 99.75% of the original L₁ energy of the PCs was maintained. Soft thresholding was performed using an exponential decay function exp(-x/DPC) where x is the vector with the PC eigenvalues and DPC is the decay constant and was set to 10% of the number of timeframes (see example in Fig.1). The thresholded KLTs were subtracted from the ground truth real-time dataset and visually compared. Furthermore, the L₁ norm of the absolute difference values between the KLTs and ground truth were calculated and plotted against the chosen threshold.

Results

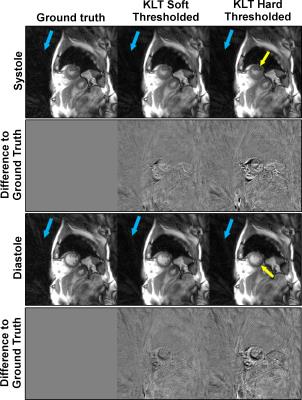
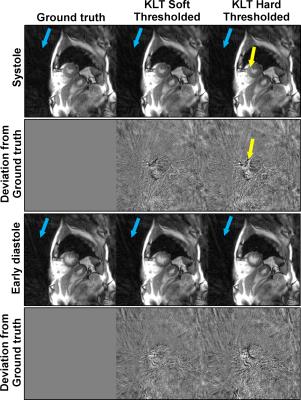
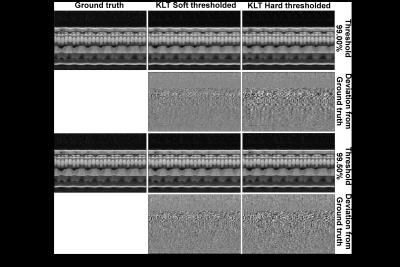
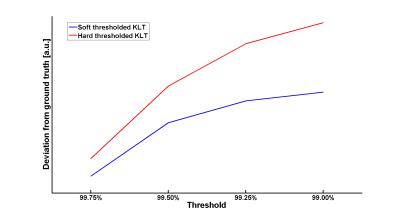
Fig. 2 and 3 compare the different KLT-thresholding strategies for thresholds 99.00% and 99.50%. As can be seen, for 99.00%, hard thresholding suffers from significantly reduced temporal accuracy while the proposed soft thresholding performs better (see yellow arrows). For 99.50%, there is almost no visual difference in the images. However, when looking into the difference images to the ground truth, advantages for soft thresholding can be seen. This impression is further confirmed by comparing the resulting time-courses at a representative profile through the heart (Fig. 4). Hard thresholding the PCs compromises the temporal fidelity while soft thresholding performs better. This is quantified in Fig. 5, where the L₁ norm of the absolute differences values between the thresholded KLTs and the ground truth clearly shows that soft thresholding maintains a better representation of the original dataset than hard thresholding.

Discussion & Conclusion

The presented idea to truncate the KLT in either a soft or hard way removes the operator dependency for selecting a proper threshold. By determining the minimum required PC information in the L₁ sense, the obtained real-time dataset does not suffer from temporal blurring which is of utmost clinical importance. Furthermore, the beneficial properties of the KLT – streaking reduction and improved apparent SNR – are maintained. In the presented example, 99.5% of the initial L₁ energy of the PC eigenvalues was found to be a good threshold to balance minimal streaking against temporal accuracy. Please note, even though the image quality of soft and hard thresholding for 99.50% is almost indistinguishable, that hard thresholding introduces subtle errors and deviations from the original dataset (see Fig. 4 and 5). These differences could become critical in situations where slight signal intensity variations in the myocardium are of clinical relevance, e.g. in myocardial edema⁷. More volunteer and patient datasets are required to establish a robust threshold for the proposed technique. Also, the decay constant could be further optimized. In general, the threshold should be well-balanced between streaking artifact removal and temporal accuracy.