4006
Rapid 3D imaging with multiplanar spiralsMaria Engel1, Lars Kasper1, and Klaas Paul Pruessmann1
1ETH, Zürich, Switzerland
Synopsis
Rapid 3D acquisition with long spiral readouts is enabled by multiplanar undersampling, array detection and an expanded signal model including off-resonance. Whole brain coverage with 1.5 mm isotropic resolution is achieved in 3.1 s.
Introduction
3D Fourier encoding is a particularly SNR efficient scanning strategy. It acquires data from the entire volume and is amenable to optimal (3D) undersampling. This sensitivity gain can be invested in faster scans (quick and inexpensive clinical exams), higher spatial- (structural imaging) and temporal resolution (fMRI) [1]. Amongst the 3D techniques, 3D spiral trajectories provide a particularly beneficial way of covering k-space: they optimally exploit gradient system (slew-rate) performance and provide naturally optimized k-space coverage and weighting. Currently, spiral imaging usually suffers from severe artefacts, as dynamic encoding imperfections and static field inhomogeneities translate into blurring and distortions. In this work, these obstacles are overcome by drawing on a comprehensive encoding model. The iterative conjugate gradient SENSE reconstruction algorithm [2], including multifrequency interpolation [3, 4] for static off-resonance correction and concurrently monitored encoding field dynamics [5], was extended to three dimensions and applied to T2*-weighted gradient echo sequences with multiplanar stacks of spirals.Methods
Hardware: All experiments were performed on a Philips 7T Achieva system using a 32 channel head array (Nova Medical). 16 NMR field probes were mounted on the head array and their signals were acquired using a dedicated MR acquisition system [6] during all sequences. From this data the actual encoding fields up to 2nd order in space were calculated. Sequence: Aiming for whole brain coverage, a slab of 10cm thickness was excited and the readout started at TE=20ms in order to generate T2*-contrast. K-space was covered by a stack of Archimedean spiral out trajectories, FOV 23x23x12cm3, thus accounting for potential sidebands of the excitation pulse shape. Acquiring interleaves of 32ms duration and applying a total undersampling factor of 4, 1.1mm isotropic resolution could be reached in 7.7 seconds. In order to facilitate unfolding for parallel imaging, spiral interleaves were arranged on a hexagonal grid in slab direction [7]. In a second implementation, an accelerated scan was performed by introducing gradient blips after each full rotation [8], that way covering two k-space planes within one shot (Figure 2) and covering an identical FOV in 3.1seconds with 1.5mm isotropic resolution. Image reconstruction: The images were reconstructed using an iterative conjugate gradient SENSE reconstruction algorithm [2] extended to 3D, including multifrequency interpolation [3, 4] for static off-resonance correction and based on the concurrently monitored encoding field dynamics [5] of 0th and 1st spatial order. Off-resonance and coil sensitivity maps were computed from a multiecho, multisclice spin-warp pre-scan (6 echoes, TE 4-9ms, 1x1x3mm resolution).Results
The isotropic 1.1mm stack-of-spiral scan (Fig. 1) exhibits decent T2*-contrast and SNR and shows appealing spiral image quality. The challenging multiplanar spiral trajectory induces significant eddy currents, such that the image reconstruction requires the input of the actual dynamic encoding. This can be seen in Figure 3, comparing image reconstructions based on encoding models of different complexity. Fig. 2 shows the monitored k-space evolution of 0th, 1st and 2nd order.Discussion
An SNR efficient, accelerated 3D spiral method for fast whole brain MR imaging was presented. It circumvents many intricacies that are introduced by alternatives such as multiband imaging with its advanced sampling schemes and SAR moderate RF pulse design. A key factor for appealing 3D spiral image quality is the consideration of all relevant dynamic and static encoding field terms: static off-resonance, gradient field dynamics (0th and 1st order) including all delays and coupling terms, as well as coil sensitivities. By measuring and concurrently monitoring these fields and feeding them into the signal model, high quality spiral images can be reconstructed. In 3D scans, which enforce multiple shots, concurrent field monitoring becomes even more crucial, being sensitive also to inter-shot dynamics. The SNR gain from robust 3D spiral imaging at ultra-high field will benefit a number of applications, amongst them being BOLD-fMRI, ASL as well as high-resolution structural imaging.Acknowledgements
No acknowledgement found.References
[1] B. A. Poser et al., NeuroImage 51.1 (2010): 261–266 [2] K. Prüssmann et al., Magnetic Resonance in Medicine (2001), 46: 638-651 [3] L.C. Man, et al., Magnetic Resonance in Medicine (1997), 37: 785–792. [4] C. Barmet et al., Proc. Intl. Soc. Mag. Reson. Med. 23 (2005), 682 [5] C. Barmet et al., Proc. Intl. Soc. Mag. Reson. Med. (2010), 216 [6] B. Dietrich et al., Magnetic Resonance in Medicine, 2015, Epub ahead of print, 1-10 [7] R. M. Mersereau, Proceedings of the IEEE (1979), 67: 930-949 [8] B. Zahneisen et al., Magnetic Resonance in Medicine (2014), 71: 2071-2081Figures

Images acquired by a stack of Archimedean spiral out trajectories. Images
were reconstructed by conjugate gradient iterative SENSE reconstruction with
reduction factor 4. Three transversal, a coronal and a sagittal view of a 10cm
thick slab are shown. FOV 23x23x12cm3, 1.1mm isotropic resolution, TE=20ms,
undersampling factor 4, matrix size 190x230x100.
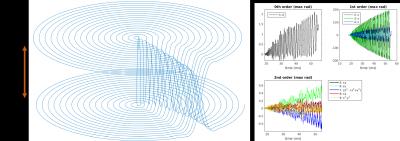
One
interleaf of the (nominal) blipped spiral trajectory is shown in parametric
representation (in kz-direction the plot is stretched for improved orientation).
The monitored time courses of the spherical harmonic phase evolution in 0th,
1st and 2nd order are plotted versus time.
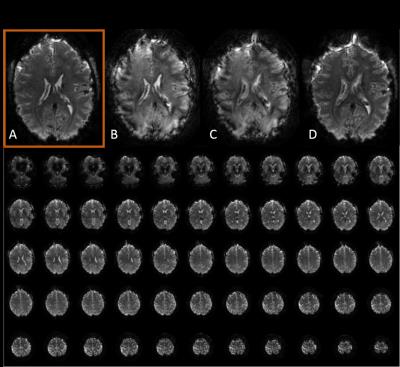
Images
acquired with a stack of spirals, where each shot covers two k-space planes,
with blips switching between planes after every spiral turn (Figure2). In the
upper row the impact of the different contributions to the comprehensive signal
model are visible: A)reconstruction using the comprehensive signal model,
including off-resonance correction, monitored field dynamics (0th,1st order),B)image reconstructed on the nominal trajectory including
off-resonance correction,C)image reconstruction without off-resonance
correction, using the nominal k-trajectory,D)image reconstructed on the
monitored-trajectory, but in the absence of off-resonance correction. In the
lower panel the most important slices are shown, reconstructed corresponding to
the method used in d)