Synopsis

3D-FFT via gridding is generally recognized as computationally faster than direct 3D filtered backprojection (FBP) in 3D radial-data reconstruction. To overcome the computational time issue of 3D-FBP, we investigated two-step 2D-FBP reconstruction having an alternative k-space trajectory. Computational requirements were theoretically analyzed to permit clear comparison among three reconstruction methods and computational burdens based on mathematical expressions were compared to actual computation times. In conclusion, two-step FBP provides considerable computational speed benefit over direct 3D-FBP and, under certain realistic conditions (e.g., with many channels), even over 3D-FFT, while showing almost same image quality in phantom and brain imaging.

Purpose

Methods

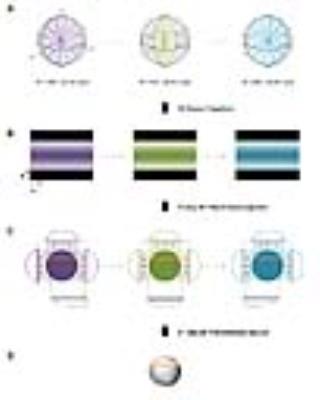
Two-Step FBP Algorithm: To apply tsFBP algorithm, partial gradient echoes were radially collected filling a disc in k-space by incrementing θ (0≤θ<2π) for a given ∅ (Fig.1A) with an acquisition scheme of CODE(Concurrent Dephasing and Excitation)⁵, which was repeated for a set of equally spaced ∅ in the range of 0≤∅<π. Following data acquisition, a set of 1D projections (or sinograms) were obtained by 1D FFT at each ∅ (Fig.1B). Then, a stack of ∅-dependent 2D projection images (colored discs in Fig.1C) were obtained by 2D FBP from each sinogram. Final 3D image was obtained by a series of 2D FBP using z-coordinate-matched yellow strips of the 2D projection images in the previous step (Fig.1D).

Computation: To compare the computational requirements, the number of operations was calculated, considering the major computational parts of each method. Detailed part-by-part operational counts and parameters are listed in Table 1.

tsFBP can be divided into three main steps such as 1D FFT, 1^st-step FBP, and 2^nd-step FBP, and, summing up, the number of tsFBP operations is,

$$O_{tsFBP}=N_{view}(N_{s}log_{2}N_{s})N_{ch}+(N_{view,\theta}N_{x}N_{y})N_{view,\phi}+(N_{view,\phi}N_{x}N_{y})N_{z}. [1]$$

dFBP mainly consists of 1D FFT and 3D FBP, whose number of total operations is given by,

$$O_{dFBP}=N_{view}(N_{s}log_{2}N_{s})N_{ch}+(N_{x}N_{y}N_{z})N_{view}. [2]$$

For gFFT, three main steps such as gridding, 3D FFT, and intensity correction were counted⁶ and, as a total,

$$O_{gFFT}=[N_{view}N_{s}\omega^{3}+V^{3}N_{x}N_{y}N_{z}log_{2}(V^{3}N_{x}N_{y}N_{z})+N_{x}N_{y}N_{z}]N_{ch}. [3]$$

For comparison of each method, number of operations were calculated using Eqs.[1-3] with N_view=4π(N_s)² satisfying Nyquist criterion, V=1.375, and ω=5, with respect to final matrix size varying number of channels. To draw a comparison between computational burden and actual computational time and to confirm image quality, an ACR phantom and the human brain were scanned at 3T (Siemens Trio) using a 4-channel volume coil. Image reconstruction was performed offline using a home-built MATLAB (ver.8.2.0; R2013b) program on a workstation equipped with an Intel-Xeon CPU (3.50GHz processor) and an NVIDIA Quadro K600 graphics card.

Results and Discussion

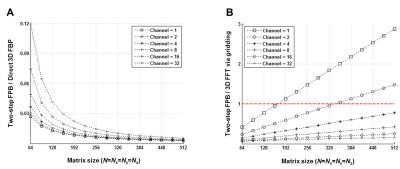
Figure 2 shows the ratios between the operational counts of tsFBP and the other two methods. Computational requirement was substantially reduced in tsFBP compared to dFBP (Fig.2A). tsFBP also has advantage over gFFT as the number of channels increases. Even with a small number of channels (≤ 2), tsFBP is still more efficient for a large final matrix size (e.g., > ~340 for 2 channels).

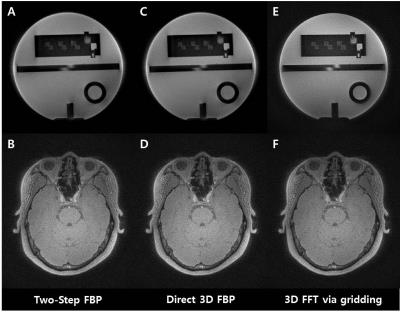
Figure 3 shows representative axial slices of the ACR phantom and the human brain reconstructed using tsFBP, dFBP, and gFFT. Image qualities were very comparable. In particular, images from tsFBP and dFBP are hardly distinguishable despite their very different reconstruction times. Table 1 shows the computational burdens for a theoretical example based on Eqs.[1-3] with parameters^a defined under the table, in comparison with actual computation times using the same parameter setups^b. dFBP and gFFT took ~220 and ~4 times longer than tsFBP according to the theoretical calculation, while these ratios were ~253 and ~7 in the real case. Given the approximate nature of theoretical predictions, the agreement was quite reasonable.

Conclusion

The computational speed of three different radial reconstruction methods was compared theoretically and experimentally. The results show that two-step FBP achieves dramatically enhanced computational efficiency compared to direct 3D FBP, and is also advantageous over 3D FFT with gridding for a large number of channels, while maintaining image quality comparable to both methods. For 3D radial acquisition with many receiver channels, it is expected that two-step FBP could find much use as a rapid image reconstruction method with tolerance to k-space trajectory errors.

Acknowledgements

References

[1] Haccke EM et al., Magnetic Resonance Imaging, 1996.

[2] Block KT et al., In Proceedings of the 19th Annual Meeting of ISMRM, 2011.

[3] Lauterbur PC et al., IEEE Trans Nucl Sci, 1980;27:1227-1231.

[4] Lee JT et al., In Proceedings of the 24th Annual Meeting of ISMRM, 2016.

[5] Park JY et al., Magn Reson Med, 2012;67:428-436.

[6] Bernstein MA et al., Handbook of MRI Pulse Sequences, 2004.