4000
a-f SPARSE: Radial Extension to k-t SPARSE1Electrical Engineering, Case Western Reserve University, Cleveland, OH, United States, 2Biomedical Engineering, Case Western Reserve University, Cleveland, OH, 3Radiology, University Hospitals, Cleveland, OH
Synopsis
a-f SPARSE is a new technique which enables the k-t SPARSE approach to be used for radial trajectories in the Radon domain. Its use for cardiac imaging retrospectively accelerated by a factor of 4 is presented.
Purpose
k-t SPARSE1 is a compressed sensing technique that uses spatiotemporal correlations to enable accelerated imaging. In its original implementation, k-t SPARSE employed the wavelet transform to sparsify dynamic images in the spatial domain, and the Fourier transform in the temporal domain. Compresses sensing has been extended to dynamic radial data through the GRASP2 reconstruction which uses a temporal TV transform sparsity on the image series. Because this is an iterative reconstruction the data must be transformed back-and-forth from the radial k-space to the image domain in each iteration. This step of gridding and degridding the data is time consuming and could induce errors in the final reconstruction. Previous work has demonstrated that it may be possible to take advantage of the symmetry of radial data to accomplish k-t type reconstructions in the a-f space, which would eliminate the need for time-consuming gridding and degridding steps.3 In this abstract we present an extension of Cartesian k-t SPARSE to dynamic radial imaging by using the radial version of the x-f space, the a-f domain, as the sparsity transform.Methods
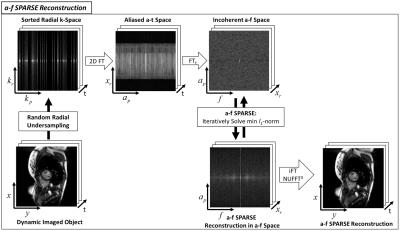
By using the transform concept presented in a-f BLAST, as seen in Figure 1, the Radon transform of the randomly collected radial data can be generated by performing a Fourier transform only along the read-out direction. A subsequent Fourier transform performed along the projection direction leads to an “aliased space”. In this a-t domain the transformed radial data contains aliasing artifacts similar to those that appear in randomly undersampled Cartesian data. As in k-t SPARSE, a Fourier transform can then be applied along the temporal direction, resulting in a representation of the data in a-f space. Due to the random radial sampling pattern this a-f space is sparse, with the type of incoherent aliasing artifacts that can be removed using a compressed sensing reconstruction. As in k-t SPARSE, a-f SPARSE uses iterative soft-thresholding to solve $$$\widehat{\bf{d}}=argmin_d\left\{\parallel{\bf{F}_{2D} \bf{d}-\bf{m}}\parallel_2^2+\lambda\parallel{\bf{F}_t\bf{d}}\parallel_1\right\}$$$ where $$$\bf{m}$$$ is the collected dynamic data in the radial k-space, $$$\bf{d}$$$ is the a-t series to be reconstructed, $$$\bf{F}_{2D}$$$ is the 2D spatial Fourier transform, $$$\bf{F}_{t}$$$ is the temporal Fourier transform, $$$\lambda$$$ is the weighting parameter, and $$$\widehat{\bf{d}}$$$ is the reconstructed a-t series. This formulation is similar to that employed in k-t SPARSE-SENSE4 (although without the use of coil sensitivity information) where the l1-norm enforces the sparsity in the temporal Fourier domain and the l2 -norm enforces the data consistency to a chosen error. Once the SPARSE compressed sensing reconstruction is complete the reconstructed data are transformed back into radial k-space, and then gridded using the NUFFT5, Figure 2.
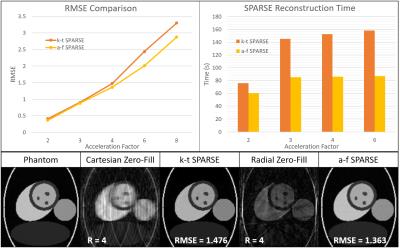
This technique was applied to a cardiac phantom with a heartrate of 60 bpm, matrix size 144x144, and 100 time frames. The data were sampled along both a Cartesian trajectory and a radial trajectory and undersampled to acceleration factors of R=2, 3, 4, 6, and 8. Both k-t and a-f SPARSE reconstructions were applied to the accelerated data (Cartesian and radial, respectively) in order to compare the RMSE values and computation time. No coil sensitivity information was used for the reconstructions. Additionally, a-f SPARSE was tested on retrospectively sampled in-vivo radial cardiac datasets. a-f SPARSE was applied to in-vivo cardiac breathheld cine scans which were downsampled to mimic different acceleration factors. RMSE values were calculated using the fully-sampled cine images. These data were collected along a radial trajectory on a Siemens Skyra 3T whole-body scanner with a bSSFP sequence using TR = 29 ms, TE = 1.5ms, BW = 1 kHz, FoV = 300mm, spatial resolution = 2.3x2.3x8.0 mm3, flip-angle = 57 degrees.
Results
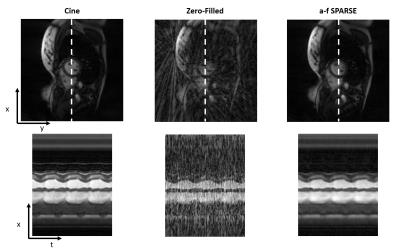
The RMSE and computation time comparisons between a-f SPARSE and k-t SPARSE in Figure 3 show a-f SPARSE outperforming k-t SPARSE for all acceleration factors. Figure 4 shows that for reconstruction of R=4 a-f SPARSE preserves the temporal resolution in the x-t image while reducing the radial artifacts from the retrospectively undersampled cine dataset. Figure 5 is a gif of the same dataset in Figure 4 showing the result of applying a-f SPARSE to the dynamic dataset.Discussion/Conclusion
a-f SPARSE enables rapid reconstruction of radially undersampled images by removing the gridding/degridding steps from an iterative compressed sensing reconstruction. The a-f SPARSE reconstruction demonstrates that the a-f space can be used in compressed sensing reconstructions to speed up the reconstruction of dynamic radial data.Acknowledgements
Our lab receives research support from Siemens Healthcare.References
1. Lustig, M., Santos, J. M., Donoho, D. & Pauly, J. M. k-t SPARSE: high frame rate dynamic MRI exploiting spatio-temporal sparsity. Proc. ISMRM, Seattle 50, 2420 (2006).
2. Feng, L. et al. Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn. Reson. Med. 717, 707–717 (2013).
3. Kretzler, M., Hamilton, J., Griswold, M. & Seiberlich, N. a-f BLAST: A Non-Iterative Radial k-t BLAST Reconstruction in Radon Space. in ISMRM (2016).
4. Otazo, R., Kim, D., Axel, L. & Sodickson, D. K. Combination of Compressed Sensing and Parallel Imaging for Highly Accelerated First-Pass Cardiac Perfusion MRI. Magn. Reson. Med. 29, 997–1003 (2010).
5. Fessler, J. A. & Sutton, B. P. Nonuniform fast fourier transforms using min-max interpolation. IEEE Trans. Signal Process. 51, 560–574 (2003).
Figures