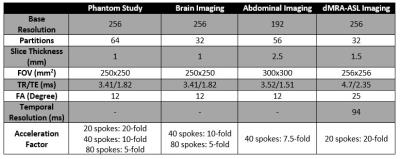
3999

Golden-Ratio Rotated Stack-of-Stars Acquisition for Improved Volumetric MRI

Ziwu Zhou¹, Fei Han¹, Lirong Yan², Danny J.J. Wang², and Peng Hu¹

¹Radiological Sciences, University of California, Los Angeles, Los Angeles, CA, United States, ²Neurology, University of Southern California, Los Angeles, CA, United States

Synopsis

In this abstract, we developed and evaluated an improved stack-of-stars (SOS) sampling strategy that can efficiently sample 3D k-space and reduce streaking artifacts. Compared with conventional SOS sampling strategies that collect the same radial angle for every slice, proposed method rotates the spokes in a golden-angle manner along the slice direction, which modifies the aliasing pattern resulted from k-space under-sampling. With either gridding reconstruction or more advanced methods, proposed rotated SOS sampling strategy provides improved image quality with reduced streaking artifacts and better delineation of fine structures.

Introduction

Stack-of-stars (SOS) sampling is a widely used 3D k-space trajectory for fast MRI. In conventional 3D SOS acquisition strategies^1-3, the azimuthal angles of the radial spokes do not vary in the slice direction. Several previously proposed methods^4-6 vary the angle of the radial spokes or spiral interleaves in a linear fashion in the slice direction; however, we show in this report that such a strategy is sub-optimal. We propose a rotated SOS (RSOS) sampling method in which radial spokes are rotated in a golden-ratio⁷ fashion in the slice encoding direction, i.e. RSOS-GR. We show that our RSOS-GR strategy creates varying aliasing patterns along the slice direction, and such a varying aliasing pattern improves the condition of the inverse problem in a parallel imaging reconstruction and improves the incoherence of the sampling function in a compressed sensing reconstruction.

Methods

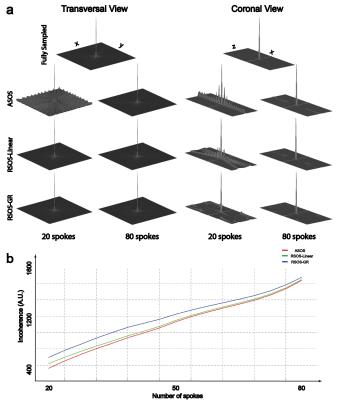
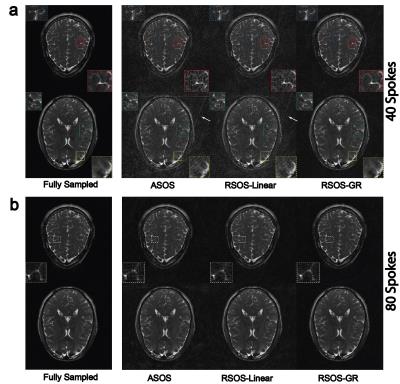
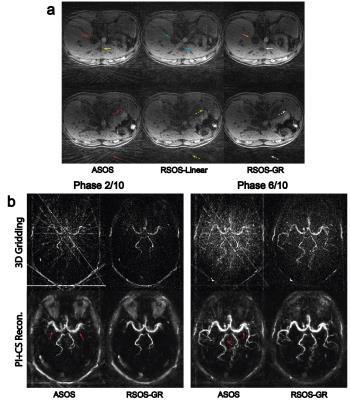
Rotating Stack-of-Stars: In conventional aligned SOS (ASOS), angle $$$\theta_i$$$ of the $$$i^{th}$$$ spoke out of total $$$N_r$$$ spokes in each slice is calculated as: $$$\theta_i=\frac{\pi}{N_r}*(i-1)$$$, $$$i=1,2,...,N_r$$$. In the proposed RSOS-GR, non-zero azimuthal angle offsets that change across the slices are introduced as follows: $$$\varphi_G(j)=mod((j-1)*\frac{\pi}{N_r}*\frac{\sqrt{5}-1}{2},\frac{\pi}{N_r})$$$, $$$j=1,2,...,N_{PE}$$$, where $$$N_{PE}$$$ is the total number of slices and $$$j$$$ is the slice index. Subsequently, the angle for the $$$i^{th}$$$ radial spoke in the $$$j^{th}$$$ slice is calculated as $$$\theta_i+\varphi_G(j)$$$. As a comparison, the effect of using linear (RSOS-Linear) angle offset function $$$\varphi_L(j)=\frac{j-1}{N_{PE}}*\frac{\pi}{N_r}$$$, $$$j=1,2,...,N_{PE}$$$ was also studied in this work. Computer Simulation: The point spread functions (PSF) of the three strategies were first compared using simulations. The PSF was calculated by first setting each sampled point in k-space trajectories to unit value. Resultant k-space data were then gridded onto Cartesian grid using 3D gridding⁸. Finally, the PSF was obtained as the inverse Fourier transform of the gridded Cartesian k-space. To quantitatively assess the PSFs, the ratio of the main lobe magnitude to the standard deviation of the side-lobes magnitude was calculated as a measure of the incoherence of the 3D PSF⁹. Phantom Experiment: To evaluate the performance of the three strategies, a phantom experiment was performed on a 3.0T MRI scanner (Siemens Prisma). A fully-sampled reference data (400 spokes per slice, ASOS) and nine additional prospectively under-sampled data sets (20 spokes, 40 spokes, and 80 spokes per slice, ASOS, RSOS-Linear and RSOS-GR) were acquired. In-vivo Experiment: The three strategies were then tested in three different applications: brain imaging, abdominal imaging, and dynamic MRA (dMRA) using arterial spin labeling (ASL)¹⁰. All experiment were performed on the same 3.0T scanner. Brain and abdominal imaging were performed on one healthy volunteer in axial orientation. A fully sampled data and six prospectively under-sampled data sets (40 spokes and 80 spokes per slice, ASOS, RSOS-Linear and RSOS-GR) were acquired for brain imaging, while for abdominal imaging three data sets with 40 spokes per slice using the three strategies were acquired with a total scan time of 18s each during breath-holds. DMRA-ASL imaging was performed on another volunteer, with only two data sets were acquired using ASOS and RSOS-GR with 20 spokes per slice per temporal phase, with a total of 10 phases. All imaging parameters were listed in Table 1. For the phantom, brain and abdominal imaging experiments, acquired data sets were reconstructed with 3D gridding. To demonstrate the efficacy of RSOS in advanced image reconstruction methods, acquired data sets in the dMRA-ASL imaging experiment were reconstructed with 3D gridding and a parallel imaging-compressed sensing (PI-CS) combined reconstruction method¹¹.

Results

Figure 1 shows the simulated PSFs and the quantitative incoherence comparison of the three strategies. As shown, the proposed RSOS-GR method has greatly reduced side-lobes and higher incoherence compared with the other two strategies. Figure 2 shows two representative slices of phantom images. At high under-sampling factor, severe streaking artifacts were seen on ASOS and RSOS-Linear, while proposed method had much reduced artifacts. Figure 3 shows the representative brain images. Similar to phantom experiment, streaking and blurring were greater when using ASOS or RSOS-Linear, especially at higher under-sampling factors; in comparison, images acquired with RSOS-GR had reduced artifacts and improved delineation of small features. Figure 4a,b shows the abdominal and dMRA-ASL images, respectively. Again, the RSOS-GR approach provided better reconstruction quality compared with the other two strategies, with either simple gridding or more advanced PI-CS algorithm.

Conclusion

We have presented a golden ratio rotated SOS sampling strategy that provides improved image quality compared with conventional aligned strategy or SOS with a linear angle rotation.

Acknowledgements

Research reported in this abstract was supported by National Institutes of Health under award numbers R01HL127153, R01EB014922, 16SDG29630013.

References

1. Peters DC, Korosec FR, Grist TM, Block WF, Holden JE, Vigen KK,Mistretta CA. Undersampled projection reconstruction applied to MR angiography. Magn Reson Med 2000;43:91–101.

2. Cashen TA, Jeong H, Shah MK, Bhatt HM, Shin W, Carr JC, Walker MT, Batjer HH, Carroll TJ. 4D radial contrast-enhanced MR angiography with sliding subtraction. Magn Reson Med. 2007; 58: 962–972.

3. Feng L, Grimm R, Tobias Block K, Chandarana H, Kim S, Xu J, AxelL, Sodickson DK, Otazo R. Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med 2014;72:707–717.

4. Chen L, Adluru G, Schabel MC, McGann CJ, Dibella EV. Myocardial perfusion MRI with an undersampled 3D stack-of-stars sequence. Med Phys 2012;39:5204–5211.

5. Breuer FA, Bauer S, Blaimer M. Self-Calibrating Stack-of-Stars (SoS)-CAIPIRINHA for Improved Parallel Imaging. In Proceedings of the21st Annual Meeting of ISMRM, Salt Lake City, Utah, USA, 2013.p. 3824.

6. Deng W, Zahneisen B, Stenger VA. Rotated stack-of-spirals partial acquisition for rapid volumetric parallel MRI. Magn Reson Med 2016;76:127–135.

7. Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the golden ratio for time-resolved MRI. IEEE Trans Med Imaging 2007;26:68–76.

8. Beatty PJ, Nishimura DG, Pauly JM. Rapid gridding reconstruction with a minimal oversampling ratio. IEEE Trans. Medical Imaging. 2005;vol. 24(no 6):799–808.

9. Lustig M, Donoho D, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182–1195.

10. Song HK, Yan L, Smith RX, Xue Y, Rapacchi S, Srinivasan S, Ennis DB,Hu P, Pouratian N, Wang DJJ. Noncontrast enhanced four-dimensional dynamic MRA with golden angle radial acquisition and K-space weighted image contrast (KWIC) reconstruction. Magn Reson Med. 2014;72:1541–1551.

11. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71:990–1001.

Figures

Table 1. Imaging parameters in different applications.

Figure 1. (a) The PSF of fully-sampled and ASOS, RSOS-Linear and RSOS-GR k-space sampling with 20 spokes and 80 spokes per slice in transversal and coronal views. ASOS produces strong streaking artifact at high acceleration factor (20 spokes). With 80 spokes, there are no significant difference between the three sampling strategies; with 20 spokes, RSOS-GR has reduce energy in the PSF sidelobes compared with ASOS and RSOS-Linear in the coronal view. (b) Calculated incoherence based on the 3D PSFs with different number of spokes per slice. RSOS-GR has superior PSF incoherence compared with ASOS and RSOS-Linear.

Figure 2. Phantom images acquired with different sampling strategies and with 20, 40 and 80 spokes per slice. From left to right, each column in Fig (a), (b) and (c) shows two representative axial slices from the 3D images acquired with: fully-sampled, ASOS, GSOS-Linear, and RSOS-GR, respectively. Fig (a), (b) and (c) show three under-sampling scenarios: 20 spokes, 40 spokes and 80 spokes per slice, respectively.

Figure 3. Selected brain images acquired with different sampling strategies and number of spokes per slice. Similar to Figure 2, each column in Fig (a) and (b) shows two representative axial slices from the 3D images acquired with: fully-sampled, ASOS, GSOS-Linear, and RSOS-GR, respectively. Fig (a) and (b) show two under-sampling scenarios: 40 spokes and 80 spokes per slice, respectively.

Figure 4. (a) Two representative slices of abdominal images. RSOS-GR provides images with less streaking artifacts and sharper structures. (b) MIP images at two phases of dMRA-ASL images acquired with ASOS and RSOS-GR. Even with only 20 spokes per slice per phase, RSOS-GR is still able to reduce majority of streaking artifacts compared with ASOS using 3D gridding reconstruction. With a PI-CS reconstruction, overall image quality was improved for both acquisitions. However, blurring of vessels and residual streaking artifacts can still be seen on images with ASOS acquisition while RSOS-GR acquisition provides cleaner and sharper images.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

3999