Purpose

T1 estimation based upon multiple flip angles(MFA) is widely used clinically due to shorter data acquisition time¹. Accuracy of T1 map depends upon appropriate numbers of flip angle(FA). Currently, there is no accepted FA set, that is used to minimize the uncertainty over T1 estimation² . However, MFA is preferred when imaging over large T1 range³ as at low or high T1 values dual FA reduces the efficiency¹ due to high noise bias. Moreover, errors in T1 estimation propagates to kinetic parameter estimation⁴. The objective of this study was to propose a Neural Network(NN) based supervised machine learning approach that predict additional FA data using limited available FAs data, thereby producing improved T1 estimation in reduced scan time.

Method

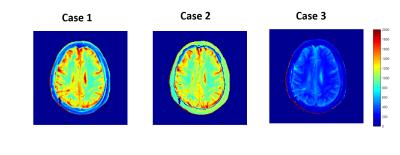
This study was done for experimental as well as simulation data on FA set[3⁰,6⁰,10⁰,15⁰], used routinely for clinical purpose in a local hospital. MRI study was conducted on brain of 15 tumor patients at 3T(Ingenia,PhilipsHealthcare) scanner with TR=6ms. T1 estimation was done using a non-linear least-square fitting of the pixel-wise image intensities at MFAs to the theoretical equation for SPGR signal intensity⁴. B1-inhomogeneity correction was done using saturated double-angle method⁵. Different Case studies were done. In Case-1, all four FA[3⁰,6⁰,10⁰,15⁰] were used to compute T1 map. In Case-2, a NN was used to predict data for FA-3⁰ from FA[6⁰,10⁰,15⁰] and T1 map was computed using acquired FA[6⁰,10⁰,15⁰] data and predicted FA-3⁰ . The NN parameters were optimized to 1 hidden layer with 3 nodes by iteratively training. In Case-3, T1 map was computed using three FA[6⁰,10⁰,15⁰] data. In Case-4, we used a NN, with 1 hidden layer having 4 nodes, to predict FA data at [3⁰,10⁰] from data at [6⁰,15⁰]. In this case, T1 map was computed using acquired FA[6⁰,15⁰] data and predicted FA[3⁰,10⁰] data. In Case-5, T1 was computed using only two FA[6⁰,15⁰] data. Relative percentage error(RPE) in T1 computation was calculated at each voxel for all Cases with respect to Case-1. NN was trained and optimized using data of 10 patients and the efficacy of the model was tested on remaining 5 patients. In simulated data T1 values[800,1200,1800,2400 ms] corresponding to 4 tissues in a tumor brain(GM,WM,Tumor,CSF) was used. Noise upto 30 % was incorporated in the data. A NN, was trained on 15000 data points for each T1 value. The efficiency of the NN model was tested at different noise levels, to mimic real data.

Results

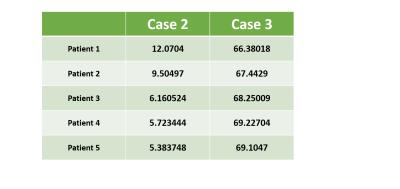
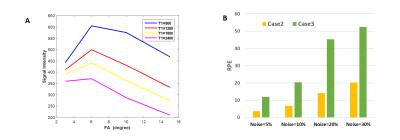
Fig-1 results show that T1 map obtained in Case-2 is similar to that of Case-1 whereas T1 map obtained in Case-3 is a significantly underestimated. Table-1 shows that Case 2 has a nominal RPE(~5-12 %) compared to a high RPE in Case 3 (~66-70 %) for 5 patients. Fig-2(A) shows the simulated signal intensity curves corresponding to 4 different T1 values. Fig-2(B) shows Case-3, has much higher RPE compared to Case-2, at different noise levels. Fig-3(A) shows that in experimental data the RPE in Case-5 is higher than Case-4, for all 5 patients except 1. Fig-3(B) shows that in simulated data, the difference in RPE of estimated T1 map is comparatively much less in Case-4 compared to Case-5. Simulation result, also shows, that RPE is proportional to noise in data.

Discussion

The results show that the proposed method for T1 estimation produces significantly better accuracy(Case-2 and Case-4) compared to their counterparts(Case-3 and Case-5) in both experimental and simulation data. In real life scenario, where data for one of the FA data can get corrupted due to motion or other artifacts, proposed approach can recover this data. Accuracy can depend on the importance of FA that is being predicted. It was found that T1 maps estimated using FA[3⁰,6⁰,10⁰] produces similar accuracy as that obtained using, known FA[3⁰,6⁰,10⁰] data and predicted FA-15⁰data, thus highlighting the relatively less importance of FA-15⁰ in fitting data to the standard equation. A careful trade-off has to be done before choosing which FA data should be predicted. The accuracy of NN model can be further increased by training it with a larger number of patients so that data with noise can be modelled. Since the NN tries to predict data governed by standard equation, it remains to be seen if modelling NN with a known relation between input and output, produces better accuracy or not.

Conclusion

The results shows the advantage of using a machine learning approach to predict additional FA data which can be used to estimate T1 map. This method reduces scan time as well as increases the accuracy of T1 estimation compared to lesser FA dataset.

Acknowledgements

The authors acknowledge internal grant from IIT-Delhi and technical support of Philips India Limited in MRI data acquisition. We thank Dr. Indrajit Saha for providing technical support for MRI data acquisition; Dr Pradeep Gupta in data acquisition.