Synopsis

An online learning algorithm is used to derive a generic model for dynamic cardiac MR data from a large set of training data. Image quality of reconstructed data could be improved and smoothing in time domain reduced.

Introduction

Image reconstruction employing data specific transforms allows for enhanced transform domain sparsity and hence higher undersampling factors than generic transforms like Wavelet or Fourier transforms. Challenging remains to find the data specific transform from the undersampled data. For dynamic data sets, principal component analysis is commonly used to derive a transform domain from a fully sampled, low-resolution training data set^1,2. Further improvements were reported by updating the transform during reconstruction³. More recent algorithms use overcomplete dictionaries or nonlinear algorithms to capture more image details⁴.

In this work, a model for dynamic cardiac MR image data is learned from a large training data set comprising of several hundred high-resolution scans. Image reconstruction is performed using sparse reconstruction and compared to k-t Sparse and model reconstruction based on randomly selected small subsets.

Methods

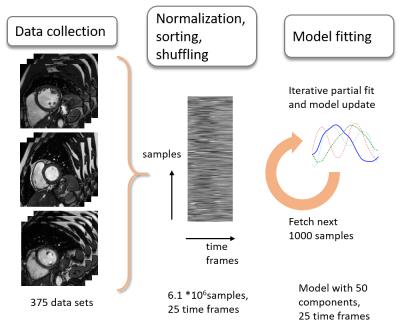
Dynamic cardiac MRI data sets were acquired in 186 subjects on 1.5 and 3T systems (Philips Healthcare, Best, The Netherlands) with acquitision matrix sizes from 192x192 to 288x288 and 25 dynamics. A total number of 375 dynamic 2D short-axis scans were used as input for the model generation. Each dynamic image series was normalized by subtracting the median image value along time and dividing each frame by its standard deviation. The data was cropped to 128x128 data points per frame. Time profiles of all data sets were combined in a matrix and shuffled. To learn a model from this large training data matrix, an online dictionary learning⁵ algorithm was employed. Each step of the algorithm, a batch of 1000 samples was processed in a partial model fit with equal weight (Figure 1). The partial fit was calculated by solving the dictionary learning minimization problem:

$$\mathrm{argmin}_{U,V} = 0.5 || Y - U V||_2^2 + \alpha ||U||_1 \;\;\;\mathrm{with}\; ||V_k||_2 = 1 \;\; \mathrm{for}\;\mathrm{all}\;\; 0 <= k <= n_{\mathrm{components}}$$

where Y are the training data for a single step, V is the learned dictionary, and U the training data in the sparse domain.

Test data were acquired in three subjects on a 3T systems with a 28-channel coil array. Scan parameters included a field-of-view of 270x270 mm2, slice thickness: 8 mm, TR/TE: 3.8/1.84 ms, voxel size: 1.4x1.4 mm2, flip angle: 45°, acquisition matrix: 192x192. No image data of the test subjects were included in the training data for the model. All k-space data sets were pre-whitened with the noise covariance matrix and compressed to 10 virtual coils. K-space profiles were retrospectively undersampled along phase-encode direction using a Cartesian pseudo-random undersampling pattern with a reduction factor of 6.5, resulting in 30 profiles per frame. Image reconstruction was performed by minimizing the sparse MRI L₁ optimization problem

$$\mathrm{argmin}_i ||Ei-d||_2^2 + ||φ(i)||_1$$ with φ being the sparsifying transform. The minimization was performed with a Lasso⁶ algorithm. For the proposed method, φ is given by the learned model matrix, mapping the time dimension to components of the model space. Image reconstruction results were compared to k-t Sparse with a Fourier Transform along time as sparsifying transform and transforms based on reduced models learned from subsets of ten randomly selected training data sets. The reconstruction with a reduced model was repeated six times with different subsets. Model generation and image reconstruction was implemented in Python using SciPy⁷. Computation time of the model was below one hour and reconstruction time of MR image data was on the order of several minutes.

Results

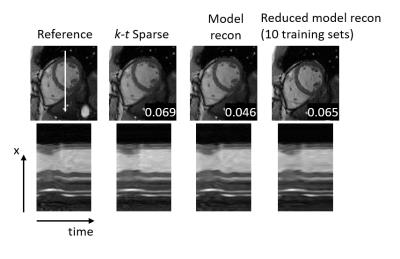
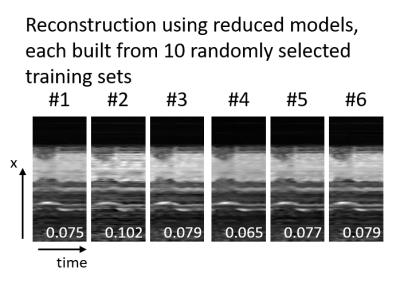
Image reconstruction results are shown in Figure 2. The image data reconstructed with the proposed model generation has a lower RMSE and improved perceived image quality. k-t Sparse reconstruction data shows increased smoothing artifacts in the time domain. Images reconstructed with a reduced model derived from a small training data set could improve image quality only to a lesser extent. Reconstruction results of the reduced model depended largely on the randomly selected subset. Figure 3 shows six results for models from different subsets of the training data, each based on ten randomly selected 2D dynamic cardiac scans.

Conclusion

Machine learning can be used to compute generic models for dynamic cardiac MRI and enhance image reconstruction results. The selection of the training data affects the image quality of the reconstructed data. Online learning algorithms can be used to process large amounts of training data to include more features and improve reconstruction results.

Acknowledgements

References

1. Lustig, Michael, et al. "kt SPARSE: High frame rate dynamic MRI exploiting spatio-temporal sparsity." Proceedings of the 13th Annual Meeting of ISMRM, Seattle. Vol. 2420. 2006.

2. Jung, Hong, et al. "k-t FOCUSS: A general compressed sensing framework for high resolution dynamic MRI." Magnetic Resonance in Medicine 61.1 (2009): 103-116.

3. Lingala SG, Jacob M. Blind compressive sensing dynamic MRI. IEEE Trans. Med. Imaging 2013;32

4. Doneva, Mariya, et al. "Compressed sensing reconstruction for magnetic resonance parameter mapping." Magnetic Resonance in Medicine 64.4 (2010): 1114-1120.

5. Mairal, Julien, et al. "Online dictionary learning for sparse coding." Proceedings of the 26th annual international conference on machine learning. ACM, 2009.

6. Tibshirani, Robert. "Regression shrinkage and selection via the lasso." Journal of the Royal Statistical Society. Series B (Methodological) (1996): 267-288.

7. Jones, Eric, Travis Oliphant, and P. Peterson. "Open source scientific tools for Python." (2001).