3984
Undersampling trajectory design for fast MRI with super-resolution convolutional neural networkShanshan Wang1, Taohui Xiao1,2, Sha Tan1,3, Yuanyuan Liu1, Leslie Ying4, and Dong Liang1
1Paul C. Lauterbur Research Center for Biomedical Imaging, SIAT, Chinese Academy of Sciences, Shenzhen, People's Republic of China, 2School of Physics and Optoelectronics, Xiangtan University, Xiangtan, People's Republic of China, 3School of Information Engineering, Guangdong University of Technology, Guangzhou, People's Republic of China, 4Department of Biomedical Engineering and Department of Electrical Engineering, The State University of New York, NY, United States
Synopsis
Deep learning based fast MR imaging (DeepLearnMRI) has been an appealing new research direction, which utilizes networks to draw valuable prior information from enormous existing high-quality MR images and then assists accurate MR image reconstruction from undersampled data. This paper explores optimal undersampling trajectory for DeepLearnMRI. Specifically, we designed hamming filtered asymmetrical 1D partial Fourier sampling scheme for fast MR imaging with our developed super-resolution convolutional neural network. Experimental results on in vivo dataset show that the proposed scheme allows DeepLearnMRI to reconstruct more accurate MR images with less time compared to the Classical GRAPPA and SPIRiT.
Introduction
Employing deep learning for accelerating MR scan (DeepLearnMRI) has been an appealing new research direction1,2,3, which allows very quick MR image reconstruction from highly undersampled Fourier data. Specifically, different from the popular compressed sensing/parallel imaging techniques, which explore sparsity/sensitivity for fast MRI, DeepLearnMRI learns the end-to-end mapping between zero-filled and fully sampled MR image from enormous offline acquisitions and then aids accurate online fast MR imaging with this valuable mapping prior. Therefore, conventional sampling trajectories, such as incoherently and uniformly undersampling, which are required for compressed sensing and parallel MRI respectively4, may not be the optimal undersampling trajectory for DeepLearnMRI. This work designs Hamming filtered asymmetrical 1D partial Fourier sampling scheme for fast MR imaging with our developed super-resolution convolutional neural network (SuperCNN) 5. The scheme allows deep learning to have its own specific settings for fast MR imaging.Theory and method
yThe proposed scheme is to reduce the number of phase encodings required for DeepLearnMRI. To realize this, its design mainly consists of two parts 1D partial Fouier and Hamming filter. Let $$$u$$$ denote the MR image, $$$E$$$ represent the Fourier transform or multi-coil encoding function, $$$M$$$ stand for 1D partial Fourier mask, and $$$H$$$ means the Hamming filter, then the undersampled K-space data can be described as $$$y=HMEu$$$. For offline training, the undersampling mask consists of a number of symmetrically and asymmetrically sampled masks filtered by the Hamming windows $$$H$$$, whose examples can be seen in Fig. 1. The whole off-line training framework is also provided in Fig. 2 with one training pair shown. The inputs consist of low-resolution MR images with diverse level of fine structures information since different undersampling masks cover different k-space regions. The image reconstructed from the full data are used as labels for the SuperCNN training. Then the trained SuperCNN is used to predict an online image from the low-resolution image obtained from one zero-filled undersampled data with a Hamming filtered asymmetrical 1D partial Fourier sampling trajectory. For the online MR image testing, it should be noted that only one undersampling mask is used for undersampling, which is asymmetrical and always covers the K-space center.Experiment
The training data consists of over 4000 fully sampled MR brain slices we collected from a 3T scanner (SIEMENS MAGNETOM Trio). Informed consent was obtained from the imaging subject in compliance with the Institutional Review Board policy. Undersampled measurements were retrospectively generated using a number of the proposed undersampling schemes shifted from the k-space center. To increase the robustness of the proposed approach, overlapping image patches were extracted from the images to increase training datasets, among which 90% are used for updating the network dataset and the rest 10% for validating the training process. We use three layers of convolution for the network with the following configurations (64 nodes for the 1st layer with a kernel size 9*9, 32 nodes for the 2nd layer with a kernel size of 5*5, 1 node with size of 5*5). The SuperCNN offline training took almost four days on a workstation equipped with 128G memory and a processor of 16 cores (Intel Xeon (R) CPU E5-2680 V3 @2.5GHz). Then the trained network with the proposed Hamming filtered asymmetrical 1D partial Fourier sampling trajectory was evaluated on in-vivo transversal brain datasets, which were acquired on a 3T scanner (SIEMENS MAGNETOM Trio) with a 12-channel head coil by T1-weighted turbo spin-echo (TSE) sequence (TE=11.0ms, TR=928ms, FOV=18×18 cm, matrix=256×256, slice thickness=2mm). The proposed method was additionaly evaluted with the 1D uniform undersampling as GRAPPA and SPIRiT, and also 1D random undersampling mask with variable density.Result and discussion
Fig. 2 presents the reconstruction results of the comparison methods and the proposed method with different undersampling schemes. It can be observed that the results produced by SPIRiT and GRAPPA still consist of noise and visible artifacts, while SuperCNN could produce a better image closer to the ground truth. Nevertheless, with different masks, the proposed method predicts different reconstruction results. For a closer comparison, the white box enclosed areas are also enlarged, which show the proposed scheme allows the proposed method to produce a better image compared to the other two undersampling schemes. Furthermore, although the off-line training takes roughly four days, the online test for the proposed method is 14.9 seconds on a regular computer on a Windows 10 (64-bit) operating system equipped with 8GB RAM and Intel(R) Core(TM) i3 -3240 CPU @3.40GHz.AMD 3.40GHz in MATLAB 2014b. While GRAPPA and SPIRiT respectively need 46.7 and 34.7 seconds, which are respectively over 3 or 2 times of our computational time.Acknowledgements
Grant support: China NSFC 61471350, 61601450, the Natural Science Foundation of Guangdong 2015A020214019, 2015A030310314, the Basic Research Program of Shenzhen JCYJ20140610152828678, JCYJ20160531183834938, JCYJ20140610151856736 and the youth innovation project of SIAT under 201403 and US NIH R21EB020861 for Ying.References
1.Shan W , Zhenghang S, Xi P and Dong L.Exploiting deep convolution neural network for fast resonance imaging. ISMRM, 2016; 1778. 2.Kwon K, Kim D, Seo H, Cho J, Kim B and Park H. Learning-based reconstruction using artificial neural network for higher acceleration. ISMRM, 2016; 1801 3. Golkov V, Dosovitskiy A, Sperl J.I, M. Czisch, et al. q-Space Deep Learning: twelve-fold shorter and model-free diffusion MRI scans," IEEE TMI. 2016; 35(5): 1344-1351. 4. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. MRM, 2007; 58(6):1182-95. 5. Shan W, Zhenghang S, Leslie Y, Xi P, Shun Z, et al. Accelerating magnetic resonance imaging via deep learning. IEEE ISBI, 2016; 514-517.Figures
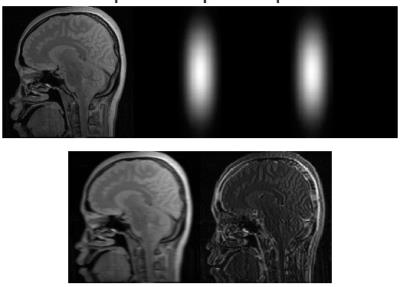
Figure 1: From left to right and top to bottom: Ground-truth MR image, Hamming filtered symmetrical
1D partial Fourier sampling trajectory example, Hamming filtered asymmetrical
1D partial Fourier sampling trajectory example and their corresponding undersampled images
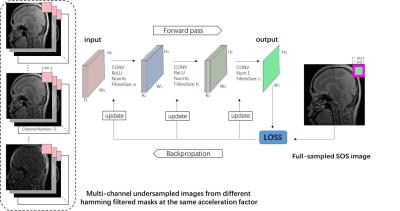
Figure 2: The
offline training framework with diverse proposed masks: A training pair of
input and output example
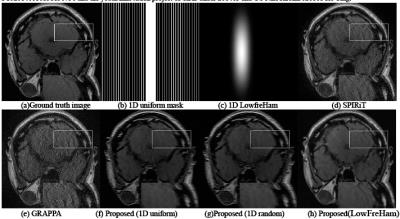
Figure 3: From left to right and top to bottom: (a)
Ground-truth MR image; (b) 1D uniform undersampling mask with ACS lines; (c)
Hamming filtered asymmetrical 1D partial Fourier sampling trajectory; The
reconstructions of the SPIRiT (d) and GRAPPA (e) with 1D uniform undersampling
mask. The reconstruction results of the proposed method with uninform
undersampling (f), 1D random undersampling (g) and the proposed undersampling
scheme (h) from 25% of sampled data.