3974
Cascaded Convolutional Neural Network (CNN) for Reconstruction of Undersampled Magnetic Resonance (MR) Images1Yonsei University, Seoul, Korea, Republic of
Synopsis
We propose cascaded CNN operating on k-space and image domain alternatively for reconstruction of undersampled MR images. Our cascaded CNN is capable of restoring most of detailed structures in the full-sampled image while sufficiently removing undersampling artifacts.
Introduction
Acceleration of magnetic resonance (MR) imaging is one of the most important issue in the field of MR image reconstruction. Compressed sensing (CS)-based methods which use sparsity in specific transform domains such as wavelet and image-adaptive domains [1, 2] were used to recover undersampled images. However, these techniques had limits in recovering one single-contrast undersampled MR image because it could not sufficiently remove artifacts and blurred images. Recently, deep-learning-based reconstruction methods [3, 4] have been introduced and showed better performance compared with conventional CS-based optimization methods. However, they also had limits in recovering some detailed structures that disappear in undersampled images because they are performed for those images that already lose the detailed structures. To recover the disappeared structures due to undersampling, we developed an interpolation methods for k-space itself based on deep convolutional neural network (CNN). Then, another deep CNN that sharpens and removes artifacts in image domain was applied. For data consistency, sampled k-space data were re-filled into k-space of each network output. Consequently, we propose a cascaded CNN that consists of two CNNs operating on k-space and image domain.
Methods
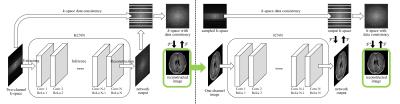
Our proposed cascaded CNN consists of three parts; deep CNN for interpolating k-space (KCNN), deep CNN for image sharpening and artifacts removal (ICNN), and data consistency. The network architecture are presented in Fig. 1. Our first network, KCNN, interpolates non-sampled points of undersampled k-space data using adjacent sampled k-space points. First, all k-space data of training images are retrospectively undersampled with the same undersampling pattern. Then, to train CNN that learns inherent relationship between undersampled k-space and fully-sampled k-space, the two data are fed as inputs and outputs of KCNN. KCNN consists of three parts; extracting part, inference part, and reconstruction part. In extracting part, features of input which is two-channeled k-space data (real and imaginary) are extracted by one convolution/rectified linear unit (ReLU) layer and concatenated. Inference part results in same-size and same-number outputs while passing through multiple convolution/ReLU layers. Final two-channeled k-space is reconstructed through reconstruction part which takes weighted combination of outputs of previous layer. To sharpen detailed structures and remove remaining artifacts in the image reconstructed from KCNN, we developed another network using deep CNN (ICNN) which operates in image domain. ICNN basically consists of the same networks with KCNN except for the number of channels. We regenerated new training data (one-thousand k-space data) by feeding the original training data to well-trained KCNN and refilling sampled k-space points to the network outputs. The new training data was inverse-Fourier-transformed and fed to ICNN for network inputs. For data consistency, sampled k-space data were also refilled to the k-space of the network outputs (output images) which resulted in ICNN. All this process is one block of our cascaded CNN. This block was repeated until the loss between the fully-sampled image and the final output is saturated.
Experiments
We obtained 1000 T2 fluid attenuated inversion recovery brain images (field strength = 3.0 T, slice thickness = 5.0 mm, TE = 90 ms, TR = 9000 ms, size = 256×256) from Alzheimer's Disease Neuroimaging Initiative MRI data [5]. Among 1000 images, 995 images were used for training and the others were used for test. Undersampled data were acquired retrospectively using 2D Poisson disk sampling mask with acceleration factor 6 and 2D variable density Cartesian sampling mask with acceleration factor 3. Detailed parameter information for the proposed method is as follows: patch size = 41×41, N (number of layers) = 24, kn (convolution filter size) = 3×3 and mn (number of convolution filter) = 64, repetition number of blocks = 2. Training required approximately one day to be completed using Caffe library [6] with an Intel 3.40 GHz CPU, GeForce GTX TITAN, and 64 G memory.Results
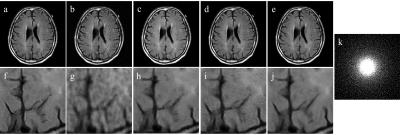
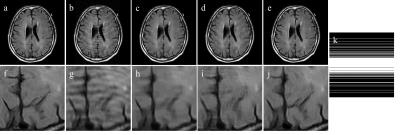
Fig. 2 and Fig. 3 shows the reconstruction results of Poisson undersampling (R = 6) and Cartesian undersampling (R = 3), respectively. True image (a), zero-padded image (b), CS image (c), image reconstructed with CNN in only image domain (d), image reconstructed with our cascaded CNN (e), their magnified images (f-j), and undersampling pattern (k) are shown. (h) shows fewer undersampling artifacts than (g, h), however, it failed to restore disappeared detailed structures due to undersampling. (j) preserved most of detailed structures in (f), demonstrating our cascaded CNN could effectively restore and sharpen detailed structures with less artifacts.Conclusions
We propose cascaded CNN operating on k-space and image domain alternatively for reconstruction of undersampled MR images. Our method could restore most of detailed structures in the full-sampled image while sufficiently removing undersampling artifacts.Acknowledgements
This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No. 2016R1A2B4015016).References
[1] Lustig, Michael, David Donoho, and John M. Pauly. "Sparse MRI: The application of compressed sensing for rapid MR imaging." Magnetic resonance in medicine 58.6 (2007): 1182-1195.
[2] Ravishankar, Saiprasad, and Yoram Bresler. "MR image reconstruction from highly undersampled k-space data by dictionary learning." IEEE transactions on medical imaging 30.5 (2011): 1028-1041.
[3] Sinha, Neelam, A. G. Ramakrishnan, and Manojkumar Saranathan. "Composite MR image reconstruction and unaliasing for general trajectories using neural networks." Magnetic resonance imaging 28.10 (2010): 1468-1484.
[4] Wang, Shanshan, et al. "Accelerating magnetic resonance imaging via deep learning." Biomedical Imaging (ISBI), 2016 IEEE 13th International Symposium on. IEEE, 2016.
[5] ADNI data, ‘Alzheimer’s Disease Neuroimaging Initiative’ http://adni.loni.usc.edu/, accessed April, 2016
[6] Jia, Yangqing, et al. "Caffe: Convolutional architecture for fast feature embedding." Proceedings of the 22nd ACM international conference on Multimedia. ACM, 2014.
Figures