3970

Field-of-View Packing and k-Space Fast Sampling

Yudong Zhu¹

¹Zhu Consulting, Scarsdale, NY, United States

Synopsis

By natural or artificial arrangement, excited spins may cluster in discrete areas of a multi-dimensional image-space. By leveraging gaps in-between, one may under-sample k-space while preserving the ability to map the spin distribution. FOV-packing is a new technology that maximizes efficiency mapping gapped distribution (spatially, spectrally and etc.) and extends reach. When applied to simultaneous multi-slice MRI, it leads to a unique technique that is speedy (due to sampling of image space and acceleration of encoding), with √N SNR scaling (due to volumetric encoding’s noise averaging effect) and super-resolution capability (due to FOV packing and the option of resolving sub-slices).

Introduction

Central to imaging speed, resolution and field-of-view (FOV), k-space sampling and Nyquest rate are among the core concepts of MRI. By natural or artificial arrangement, signal-contributing (excited) spins may cluster in discrete areas of a multi-dimensional image-space. By leveraging gaps in-between, one may under-sample k-space while preserving the ability to map the spin distribution. This has significant implication for imaging performance. We propose an imaging technique that, based on “FOV-packing”, quickly probes or samples an extensive image-space with coarse k-space sampling. A rather visual and important example is the technique’s treatment of simultaneous multi-slice imaging (SMS)¹ as a spatially-sampled version of volumetric MRI, with consequent advantages in SNR and slice-direction resolution.

Methods and Results

With a fairly potent control over cluster profiles of excited spins, MRI can create configurations for its spin excitation and signal acquisition stages to work more complementarily with one another, so as to better address certain imaging challenges.

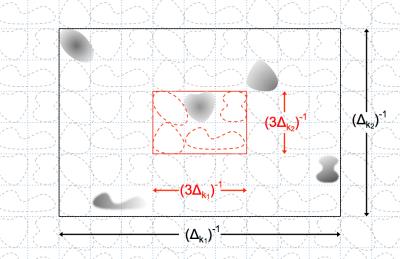
A packable configuration refers to one in which sub-Nyquest k-space sampling causes signal contributing clusters to fold or alias yet stay non-overlapped in a reduced FOV, as illustrated in Fig.1. One can exploit such a configuration to probe or sample an extensive area with a considerably lower cost than that required by the standard Nyquest rate. While the excitation control supplies cluster locations, the k-space sampling of the signal acquisition stage leads to finer details. It suffices for the latter to work with the packed FOV, hence coarser k-space sampling. The new technique may therefore provide much superior resolution or speed than a standard technique.

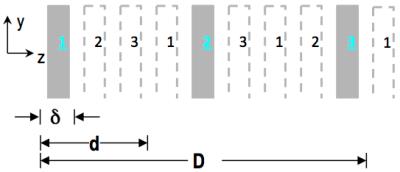
For multi-slice imaging the present technique treats it as an adapted volumetric MRI – it simultaneously excites N target slices that are fitted conceptually to organizing bins of a packable configuration (Fig.2), and acquires signals in accordance with the packed FOV (i.e., k_x-k_y-k_z sampling with considerable under-sampling along k_z but otherwise normal). For even k-space sampling cases, it reconstructs multiple slices with inverse Fourier transform. An intrinsic agility in terms of total number of spatial encodes is present since for separating the N slices along z, as few as N k_z sampling steps are needed. With the non-overlapping condition as the base, proper slice profiles and recon PSF jointly effect projections across short z-intervals, one for each individual slice, with negligible cross-talk amongst the projections. To improve z-direction spatial resolution beyond the slice thickness², the new technique employs P·N sampling steps to narrow the PSF and resolve P voxel across each δ interval, producing sub-slices of resolution δ/P. Compared to previous volumetric treatments of SMS^3,4, the packed FOV enables the new technique to offer considerably sharper PSF’s, at P=1 or larger – this is a key to enhancement of z-direction resolution.

Parallel receive acceleration, along all 3 dimensions simultaneously if desired, is applicable to the new SMS as it is to usual volumetric MRI. Fig.3 illustrates how to integrate parallel-receive acceleration by further reducing FOV from a packed-FOV base. Note that while the base is the packed FOV, the clusters being imaged through it carries receive sensitivities across the relatively extensive original FOV. This helps manage g-factor of parallel MRI when it reduces the FOV beyond the base. Incorporation of CAIPIRINHA-type phase modulation⁵ promises additional help, although not using it facilitates, for instance, maintaining CMPG condition for FSE, or use of PINS⁶ for SAR management.

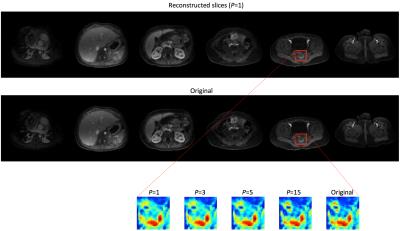
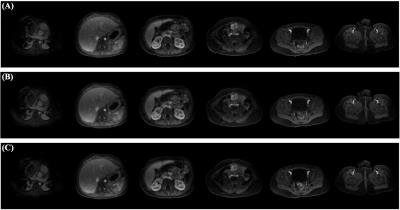
The new technique was tested in simulated imaging studies. One study used a volume data set obtained from 32-channel parallel MRI with spatial resolution of, respectively, 1.1mm, 1.0mm and 1.6mm along x(L/R), y(A/P) and z(S/I). A ~4mm-thick slice profile corresponding to a 90° SLR excitation pulse was used to emulate 6 excited slices that are orthogonal to z and with center-to-center spacing of 56mm. With 3x parallel-MRI z-acceleration, k_z-sampling had FOV_z=2δ=16mm and 2 steps, a reduction from packed-FOV=6δ=48mm and 6 steps. A 3x y-acceleration was simultaneously applied. Slice images reconstructed from the parallel MRI 3D k-space data matched well the original except for some z-direction blurring (Fig.4). Increasing P from 1 to 3, 5 and 15 improved the slice-direction resolution (Fig.4) and produced, at P=5, quality sub-slices of resolution approaching 1.6mm (Fig.5).

Discussion

This study suggested that, with a straightforward adaption of 3D k-space sampling, one may effectively accomplish not only SMS but sub-slice resolution. Note that the efficiency arises from FOV-packing, full benefit of 3D-encoding, and parallel-MRI acceleration. Other FOV-packing applications could be explored – FOV-packing maximizes efficiency mapping gapped distribution (spatially, spectrally and etc.) and extends reach. FOV-packing is compatible with many existing concepts and tools related to k-space.

Acknowledgements

We thank the researchers behind http://mridata.org for sharing volumetric data sets with the MRI community, including one that was used in the reported study.

References

1. Barth M, Breuer F, Koopmans PJ, Norris DG, Poser BA. Simultaneous Multislice (SMS) Imaging Techniques, Magn Reson Med 75:63-81, 2016.

2. Setsompop K, Bilgic B, Nummenmaa A, Fan Q, Cauley S.F, Huang S, Chatnuntawech I, Rathi Y, Witzel T, Wald LL. SLIce Dithered Enhanced Resolution Simultaneous MultiSlice (SLIDER-SMS) for high resolution (700um) diffusion imaging of the human brain. Proc ISMRM 2015, p. 339.

3. Zhu K, Kerr A, Pauly J. Autocalibrating CAIPIRINHA: reformulating CAIPIRINHA as a 3D problem. Proc ISMRM 2012, p. 518.

4. Zahneisen B, Poser BA, Ernst T, Stenger VA. Three-dimensional Fourier encoding of simultaneously excited slices: generalized acquisition and reconstruction framework. Magn Reson Med 71:2071–2081, 2014.

5. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med 53:684–691, 2005.

6. Norris DG, Koopmans PJ, Boyacioglu R, Barth M. Power Independent of Number of Slices (PINS) radiofrequency pulses for low-power simultaneous multislice excitation. Magn Reson Med 66:1234–1240, 2011.

Figures

Fig.1 FOV-packing Taking advantage of the gaps between clusters of excited spins in the standard FOV (black), sampling k-space much coarser than the Nyquest rate (e.g., 3x coarser than Δ_k1 and 3x coarser than Δ_k2, as shown) avoids overlaps amongst signals (actual as well as aliased), which in effect reduces the task of MRI’s signal acquisition stage to one of resolving the packed FOV (red).

Fig.2 SMS leveraging FOV-packing Three excited slices (turquoise-labeled) orthogonal to z, each conceptually occupying an organizing bin of depth δ, sample a volume of depth D=9δ. The packed FOV is of depth d=Nδ=3δ. At a sampling rate of 1/d (3x coarser than the Nyquest rate of 1/D), overlaps amongst signals (including aliased, black-labeled) remain absent. Imaging the three slices entails sampling k_z at -1/d, 0 and 1/d. Extending the width of k_z coverage with P·N (P>1) sampling steps narrows the PSF and resolves P voxel across each δ interval. This enables going beyond the slice thickness and resolving δ/P-thick sub-slices.

Fig.3 Further reduction of FOV beyond the packed-FOV with parallel receive acceleration Figure illustrates 3x acceleration in two 6-slice imaging examples where FOV is further reduced from the base of 6-bin deep (packed-FOV depth) to 2-bin deep. The number of k_z sampling steps is 2P (=P·N /z-direction acceleration factor). Much flexibility exists for configuring FOV packing and parallel receive.

Fig.4 Six-slice SMS with FOV-packing and 9x parallel-receive acceleration Simulation of parallel MRI k_x-k_y-k_z data used Cartesian sampling. Parameters for configuration included δ=8mm, P=1, packed-FOV depth=6δ=48mm, 3x z-direction acceleration yielding further reduction: FOV_z=2δ=16mm and 2 k_z-sampling steps, and 3x y-direction acceleration. The PSF-defined z-resolution is δ/P =8mm but the actual z-resolution is 4mm (slice thickness) at P=1. Slice images reconstructed from the data (A) and original cross-section images (1.6mm z-resolution) at same locations (B) are shown. Increasing P to 3, 5 and 15 (corresponding to 6, 10 and 30 k_z-sampling steps) improved the slice-direction resolution (C).

Fig.5 Sub-slices with resolution beyond the thickness of excited slices At P=5 the above 6-slice SMS case resolved 5 voxels across each δ interval. This led to creation of sub-slices that are of resolution δ/P =1.6mm. For each of the 4mm-thick excited slices Figure shows 3 sub-slices that are located at 1.6mm above (A), at (B), and 1.6mm below (C) the center. The z-direction spatial resolution broke through the constraint of the thickness of the excited slices.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

3970