3969
Evaluation of phase-cycled bSSFP for qMT mapping in the brain in off-resonance conditions1CISC, BSMS, Brighton, United Kingdom, 2Physics, University of Sussex, Brighton, United Kingdom
Synopsis
The balanced steady-state free precession acquisition approach is well-suited to quantitative magnetization transfer studies, owing to intrinsic MT weighting, rapid acquisition times and good SNR. However, the presence of off-resonance banding artefacts have limited its use, especially at B0>1.5T. This work is the first to evaluate a phase-cycled approach to bSSFP that can remove banding artefacts by taking maximum intensity projection MIP or taking a weighted mean as part of the qMT analysis. We conclude that neither MIP and weighted mean alone are capable of fully removing banding artefacts from qMT maps.
Aim
To evaluate the effectiveness of phase-cycled balanced steady-state free-precession (bSSFP) in the removal of off-resonance banding artefacts for qMT and consider the prospect of bSFFP qMT at B0>1.5 T.Introduction
Quantitative magnetization transfer (qMT) imaging is sensitive to the interaction of macromolecular and free water pools and can provide a window to subtle changes to tissue. The macromolecular component of tissue (assumed to be myelin in the white matter) cannot be detected with conventional MRI due to the short T2, but qMT can reveal important information about this component. In recent years bSSFP has been used to acquire qMT data capable of providing the bound proton fraction (F), the T2 of the free-water pool (T2f) and the forward MT rate constant (kf) in as little as 10 minutes1,2. This is much shorter than the classic gradient echo approach that typically takes 30 minutes3. However, the bSSFP technique is particularly sensitive to off-resonance effects that manifest as dark bands across the image where an off-resonance condition is met. This phenomenon worsens at higher field strengths and this has limited (or even prohibited) bSSFP qMT at B0 > 1.5 T. This work evaluates the method introduced by Deoni et al4,5 that combines bSSFP images acquired with different phase cycling applied to the RF pulse train that can greatly reduce (or even remove) this banding artefact. We test this method at 1.5 T using the shim coils to compare the performance of the method at optimum shim calibration with increasing off-resonance conditions.
Theory
In bSSFP, the phase of the RF pulse is incremented by $$$\Delta\phi=\pi$$$, since close to resonance a largely-homogeneous signal is acquired, but off-resonace where $$$\Delta\omega$$$t$$$\rightarrow\Delta\phi=\pi$$$ the signal is attenuated and dark bands appear in the image (Figure 1a)4. If RF phase $$$\Delta\phi=0$$$, the location of the banding artefacts is shifted such that the highest signal intensity is observed in the regions where $$$\Delta\omega$$$t$$$\rightarrow\pi$$$. We consider two methods: (i) calculating the maximum intensity projection (MIP) from $$$\Delta\phi=0$$$ and $$$\Delta\phi=\pi$$$ images4 and (ii) calculating the weighted mean of qMT parameters derived from a separate qMT analysis of $$$\Delta\phi=0$$$ and $$$\Delta\phi=\pi$$$ images.
Methods
Images were acquired on a Siemens Avanto 1.5 T imager, using the TrueFISP (bSSFP) pulse sequence. We acquired data under three conditions:
(i) optimum shim settings (~on-resonance)
(ii) increased y-shim (off-resonance)
(iii) strongly increased y-shim (extreme off-resonance).
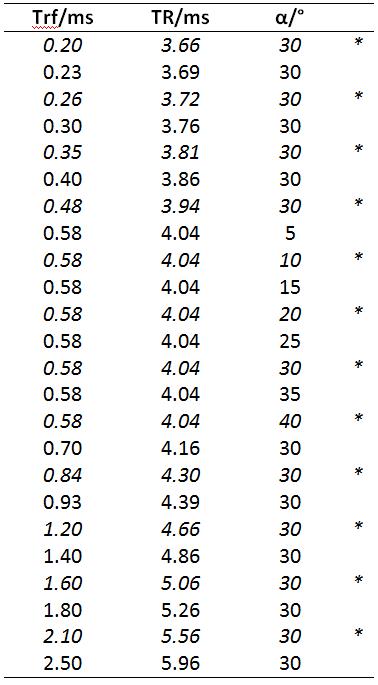
Acquisition parameters: matrix: 256x96, slices=32, slice thickness=5mm. For qMT, image volumes with different TR, RF pulse duration(Trf) and RF flip angle ($$$\alpha$$$) were collected (Table 1). Each volume was collected twice with RF phase increment $$$\Delta\phi=0$$$ and $$$\Delta\phi=\pi$$$. Total scan time: 20minutes.
MIP: MIPs were generated by taking the maximum signal intensity at each voxel location for corresponding volumes with $$$\Delta\phi=0$$$ and $$$\Delta\phi=\pi$$$. These MIPs were used to calculate the qMT parameters1. An abbreviated acquisition scheme, using only the italicized acquisition parameters in Table 1 was employed to explore the effect of reducing the total scan time to 10 minutes.
Weighted-mean: Data from the $$$\Delta\phi = 0$$$ and $$$\Delta\phi = \pi$$$ were analyzed separately to generate qMT parameter maps under each phase-cycling regime. Using the least-squares $$$\chi^2$$$ goodness-of-fit, a pixelwise weighted mean of the two data sets was calculated; where parameters with the best fit (lowest $$$\chi^2$$$) contributed most4.
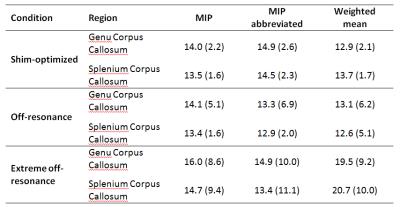
Region-of-Interest: mean F parameter from the genu and splenium of the corpus callosum was calculated for the MIP, MIP-abbreviated and weighted-mean techniques.
Results
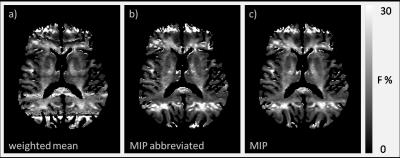
The MIP approach produced apparently artefact-free images for all 3 off-resonance conditions (Figure 1b). After fitting the qMT model, the MIP approach on shim-optimized data recovered data lost in frontal regions (Figure 2a, arrows) but in both the mild and extreme off-resonance conditions residual banding artefacts remained (Figure 2b,c). Residual banding artefacts were also observed with abbreviated-MIP and weighted-mean approach (Figure 3). Region-of-interest analyses revealed that F is over-estimated with all methods in the extreme off-resonance regime (Table 2) . The MIP approach gives similar F in the shim-optimized and off-resonance conditions, while the abbreviated-MIP and weighted-mean approaches tend to underestimate F.Discussion and Conclusion
This work is the first to evaluate the phase-cycled bSSFP approach to qMT. Importantly, this work revealed off-resonance effects can be effectively removed at 1.5 T to provide artefact-free qMT parameter maps. Crucially, however, under stronger off-resonance conditions (such as those at higher B0 field) we identified that significant artefacts remain in the qMT maps even when not readily observed in the MIP data. This study suggests that MIP or weighted mean approaches alone are not sufficient to provide artefact-free qMT data at B0>1.5 T, where off-resonance effects are appreciable.Acknowledgements
No acknowledgement found.References
(1) Gloor M, Scheffler K, Bieri O. Quantitative Magnetization Transfer Imaging Using Balanced SSFP. Magn. Reson. in Med. 60:691–700 (2008).
(2) Bieri O, Scheffler K. On the Origin of Apparent Low Tissue Signals in Balanced SSFP. Magn. Reson. in Med. 56:1067–1074 (2006).
(3) Dowell NG, van den Boomen H, Cercignani M. Comparison of SSFP and GRE sequences for qMT acquisition. Proc. Intl. Soc. Mag. Reson. Med. 21 4284 (2013).
(4) Deoni SCL, Ward HA, Peters TM, Rutt BK.Rapid T2 Estimation With Phase-Cycled Variable Nutation Steady-State Free Precession. Magn. Reson. in Med. 52:435– 439 (2004).
(5) Deoni SCL. Transverse Relaxation Time (T2) Mapping in the Brain With Off-Resonance Correction Using Phase-Cycled Steady-State Free Precession Imaging. J. Magn. Reson. Imaging 30:411– 417 (2009).
Figures
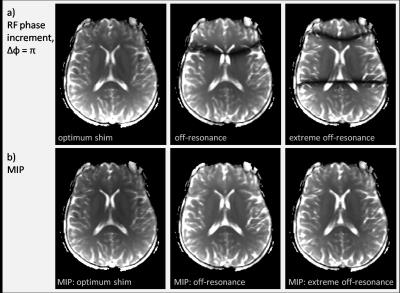
Figure 1 – representative axial slice from (a) bSSFP of the brain and (b) intensity projections (MIPs) generated from phase-cycled bSSFP ($$$\Delta\phi=0, \Delta\phi=\pi$$$). Under the scanner-optimized shim setting off-resonance artefacts are only present at the edges of the brain in the bSSFP images; with increased y-shim current an off-resonance band through the centre of the brain is observed; increasing y-shim currents further produce 2 banding artefacts (extreme off-resonance condition). The banding artefacts are apparently removed in the MIPs for each of the three resonance conditions.