3958
Triple Quantum Filtering in Sodium Magnetic Resonance Imaging Using Strongly Modulated Pulses1Institut of Neuroscience and Medicine - 4, Forschungszentrum Jülich GmbH, Jülich, Germany, 2Department of Neurology, Faculty of Medicine, JARA, RWTH Aachen University, Aachen, Germany
Synopsis
23Na-MRI can be used for non-invasive investigation of metabolic disease, based on discrimination between sodium signals arising from different tissue compartments due to development of multiple quantum coherences mainly in intracellular space. Strongly modulated pulses in NMR and MRI can be created using optimal control design to generate the most efficient transfer between the initial and target states of the nuclear spin ensemble, defined by the density matrix formalism. The Krotov algorithm and its implementation by Maximov of the optimal control design were used to modify the first hard RF pulse in the SISTINA sequence.
Purpose
23Na-MRI used for non-invasive investigation of
metabolic disease is based on discrimination between sodium signals created in
different tissue compartments. The separation between intra- and extracellular
space is possible using triple quantum filtering (TQF), which makes use of the
fact that multiple quantum coherences (MQCs) mainly evolve in intracellular
space. The standard TQF sequence however is time consuming due to multiplex
phase cycling with a minimum of 6 steps and multiple averages1. It
also produces high SAR due to the application of three hard RF pulses. Strongly
modulated pulses can be created using optimal control design2,3 to generate the most efficient transfer between the initial
and target states of the nuclear ensemble, defined by the density matrix
formalism. The Krotov algorithm4 and Maximov implementation2,3 of the
optimal control design are used in this research to modify the sequence in
order to reduce SAR and induce optimal state transfer. Methods
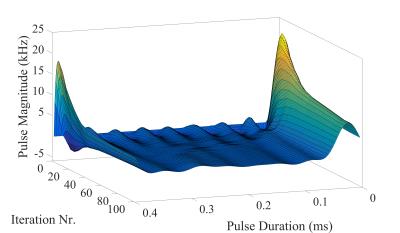
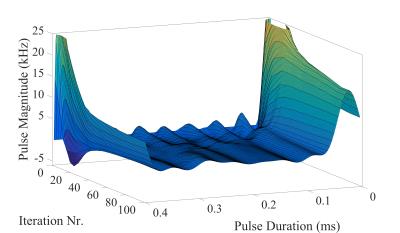
Simulations: The SISTINA sequence5 is an improved modification of the TQF, which allows simultaneous creation and measurement of single-quantum coherences (SQCs) and triple-quantum coherences (TQCs). SISTINA consists of three RF pulses with preparatory time τ and a single ultra-short echo time UTE read-out between the first and the second pulse for measuring SQCs, and evolution time δ between the second and the third pulse, followed by Cartesian read-outs for measuring TQCs. The evolution of the ensemble of nuclear spin-3/2 during sequence performance is fully described by density matrices and is calculated with MATLAB6 for any given time. Usually the transfer between the states in a quantum system is provided through hard RF pulses. However, strongly modulated pulses (SMP) can be used instead. SMP induce the transfer between states with higher efficiency, which is given by the quality function, calculated as an overlap between the desired state and the achieved state, with energy deposition being the penalty factor. The search of the optimal solution of the problem is performed using the Krotov algorithm, with the control parameter being pulse amplitude. In this research, the method2,3 is adapted to sodium imaging with the SISTINA sequence. The dynamics of the system is given by the Liouville von Neumann equation, with the Hamilton operator defined as:
$$\hat{H}(t)=\hat{H}_{0}+\sum_{k=x,y}\omega_{1k}(t)\hat{I}_{k}$$
It describes the behaviour of the ensemble during the RF pulse with duration T, with $$$\omega_{1k}(t)$$$ - characteristic time dependent amplitude of the RF pulse. Here the influence of the static quadrupole Hamiltonian is investigated. For the simulations the asymmetry parameter in the unordered biological tissue is $$$\eta=0$$$, so that the governing Hamiltonian during the pulse is given by:
$$\hat{H}_{0}=\frac{\omega_{Q}}6\cdot[2\hat{I}_{z}^{2}-\hat{I}_{x}^{2}-\hat{I}_{y}^{2}]$$
The starting point for the optimization is a rectangular pulse with amplitude $$$\omega_{1x}=3925$$$ Hz, $$$\omega_{Q}=60$$$ Hz2,3.
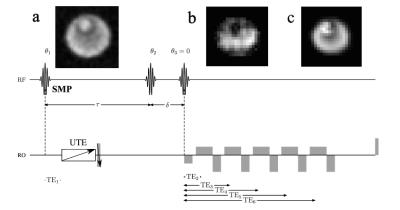
Experimental Conditions and Measurement Parameters: Phantom experiments were performed on a home-built, small-bore 9.4T scanner using a Siemens console with a home-built, single-tuned Na coil, using a 64cmx64cmx32cm field-of-view with 0.1cm isotropic resolution. A 12-step phase cycle was implemented with 2 averages and a repetition time of TR = 150ms yielding a measurement time of approx. 24min. A preparatory time is τ = 7000µs, the evolution time is δ = 40µs. A UTE readout was performed at TEUTE = 0.7ms using the DISCOBALL7 scheme. A Cartesian readout was performed at 5ms after the third RF pulse. The phantom consisted of two cylindrical tubes with diameters of 30mm and 11mm, whereas the small tube was filled with NaCl water solution, the larger tube was filled with agarose gel mixed with NaCl of the same concentration.
Results
The optimized first RF pulse in the initial SISTINA sequence was calculated for each phase cycling step. The example of a first SMP generated for the first phase cycling step is presented in Fig. 1. Time evolution of the pulse amplitudes is presented in Fig. 2 and Fig. 3. The resulting images from the UTE readout, and both Cartesian readouts are presented in Fig. 4. The images from both tubes acquired with the UTE readout are sodium concentration weighted and are comparable because of equal sodium concentration. The Cartesian readout with appropriate post-processing delivers two contrasts: one is triple quantum weighted with higher signal from the large tube; the second is single quantum weighted with higher signal from the small tube.Conclusion
The simulated SMPs for 12 phase cycling steps are implemented in the initial SISTINA sequence and allow simultaneous acquisition of three contrasts with the expected contrast. This makes the method superior to standard TQF due to optimized state transfer and builds a basis for further implementation of SMPs in the SISTINA sequence.Acknowledgements
The authors thank Nadine Rosen for the help with phantoms, Klaus Möllenhoff for the help with sequence programming and Chang-Hoon Choi for the coils.References
1. Ivchenko N, et al. Multiplex phase cycling. J.Magn. Reson. 2003; 160: 52–58.
2. Maximov I, et al. Optimal control design of NMR and dynamic nuclear polarization experiments using monotonically convergent algorithms. J. Chem. Phys. 2008; 128.18: 184505.
3. Maximov I, et al. A smoothing monotonic convergent optimal control algorithm for nuclear magnetic resonance pulse sequence design. J. Chem. Phys. 2010; 132.8: 084107.
4. Krotov V, Global methods in optimal control theory. CRC Press, 1995; Vol. 195.
5. Fiege D.P, et al. Simultaneous Single-Quantum and Triple-Quantum- Filtered MRI of 23Na (SISTINA). Magn Reson Med 2013; 69:1691–1696.
6. MATLAB and Statistics Toolbox Release 2015b, The MathWorks, Inc., Natick, Massachusetts, United States.
7. Stirnberg R, et al. A new and versatile gradient encoding scheme for DTI: a direct comparison with the Jones scheme. Proc Int Soc Mag Reson Med 2009; 17:3574.
Figures