3957
High-resolution 3D T2 mapping using a stack-of-stars radial FSE pulse sequence1Electrical and Computer Engineering, University of Arizona, Tucson, AZ, United States, 2Medical Imaging, University of Arizona, Tucson, AZ, United States
Synopsis
T2 mapping is a parametric imaging approach that provides quantification of T2-weighted images for a more accurate diagnosis of pathology. 2D multi-slice T2 estimation techniques cannot be used for thin slice isotropic imaging. To overcome this limitation, we present a T2 mapping technique using a 3D radial FSE pulse sequence with a variable flip angle scheme for optimal T2-weighting and T2 mapping within SAR constraints. Data is acquired in a stack-of-stars radial trajectory and T2 maps are reconstructed using model based iterative algorithms. The method is demonstrated in phantoms and in vivo brain and musculoskeletal imaging.
Introduction
T2-weighted imaging is widely used in the clinic for tissue characterization. T2 mapping is a parametric imaging approach that provides quantification of T2-weighted images for a more accurate diagnosis of pathology. T2 mapping involves acquiring data at multiple TE times to obtain the T2 map. A 2D radial fast spin-echo technique has been developed for fast T2 mapping by taking advantage of the oversampling of the k-space center with radial trajectories1,2. However, 2D multi-slice imaging techniques cannot be used for thin slice isotropic imaging. To overcome this limitation, we presented3 an approach for isotropic T2 mapping using a 3D radial fast spin-echo technique based on the stack-of-stars trajectory. The method enabled the reconstruction of 3D volumes at multiple TEs and the corresponding T2 maps with isotropic spatial resolution. The technique was based on constant refocusing flip angles thus, suffered from (i) signal loss through the long echo trains and (ii) long TRs in order to comply with SAR limits. In this work, we present a T2 mapping technique using a 3D radial FSE pulse sequence with a variable flip angle (varFA) scheme for optimal T2-weighting and T2 mapping within SAR constraints.Technique
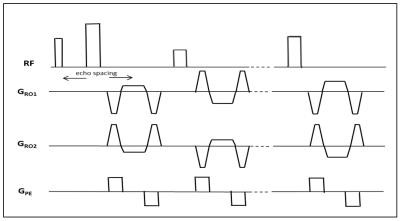
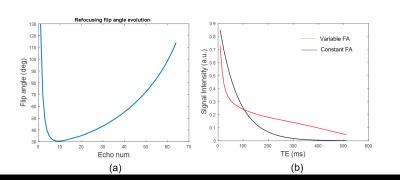
A 3D Cartesian FSE pulse sequence was modified to support a stack-of-stars trajectory where each kz plane contains radial views corresponding to multiple TE points (Fig.1). A varFA design based on a 3 flip angle parameter approach4 was implemented. The refocusing flip angles were optimized to maximize the area under the T2 decay curve (for improved overall SNR) and minimize SAR. Figure 2 shows (a) the flip angle scheme and (b) effect of the flip angle modulation on the signal intensity compared to a constant flip angle scheme.
To achieve fast imaging, data for each TE point is highly under-sampled (3 views/TE per kz plane). Thus, 3D TE images are reconstructed using sparsity-based iterative reconstruction algorithms. Previously our group had proposed1 a principal component (PC) based T2 mapping technique with indirect echo compensation for 2D radial FSE data based on the slice-resolved extended phase graph model. For 3D T2 mapping, the reconstruction problem is written as:
$$argmin_{I_0,T2,T1,B1} \sum_{j=1}^{ETL}||FT_j\{C_j(I_0,T2,T1,B1,TR,\alpha_0,\ldots,\alpha_j)\} - K_j||_2^2$$
where $$$FT_j$$$ is the Fourier operator, $$$K_j$$$ is the undersampled k-space data at the jth TE, $$$C_j$$$ is the EPG signal model as a function of I0, T2, T1, B1, TR and the flip angles of the excitation and refocusing RF pulses. The signal model is linearized using a PC basis generated from a set of training curves. The linearized problem is expressed as:
$$argmin_{M}\sum_{l=1}^{coils}\sum_{j=1}^{L}||FT_j\{S_lMP_j^T\} - K_{l,j}||_2^2 + \lambda ||\psi M||_1$$
where $$$P$$$ is a matrix of the first principal components, $$$M$$$ is a matrix corresponding to the PC coefficients, $$$S_l$$$ are the complex coil sensitivities. The penalty term exploits the spatial compressibility of the PC coefficient maps using a sparsity transform $$$\psi$$$. The images at $$$TE_j$$$ are obtained using the $$$L$$$ PC coefficients as $$$MP_j^T$$$ , where $$$P_j$$$ is the jth row of the matrix $$$P$$$. T2 maps are estimated by using a pattern recognition technique3 using pre-computed dictionaries based on the EPG model.
Methods
T2 mapping accuracy was tested at 3T using a set of gel phantoms with different T2 values. The reference T2 estimates were obtained using a 2D single-echo spin-echo (SE) sequence since this method is not affected by indirect echoes. In vivo knee data were acquired on a healthy volunteer using the 3D radial FSE sequence with TR=1.2sec, ETL=64, FOV=17cm, base resolution=256, radial views=192 and 1mm thick slices. 1.1 mm isotropic resolution brain data were acquired with ETL=96, TR=1.5sec, FOV=28cm, base resolution=256, and 288 radial views.Results
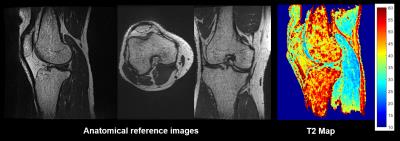
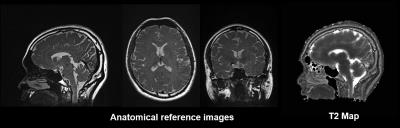
Figure 3 shows results from the phantom validation experiments. Note that the mean T2 estimates using the 3D radial FSE sequence are similar to those from the SE reference. Images of the knee in the three orientations together with the T2 map for the sagittal view for a normal volunteer are shown in Figure 4. Figure 5 shows axial, coronal and sagittal cross sectional images of the brain along with the T2 map (only the sagittal plane is shown).Conclusion
A 3D T2 mapping technique based on the 3D radial FSE sequence with variable refocusing flip angles is presented. Phantom experiments show that the estimated T2 values are comparable to the SE sequence. The technique provided excellent coverage of the anatomy of interest with high spatial resolution within clinically acceptable times (~ 7min). The variable flip angle maintains the signal above the noise level throughout the long ETL for optimal T2 mapping and keeps SAR within acceptable limits.Acknowledgements
No acknowledgement found.References
1. Huang C., Bilgin A., Barr T., Altbach M, T2 relaxometry with indirect echo compensation from highly undersampled data, Magnetic Resonance in Medicine, 70(4) 2013
2. Altbach M., Bilgin A., Li Z., Clarkson E., Trouard T., Gmitro A., Processing of radial fast spin-echo data for obtaining T2 estimates from a single k-space data set, Magnetic Resonance in Medicine, 54 2005
3. Keerthivasan MB, Bilgin A, Martin DR, Altbach MI. Isotropic T2 mapping using a 3D radial FSE (or TSE) pulse sequence. In Proceedings of ISMRM, Vol. 23, Toronto, Ontario, Canada, 2015. p. 323
4. Busse RF, Brau ACS, Vu A, Michelich CR, Bayram E, Kijowski R, Reeder SB, Rowley HA. Effects of refocusing flip angle modulation and view ordering in 3D fast spin echo. Magn Reson Med 2008;60: 640–649
5. Huang C., Altbach M, Fakhri G., Pattern recognition for rapid T2 mapping with stimulated echo compensation, Magnetic Resonance Imaging, 32, 2014
Figures