Synopsis

An ellipse fitting approach has been recently proposed for simultaneous estimation of the relaxation times T₁ and T₂ from phase-cycled balanced steady-state free precession (PC-bSSFP). In this work we present an analysis of the SNR sensitivity of the proposed method and optimization of the sequence parameter settings. We demonstrate, that it is feasible to perform an accurate and precise T₁ and T₂ mapping while using an optimal FA and TR combination for realistic SNRs.

Purpose

Methods

The elliptical signal model was used to describe the complex PC-bSSFP steady-state signal [2,3] :

$$I=M_{eff} \frac{1-ae^{i\theta}}{1-b\cos\theta}e^{i\Omega TE},$$where $$$M_{eff}=M\exp{(-\frac{TE}{T_{2}})}$$$, $$$M=\frac{M_{0} (1-E_{1}) \sin\alpha}{1-E_{1}\cos\alpha-E_2^2 (E_{1}-\cos\alpha)}$$$, $$$a=E_{2}$$$, $$$b=\frac{E_{2}(1-E_{1})(1+\cos\alpha)}{1-E_{1}\cos\alpha -E_2^2 (E_{1}-\cos\alpha)}$$$, $$$E_{1}=\exp(-\frac{TR}{T_{1}})$$$, $$$E_{2}=\exp(-\frac{TR}{T_{2}})$$$, M₀ - the equilibrium magnetization, α - the flip angle, TR - the repetition time, θ - the resonance offset angle, θ = θ₀ + ∆θ, θ₀ = 2π(δ_CS+Δf₀), ∆f₀ - the off-resonance, caused by local field deviations, δ_CS - the chemical shift of the species with respect to water, ∆θ - the user controlled RF phase increment.

To investigate the optimal choice for FA and TR, Monte Carlo simulations were performed (Matlab R2015a) for a range of FA 0-90˚ and TR 0-50 ms for the initial settings: M₀ = 10000, T₁ = 675 ms, T₂ = 75 ms, ∆f₀ = 0, δ_CS = 0, 10 phase cycles with phase increments $$$∆\theta_{n}=\frac{2\pi n}{10}, n=\left\{0,1...9\right\}$$$. The chosen T₁ and T₂ represent white matter. Gaussian noise with a standard deviation σ = 16 was added to the complex data, resulting in an SNR range 30-100. The accuracy of the method was assessed by calculating the absolute errors in T₁ and T₂ estimates.

The SNR was defined as $$$SNR=\frac{\sum_{n=1}^N \mid I_{n}(\theta)\mid}{N\sigma}$$$, as proposed by Björk et.al. [4], with $$$\mid I_{n}(\theta)\mid$$$ - the magnitude of n^th phase-cycled image, N - the total number of phase cycles, σ – the standard deviation of noise in each bSSFP acquisition.

The precision of the method was assessed by calculating the standard deviation of T₁ and T₂ estimates. The minimum SNR required to obtain a 5% precision, was calculated for the same initial parameter settings and the found optimal combination of TR and FA.

MRI experiments on a phantom (TO5, Eurospin II test system, Scotland) and in vivo (brain of healthy volunteer) were performed on a clinical 1.5T MR scanner (Philips Ingenia, Best, The Netherlands). A 16-channel head receive coil was used. Sequence parameter settings: 3D bSSFP, FOV 220x220x80 mm³, voxel size 1.5x1.5x4 mm³, TR 10 ms, FA 20˚, 10 phase cycles.

Results

Figure 1 provides the absolute errors in T₁, T₂ and corresponding SNR values for different FA-TR combinations. The green area corresponds to “favorable combinations” of FA and TR, where the absolute errors in T₁ and T₂ are less than 5 ms (for T₁) and 0,5 ms (for T₂), which gives an accuracy of 1% .

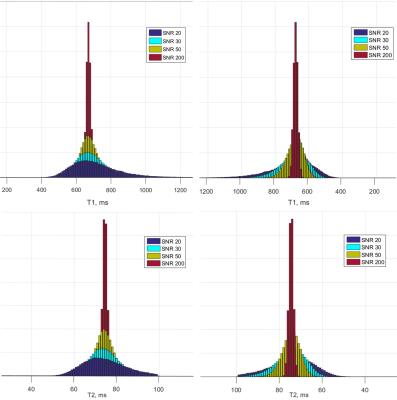
Figure 2 demonstrates the distribution of T₁ and T₂ estimates for different SNR in histograms for the optimal combination of FA and TR and the same initial parameter settings. The peaks become narrower and more symmetrical with increasing SNR, while a bias exists for low SNR.

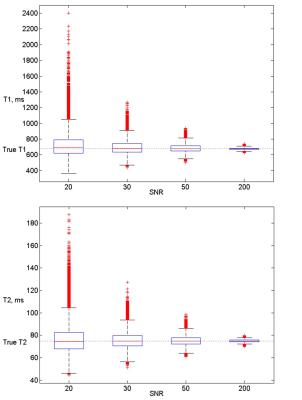
Figure 3 demonstrates the distribution of T₁ and T₂ estimates for different SNR. The interquartile range (IQR) becomes smaller with the SNR increasing and the median values approaches the true values of T₁ and T₂.

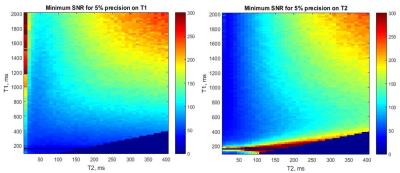
Figure 4 shows the minimum required SNR to achieve a 5% precision in T₁ and T₂ estimation. For white matter the minimum SNR is 75 and for gray matter it is 100.

Figure 5 presents experimental results for the phantom and in vivo.

Discussion and Conclusion

Acknowledgements

References