3947
Motion-Robustness Evaluation and Motion Correction of Wave-Encoding1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States, 3Global MR Applications and Workflow, GE Healthcare, Houston, TX, United States
Synopsis
The motion-robustness of a 3D wave-encoded SPGR sequence was evaluated by simulating the acquisition of a Gaussian-profile object with periodic motion. Compared with non-wave-encoded sampling, wave-encoding provides better motion property because of wider diffusion of motion artifacts. A motion-correction method was also proposed for wave-encoding based on 3D translational motion estimates. This motion-correction method is demonstrated to effectively reduce motion artifacts in wave-encoded scans.
Purpose
Wave-encoding can improve the performance of highly accelerated parallel MRI by incorporating coil sensitivity variations in both phase-encoding (PE) and readout directions, and has been successfully applied in brain imaging1. Recently, a motion-robust auto-calibrating Wave-CS technique has been proposed, with potential applications in abdominal and pelvic imaging2. This technique avoids acquiring a separate calibration scan for coil sensitivity estimation, and is therefore robust to inter-scan subject motion. However, intra-scan motion may still degrade image quality. This study aims (1) to evaluate theoretically the motion-robustness of wave-encoding, and (2) to correct for intra-scan motion in wave-encoded scans using 3D translational motion correction.Methods
Evaluation of motion-robustness of wave-encoding
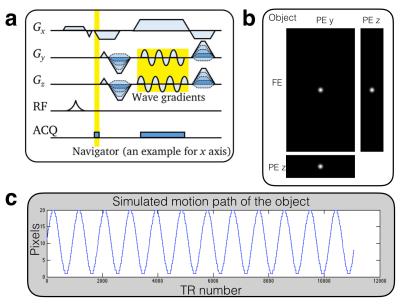
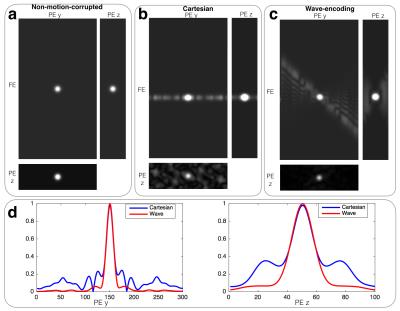
A 3D wave-encoded SPGR acquisition (Fig. 1a) was simulated to evaluate theoretically the motion property of wave-encoding. The wave-encoding gradient parameters used for simulation were 8mT/m amplitude and 7 cycles of sinusoids. A Cartesian acquisition was also simulated for comparison. An object with a Gaussian profile (Fig. 1b) was simulated with periodic motion in the frequency-encoding (FE) direction (Fig. 1c). VDRad3 Cartesian sampling ordering was used in the simulation. Images were obtained through inverse Fourier transform of the simulated fully-sampled k-space with simulated motion, and off-peak motion artifacts were estimated based on the cross-sectional images.
Motion correction of wave-encoded k-space
As demonstrated previously1, the wave-encoded signal and the Cartesian signal have the following relation in the kx-y-z domain: $$S_\text{wave}[k_x,y,z] =PSF[k_x,y,z]\cdot S_\text{Cartesian}[k_x,y,z]$$ and $$PSF[k_x,y,z] = \exp(-i\gamma\int_0^{t[k_x]}(g_y(\tau)\cdot y + g_z(\tau)\cdot z)d\tau)=\exp(C_1\cdot y + C_2\cdot z)$$ where C1 and C2 are constants associated with gradients gy and gz, and y and z are positions in image space.
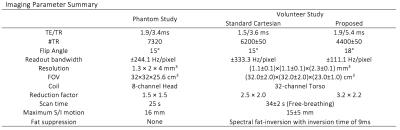
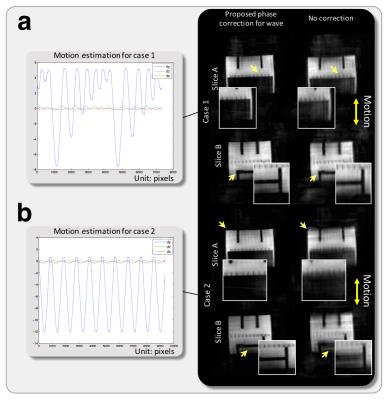
Linear-phase correction based on 3D translational motion estimates is proposed to correct each readout of the motion-corrupted wave-encoded k-space respectively. The relation between the motion-corrupted wave-encoded k-space signal Sm and the motion-corrected wave-encoded k-space signal S0 for a time point n can be expressed as: $$S_0[n]=S_m[n]\exp(-i2\pi(k_{x}[n]d_{x}[n]+k_y[n]d_{y}[n]+k_z[n]d_{z}[n]))\cdot\exp(C_1d_{y}[n]+C_2d_{z}[n])$$ where dx, dy, and dz are the estimated distance of linear translation in three orthogonal directions, and $$$\exp(C_1d_{y}[n]+C_2d_{z}[n])$$$ compensates for phase shifts due to linear translation of the wave-encoding PSF. To evaluate the performance of the derived motion-correction equation, one phantom study and two volunteer studies were conducted with Institutional Review Board approval and informed consent. Butterfly navigators4 were used to estimate the distance of translational motion, and VDRad sampling ordering3 was used in both scans. The imaging parameters for phantom study and volunteer scans were shown in Fig. 2. In volunteer scans, 8mT/m wave-encoding gradients with 7 cycles of sinusoids were used. Auto-calibrated estimation of coil sensitivity maps via ESPIRiT5, and CS-SENSE image reconstruction6 with L1-wavelet regularization were incorporated to reduce aliasing artifacts. Prior to reconstruction, acquired signals of each readout were corrected with the proposed motion-correction equation according to the corresponding motion estimates. Two free-breathing volunteers were scanned on a 3T scanner (GE MR750, Waukesha, WI) using a 32-channel torso coil (NeoCoil, Pewaukee, WI) with FE in S/I. Conventional Cartesian acquisitions with the same sampling pattern, scan time, and reconstruction framework were performed for comparison in the volunteer scans.
Results
As shown in Fig. 3, wave-encoding diffuses motion artifacts more widely than conventional Cartesian acquisitions in the 3D space in the simulation. It also yielded a better object profile with fewer surrounding artifacts in the PEy-PEz plane (Fig. 3a-c). The average magnitude of off-peak motion-corrupted pixels was 6.4% of the peak magnitude in the Cartesian case, and 3.0% in the wave-encoded case. In the 1D cross-section plots (Fig. 3d), wave-encoding yielded lower motion-induced side-lobes than the Cartesian approach.
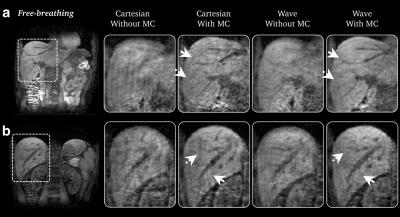
In the phantom study, the derived motion-correction equation reduced blurring from the original images without motion correction (Fig. 4). In volunteer scans, wave-encoding yielded slightly better images with less blurring than Cartesian acquisitions without motion-correction (Fig. 5). Better structural delineation and less motion artifacts were observed using the proposed motion-corrected wave-encoding approach (Fig. 5), compared with the conventional motion-corrected Cartesian approach.
Discussion
Wave-encoding achieves better parallel imaging performance than conventional Cartesian imaging with more efficient use of coil sensitivities through voxel spreading along the FE direction. When there is intra-scan motion, this voxel spreading effect leads to better motion robustness than the Cartesian approach. In combination with the derived motion-correction equation, a 3D wave-encoded SPGR sequence can improve image quality in free-breathing abdomen scans without increasing scan time.Conclusion
In this work, wave-encoding is demonstrated to provide better motion property than Cartesian in 3D SPGR sequence with VDRad sampling ordering4. A motion-correction method based on 3D translational motion estimates is proposed and demonstrated to effectively reduce motion artifacts in wave-encoded scans.Acknowledgements
GE Healthcare, NIH R01EB009690, NIH R01EB019241, NIH P41EB015891, Tashia and John Morgridge Faculty Scholars Fund.References
[1] Bilgic B, Gagoski BA, Cauley SF, Fan AP, Polimeni JR, Grant PE, Wald LL, Setsompop K. Wave-CAIPI for highly accelerated 3D imaging. Magnetic Resonance in Medicine. 2015; 73: 2152-2162.
[2] Chen F, Zhang T, Cheng JY, Pauly JM, and Vasanawala SS. Auto-Calibrating Wave-CS for Motion-Robust Accelerated MRI. Proc. Intl. Soc. Mag. Reson. Med. 2016; 24: 1857.
[3] Cheng JY, et al. Free-breathing pediatric MRI with nonrigid motion correction and acceleration, Journal of Magnetic Resonance Imaging. 2014, 42(2): 407-420.
[4] Cheng JY, Alley MT, Cunningham CH, Vasanawala SS, Pauly JM, Lustig M. Nonrigid motion correction in 3D using autofocusing with localized linear translations. Magnetic resonance in medicine 2012; 68:1785-1797.
[5] Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly J, Vasanawala SS, Lustig M. ESPIRiT - An Eigenvalue Approach to Autocalibrating Parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med 2014; 71:990-1001.
[6] Curtis A, Bilgic B, Setsompop K, Menon RS, Anand CK. Wave-CS: Combining wave encoding and compressed sensing. Proc. Intl. Soc. Mag. Reson. Med. 2015; 23: 0082.
Figures