3944
Accurate High-speed 3D-Registration of EPI vNavs for Head Motion Correction1John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, United States, 2Athinoula A. Martinos Center for Biomedical Imaging, Radiology Department, Massachusetts General Hospital, Charlestown, MA, United States, 3Department of Radiology, Harvard Medical School, Boston, MA, United States, 4Department of Radiology, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, United States
Synopsis
Low-resolution, whole-head volumes can be acquired rapidly with EPI-based volumetric navigators (vNavs). vNavs interspersed in a longer scan are widely used for prospective motion correction in a variety of sequences. To further improve the accuracy and flexibility of vNavs, we present a novel registration algorithm, tailored specifically for the vNavs application. Accuracy of the algorithm is tested on navigator volumes acquired with human volunteers at three isotropic resolutions, 6.4mm, 8mm, and 10mm, using a series of field of view (FOV) rotations and translations to provide ground truth rigid “motion”.
Purpose
Volumetric navigators (vNavs)1,2, based on 3D-encoded gradient echo EPI, are widely used prospective motion correction systems for neuroimaging, particularly in pediatric imaging. Previous applications of vNavs used the PACE3 registration algorithm, designed for higher-resolution fMRI volumes, constraining vNav design choices. In this work, we present a novel registration algorithm, achieving both the accuracy and efficiency requirements of prospective motion correction with lower-resolution, and thus faster, vNavs than PACE allowed.Method
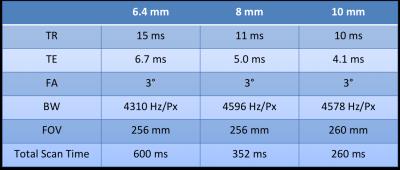
Imaging was performed on a 3 T TIM Trio (Siemens Healthcare, Erlangen, Germany), using the body coil to ensure spatial uniformity. Three human volunteers, having given informed consent, were scanned at three isotropic resolutions, 6.4 mm, 8 mm, and 10 mm (see acquisition parameters in Table 1).
Motion was simulated by a programmed series of FOV rotations and translations. “Small rotations” data contained a volume at iso-center and on-axis (the “reference”), followed by volumes with rotations of 0.5°-5° at 0.5° increments and translations of 1-5 mm at 1 mm increments. “Large rotations” data was acquired on two of the volunteers with rotations of 5°- 25° at 5° increments. Rotations were repeated around the x-, y-, and z-axes paired with z-direction translations, and around axes oriented along xy, xz, and yz paired with xy-direction translations. Scans were acquired in <30 s sets, during which the volunteers were instructed to hold their breath and remain still. 432 volumes per resolution per subject were acquired, from which 420 pairs (comparing each set’s “reference” with subsequent volumes) were extracted.
The volumes were masked before registration with a spherical mask (radius = image width/2 – 1 pixels) in the Fourier domain. Corners of the mask were Hann windowed to reduce ringing artifacts.
Our algorithm registers a new volume $$$V_N(\boldsymbol{x})$$$ to a given reference volume $$$V_R(\boldsymbol{x})$$$ by minimizing the residual
$$r(\boldsymbol{p}) = |\{\boldsymbol{W}(T(\boldsymbol{p}, \boldsymbol{x}))[V_N(\boldsymbol{x})-V_R(T(\boldsymbol{p}, \boldsymbol{x}))]|\boldsymbol{x}\in \boldsymbol{X}\}|_2,$$
where $$$T(\boldsymbol{p}, \boldsymbol{x})$$$ is a rigid transformation parameterized by $$$\boldsymbol{p} \in R^6$$$. $$$\boldsymbol{W}(\boldsymbol{x})$$$ is the same mask function initially applied in the Fourier domain, and $$$\boldsymbol{X}$$$ is the set of points inside our image FOV. We transform the reference to the new volume, interpolating only the reference volume. We can then precompute the coefficients of the cubic B-spline interpolator, accelerating each interpolation step4,5.
We performed Gauss-Newton minimization, giving the update equation $$\frac{\text{d}r(\boldsymbol{p})^T}{\text{d}\boldsymbol{p}}\frac{\text{d}r(\boldsymbol{p})}{\text{d}\boldsymbol{p}}\delta \boldsymbol{\boldsymbol{p}} = -\frac{\text{d}r(\boldsymbol{p})^T}{\text{d}\boldsymbol{p}}r(\boldsymbol{p})$$
We update our estimated $$$\boldsymbol{p}$$$ by composing its transformation with that given by $$$\delta \boldsymbol{p}$$$. A line search scales $$$\delta \boldsymbol{p}$$$, ensuring the residual decreases at each step. Minimization stopped when updates move all points in a 100 mm radius of the image center less than 0.05 mm.
We evaluate the gradient with the approximation
$$\frac{\text{d}r(\boldsymbol{p})}{\text{d}\boldsymbol{p}} \approx -\boldsymbol{W}(T(\boldsymbol{p},\boldsymbol{x}))\frac{\text{d}V_N(\boldsymbol{x})}{\text{d}\boldsymbol{x}}\boldsymbol{M}(\boldsymbol{x}),$$
where $$\boldsymbol{M}(\boldsymbol{x})=\begin{bmatrix}1&0&0&0&x_z&-x_y \\0&1&0&-x_z&0&-x_x\\0&0&1&x_y&-x_x&0 \end{bmatrix},$$
and $$\boldsymbol{x} = \{x_x, x_y, x_z\}.$$
We computed the “residual error transformation” between the estimated transformation and the known true transformation of each reference/new pair. We computed the RMS displacement that the “error transformation” would produce in a 100 mm sphere centered at isocenter6.
Results and Discussion
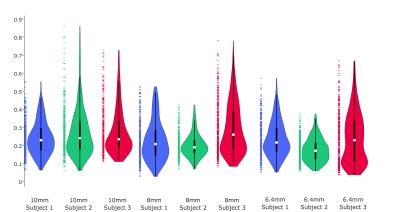
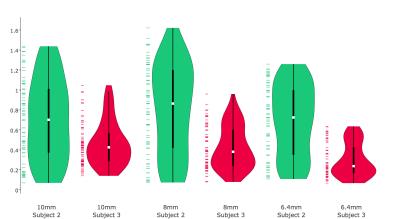
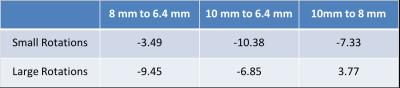
In all conditions RMS error was within 1 mm, with the exception of large rotations for one subject at 8mm resolution (Detailed results in Figures 2 and 3). We compared vNav resolutions using the Wilcoxon signed-rank test on the RMS errors (Results in Table 2). While 6.4 mm resolution produced the highest accuracy, assuming our motion tracking goal is ~1 mm, our new algorithm achieved functionally equivalent accuracy with 10 mm vNavs, requiring less than half of the acquisition time of 6.4 mm vNavs.
The algorithm is implemented in C++, using the Eigen7 library and is available on Github8. Median registration times for small rotations, running single-threaded on a 2.30 GHz Intel Xeon, were 12.97 ms, 25.10 ms, and 54.53, ms for 10 mm, 8 mm, and 6.4 mm vNavs respectively. Large rotations took 18.30 ms, 36.46 ms, and 88.47 ms, respectively.
To ensure that involuntary motion did not dominate registration error, we performed the same tests using a pineapple. Median RMS error in human subjects were 0.18, 0.14, 0.12, and in pineapple were 0.23, 0.21, 0.19, at 10 mm, 8mm and 6.4 mm resolutions, respectively.
Conclusions
We have developed and validated novel registration algorithm for vNavs that achieves fast and highly accurate motion tracking on a wider range of vNav protocols than was previously possible. Our algorithm supports motion correction with 10 mm vNavs, reducing navigator durations compared to previous designs, and increasing the number of sequences in which vNavs can be inserted.Acknowledgements
This work was funded by NIH awards: R00HD074649, R21AG046657, R01HD071664, R21EB008547, P41RR014075, R01HD085813 , K01DK101631, and the BrightFocus Foundation (A2016172S).References
1. Tisdall, M. Dylan, Aaron T. Hess, Martin Reuter, Ernesta M. Meintjes, Bruce Fischl, and André JW van der Kouwe. "Volumetric navigators for prospective motion correction and selective reacquisition in neuroanatomical MRI." Magnetic resonance in medicine 68, no. 2 (2012): 389-399.
2. Hess, Aaron T., M. Dylan Tisdall, Ovidiu C. Andronesi, Ernesta M. Meintjes, and André JW van der Kouwe. "Real-time motion and B0 corrected single voxel spectroscopy using volumetric navigators." Magnetic resonance in medicine 66, no. 2 (2011): 314-323.
3. Thesen, Stefan, Oliver Heid, Edgar Mueller, and Lothar R. Schad. "Prospective acquisition correction for head motion with image-based tracking for real-time fMRI." Magnetic Resonance in Medicine 44, no. 3 (2000): 457-465.
4. Lekien, Francois, and J. Marsden. "Tricubic interpolation in three dimensions." International Journal for Numerical Methods in Engineering 63, no. 3 (2005): 455-471.
5. Zhang, Yingzhuo, Iman Aganj, Andre J. van der Kouwe, and M. Dylan Tisdall. "Effects of Resolution and Registration Algorithm on the Accuracy of EPI vNavs for Real Time Head Motion Correction in MRI." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, pp. 143-151. 2016.
6. Jenkinson, Mark. "Measuring transformation error by RMS deviation." Studholme, C., Hill, DLG, Hawkes, DJ (1999).
7.G. Guennebaud, B. Jacob, et al. Eigen v3. http://eigen.tuxfamily.org, 2010.
8. Zhang, Yingzhuo, GitHub repository https://github.com/zyzdiana/MotionCorrection
Figures