Purpose

Since different patient motion sensing strategies have unique advantages and disadvantages, selection of an optimal technique is often task specific. Generally, orientation and translation are estimated with different sensitivities. In marker-based optical motion tracking¹, orientation is encoded using retrograte markers and in active marker-based approaches² through position measurements of rigidly constrained points. In both cases orientation is affected by factors (for example, Moire pattern encoding resolution or the physical distance between active markers) that don’t affect the translation measurements. Navigator approaches are no different as the MR signal behaves differently for changes in orientation than translations. In this work we present a model that can be used to fuse independently acquired orientation and translation estimates. Previously³ we presented a low cost device (VectOrient) that uses a vector-based approach to precisely measure orientation in the MRI scanner independently of the pulse sequence. Here we aim to fuse the high temporal resolution orientation estimates from (VectOrient) with noisier translation estimates obtained using high-speed linear navigators.

Methods

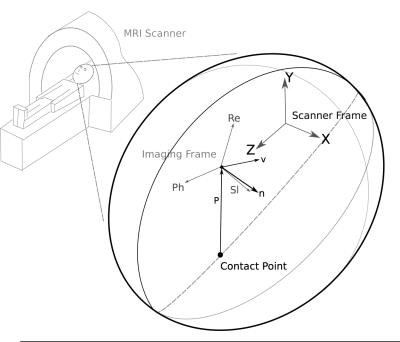
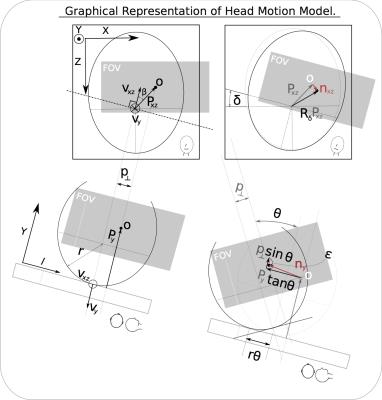
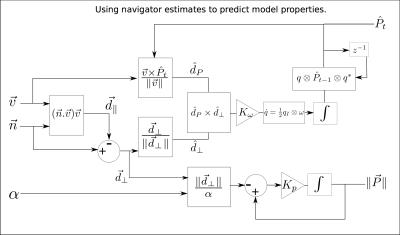
Patient set-up is well defined for MRI brain imaging. The subject is placed head-first-supine into the MRI scanner. The reference frames in Figure 1 are therefore defined for the model description. As neck muscles aren’t effective at lifting the head in this position, it is assumed that the subject’s head remains in contact with the scanner bed. The vector $$$\vec{P}$$$ represents the position of the origin of the field of view with respect to the point at which the patient’s head makes contact with the scanner. Unit vector $$$\vec{v}$$$ is the axis of rotation and $$$\vec{n}$$$ is the translation of the field of view after undergoing the rotation about $$$\vec{v}$$$ by an angle $$$\alpha$$$. Modelling subject head motion as rolling (Figure 2); in much the same way as a ball/sphere rolls over a surface, a relationship between orientation and translation can be established. To simplify co-ordinate transforms, the predicted displacement is written in terms of two orthogonal reference frames aligned to the vertical (Y -axis) and horizontal (parallel to the XZ plane) components of the unit axis of rotation $$$\vec{v}$$$. The rotation $$$\alpha$$$ about $$$\vec{v}$$$ is therefore broken up into two rotations, an angle $$$\delta$$$ about $$$\vec{v}_y$$$ and then an orthogonal rotation of $$$\theta$$$ about $$$\vec{v}_{xz}$$$ as shown in figure 2. The translation of the field of view is:$$\vec{n}=\vec{n}_y+\vec{n}_{xz}$$It follows that,$$\vec{n}_{xz}=R_{\delta}\vec{P}_{xz}-\vec{P}_{xz},$$$$\vec{n}_{xz}=\begin{pmatrix}P_x(\cos\delta-1)+P_z\sin\delta \\ 0 \\ P_z(\cos\delta-1)-P_x\sin\delta \end{pmatrix}$$The translation term on the plane normal to $$$\vec{v}_{xz}$$$:$$\vec{n}_{y}=\big( \vec{l}P_y\tan\theta+\vec{p}_{\perp}\sin\theta\big)+\epsilon (\theta,\vec{p},r),$$where $$$\vec{l} =\frac{\vec{v}_{xz}}{\|\vec{v}_{xz}\|}\times\vec{y}$$$ and $$$\vec{p}_{\perp}=\vec{y}\|\vec{P}_{xz}\|\sin\beta=\vec{P}_{xz}\times\frac{\vec{v}_{xz}}{\|\vec{v}_{xz}\|}$$$ giving,$$\vec{n}_y = \begin{pmatrix} -\frac{v_z}{\|\vec{v}_{xz}\|} P_y \tan \theta \\ \big(v_xP_z-v_z P_x \big) \frac{\sin\theta}{\|\vec{v}_{xz}\|} \\ \frac{v_x}{\|\vec{v}_{xz}\|} P_y \tan\theta \end{pmatrix} + \begin{pmatrix} -\frac{v_z}{\|\vec{v}_{xz}\|} \big( r(\theta-\sin\theta)+p_{\perp}(1-\cos\theta) \big) \\ (r-P_y)(1-\cos\theta) \\ \frac{v_x}{\|\vec{v}_{xz}\|} \big( r(\theta - \sin\theta)+p_{\perp}(1-\cos\theta) \big) \end{pmatrix}$$assuming small angles,$$\vec{n}\approx\begin{pmatrix} P_z\delta-\frac{v_z}{\|\vec{v}_{xz}\|}P_y\theta \\ \frac{\theta}{\|\vec{v}_{xz}\|}\big( v_xP_z-v_zP_x\big ) \\ \frac{v_x}{\|\vec{v}_{xz}\|}P_y\theta-P_x\delta\end{pmatrix}$$ The vertical displacement is defined with the location of the field of view and is subject independent. The horizontal displacement $$$\vec{P}_{xz}$$$, is more difficult to measure although one can assume it remains smaller than $$$P_y$$$ and its effect is scaled by $$$\beta$$$ which is small with symmetrical brain imaging. The model was validated using in vivo scan data where orientation and translation estimates were available. In an example application a filter was developed which fuses navigator translation data and orientation measurements, while observing the vector $$$\vec{P}$$$ (Figure 3). This is achieved by continuously feeding back the navigator and orientation data to rotate and scale $$$\vec{P}$$$ such that the predicted translation follows the navigator. The estimate of $$$\vec{P}$$$ is tracked at a slower rate than the displacement $$$\vec{n}$$$ effectively smoothing noise in the navigator estimates.

Results

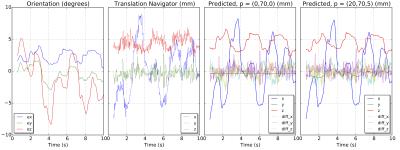
As can be seen from Figure 4, the model explains subject translation even in cases where complex head motion occurs. There is very little difference between the outputs showing the assumption of no slipping remains valid. Figure 5, shows the ability of the observer to track the contact point using the model when orientation and translation data is available. The synthesised translation output is much smoother as the time response for tracking the properties of $$$\vec{P}$$$ using the navigator data can be adjusted with $$$K_p$$$ and $$$K_{\omega}$$$(Figure 3). It is important to note that filter translation output still has the quick response of the orientation estimates.

Discussion

The robustness to subject variance shows that this model could prove useful when noise in orientation and translation data are complementary in nature. Another application is the fusion of low temporal resolution estimates (vNav⁴) with faster sequence independent approaches.

Conclusion

Patient orientation and translation are very strongly correlated. Further constraints do exist and methods of fully quantifying subject motion using very few sensors may be possible.