3942
Radial MRI and model-based iterative reconstruction for motion robust quantification of the water content in the brain at 3 Tesla1Institute of Neuroscience and Medicine – 4, Medical Imaging Physics, Forschungszentrum Juelich GmbH, Juelich, Germany, 2Department of Neurology, Faculty of Medicine, RWTH Aachen University, JARA, Aachen, Germany
Synopsis
Quantitative water content mapping is a promising technique to monitor brain diseases. However, established protocols suffer from long acquisition times and sensitivity to patient motion. To overcome these issues, we propose to use golden angle radial MRI and model-based iterative reconstruction. This allows accurate and precise estimation of water content and T1 values, while providing significantly higher motion robustness, as shown in phantom and in vivo experiments. The golden angle-based k-space sampling allows for a nearly optimal k-space coverage even in the event of early termination of measurement. This opens the opportunity to apply such a technique in the clinic.
Purpose
Quantitative, non-invasive estimation of tissue water content using MRI is a promising technique to monitor and interpret brain diseases. Highly precise and robust mapping of the water content and its distribution requires a significant number of corrections. A well established approach to it is implemented in a number of cohorts1,2,3, which allows one to estimate the water content and relaxation times (T1, T2*) simultaneously. However, longer acquisition times and sensitivity to patient motion have impeded its widespread clinical application. Following the work of Block et al.4, we investigated the combination of radial MRI and model-based iterative reconstruction to improve motion robustness, while preserving accuracy and precision.Materials and Methods
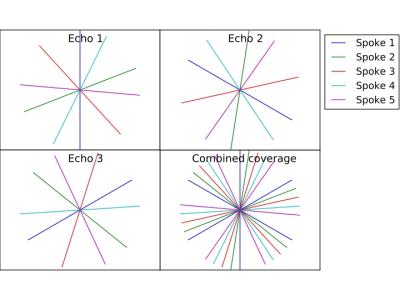
MR acquisitions were performed using a multi-echo gradient echo sequence with the golden angle ordering scheme5. To further improve k-space coverage, inter-echo rotations were performed, rotating consecutive k-spaces by 180°/number of echoes (Figure 1). Model-based iterative reconstruction was performed according to Block et al.4, extending the parameters to the complex plane by including the field map and the initial phase. Prior to reconstruction, the data were compressed to 8 virtual channels via singular value decomposition to reduce reconstruction time. A gradient delay correction was performed following Block et al.6 ESPIRiT7 was used to estimate coil sensitivities from the first echo.
Quantitative MR imaging methods were validated using a “revolver” phantom, containing nine probes with various H2O/D2O concentrations, doped with gadolinium to alter T1 and T2* properties. Measurements were performed on a 3T scanner (MAGNETOM Trio, INM-4 Jülich, Germany) using a 12-element head coil and 2D multi-echo gradient echo sequences (TR=(520ms, 1800ms), TE1=5ms, ΔTE=5ms, FA=(90°/40°), (2/10) echoes, 1x1x2mm3 resolution, 256x256 matrix size, 32 slices, BW=720Hz/px, slice gap=2mm, 256 spokes, base resolution 256)2,3. Additional scans were acquired to compensate for transmit and receive field non-uniformities, following Abbas et al.3
After obtaining prior written informed consent from healthy volunteers, fully sampled whole-brain data sets were measured with the same protocol using a 32-element head coil. In addition to the radial acquisitions, Cartesian acquisitions with the same field-of-view and parameters were acquired. The total scan time was 22 minutes, with 10 minutes for the radial and Cartesian acquisitions, respectively, and 2 minutes for the correction scans. Reconstruction and post-processing were performed with in-house software written in MATLAB and Python.
Results and Discussion
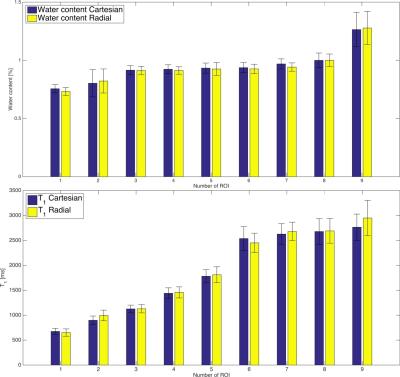
The phantom water content and T1 values obtained with the radial acquisition are in good agreement with the Cartesian acquisition (Figure 2).
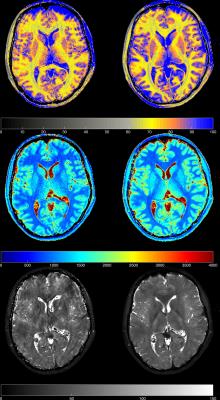
A comparison of in vivo water content, T1 and T2* maps estimated using the Cartesian and radial acquisitions is shown in Figure 3. White matter and grey matter water content and T1 values are in agreement with literature values1,2,3. Joint histogram analysis from a representative volunteer is shown in Figure 4, where voxel-wise values are plotted from Cartesian and radial water content and T1 maps. The volunteer was instructed to deliberately move slightly during both measurements. The quantitative maps from the Cartesian acquisitions suffered from motion artefacts, whereas the ones from radial acquisition were not significantly affected (Figure 3). This verifies our hypothesis of using radial MRI for estimation of water content in the presence of patient motion
The observed motion robustness of radial sequences compared to Cartesian sequences has two reasons. First, motion translates into k-space modulation, which is negligible within short sampling intervals, e.g. along the readout direction. However, in Cartesian sampling, signal modulation also appears along the phase encoding direction, which leads to ghosting artefacts, as shown in Figure 3. Since radial sequences lack a phase encoding direction, they are not affected by this modulation. Additionally, k-space centre oversampling leads to an averaging effect that compensates for errors in single spokes.8
Conclusion
This is the first in vivo study demonstrating the feasibility to estimate quantitative water content using a radial acquisition technique. The novelty of the radial acquisition-based water content mapping lies in motion robustness, whereas in line with the literature values, accurate and precise quantification was achieved. This ambitious technique opens the opportunity to employ quantitative mapping in a clinical setting routinely, whereas, in comparison, Cartesian acquisition techniques are marred by motion artefacts. The golden angle ordering provides nearly optimal k-space coverage even in the event of early termination of the measurement.Acknowledgements
No acknowledgement found.References
1. Neeb H, Zilles K, Shah NJ. A new method for fast quantitative mapping of absolute water content in vivo. Neuroimage. 2006;31(3):1156-68.
2. Neeb H, Ermer V, Stocker T, Shah NJ. Fast quantitative mapping of absolute water content with full brain coverage. Neuroimage. 2008;42(3):1094-109.
3. Abbas Z, Gras V, Mollenhoff K, Keil F, Oros-Peusquens AM, Shah NJ . Analysis of proton-density bias corrections based on T1 measurements for robust quantification of water content in the brain at 3 Tesla. Magnetic Resonance in Medicine. 2014;72(6):1735-1745.
4. Block KT, Uecker M, Frahm J. Model-based iterative reconstruction for radial fast spin-echo MRI. IEEE Trans Med Imaging. 2009;28(11):1759-1769.
5. Winkelmann S, Schaeffter T et al. An Optimal Radial Profile Order Based on the Golden Ratio for Time-Resolved MRI. IEEE Transactions on medical imaging. 2007;26(1):68-76.
6. Block KT, Uecker M. Simple Method for Adaptive Gradient-Delay Compensation in Radial MRI. In Proceedings of the 19th Annual Meeting of ISMRM, Montreal, Canada. 2011;():2816.
7. Uecker M, Lai P et al. ESPIRiT - an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magnetic Resonance in Medicine. 2014;71(3):990-1001.
8. Block KT. Advanced methods for radial data sampling in magnetic resonance imaging. SUB University of Goettingen. 2008.
Figures