Synopsis

We propose a non-parametric method of jointly estimating non-rigid motion and the underlying image without the assumption of motion smoothness. We model non-rigid motion as local linear translation, which is equivalent to convolution with 1-sparse kernels. We then pose the non-rigid motion recovery problem as a sparse blind deconvolution problem. Our reconstruction results demonstrate that non-rigid motion can be well approximated as local translation motion using the proposed method. The proposed formulation can also be viewed as a generalization of locally low rank reconstruction.

Purpose

Dynamic MRI is inherently under-sampled and requires the incorporation of prior models for high spatial-temporal resolution image reconstruction. Low rank methods^1-5 are effective in capturing MR dynamics, including contrast enhancement, cardiac perfusion and parameter mapping, yet large motion still poses problems. Various methods^6-12 were proposed to incorporate motion estimation with iterative image reconstruction, yet often involve image registration or optical flow models that assume smoothness of the motion field. This assumption can lead to erroneous motion estimation when motion is not smooth.

In this work, we propose a non-parametric method of jointly estimating non-rigid motion and the underlying image without the assumption of motion smoothness. We model non-rigid motion as local linear translation, which is equivalent to convolution with 1-sparse kernels. We then pose the non-rigid motion recovery problem as a sparse blind deconvolution problem. The proposed method inherits the effectiveness of sparse methods and can also be viewed as a generalization of locally low rank reconstruction, which is robust to intensity variation.

Theory

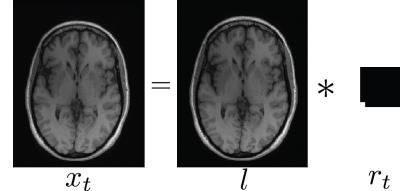
To illustrate our proposed method, we first focus on the global linear translational model. Under this model, the image $$$x_t$$$ at time $$$t$$$ is a shifted version of an underlying image $$$l$$$, which can be represented as convolution with a 1-sparse motion kernel $$$r_t$$$, that is,

$$x_t = l \ast r_t$$

The location of the non-zero element in the 1-sparse kernel represents the amount of linear translation at time $$$t$$$. The size of the motion kernels determines the maximum linear translation possible, which is limited by physical constraints. Hence, recovering the sparse motion kernel allows us to extract motion information, without the assumption of motion smoothness. Figure 1 illustrates the global translational model.

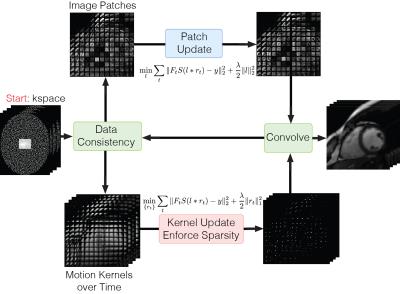
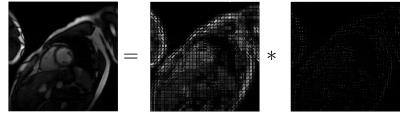
To extend to non-rigid motion, we adopt the local translation approximation¹³ and model each local patch motion as local translation over time. Figure 2 shows the proposed decomposition applied on a reconstructed cardiac dataset with overlapping patches of size 16x16 with local motion kernels of size 16x16. Under the above motion model, the problem of recovering non-rigid motion becomes equivalent to recovering the local sparse motion kernels. Hence, we consider the following objective function for joint estimation of non-rigid motion and image:

$$f(l, r_t)=\sum_t \frac{1}{2}\|F_tS(l\ast r_t)-y_t\|_2^2+\frac{\lambda}{2}(\|l\|_2^2+\|r_t\|_1^2)$$

where $$$F_t$$$ is the Fourier sampling operator at time $$$t$$$, $$$S$$$ is the sensitivity operator, $$$y_t$$$ is the acquired k-space data at time $$$t$$$, $$$\lambda$$$ is the regularization parameter and $$$\ast$$$ denotes the local convolution operator. Alternating minimization can be used to reduce the objective function, with each subproblem being convex. (Figure 3)

We enforce sparsity within each motion kernel $$$r_t$$$ via a mixed $$$\ell 1$$$ norm within the kernel and $$$\ell 2$$$ norm across time, also known as the Elitist LASSO¹⁴. The $$$\ell 2$$$ norm is essential because it ensures that each motion kernel has at least one non-zero element¹⁴. The $$$\ell 1$$$ also leads to a more robust motion estimation because continuous motion can be represented as general sparse kernels instead of 1-sparse. Finally, the proposed formulation can be viewed as a generalization of locally low rank reconstruction¹⁵. In particular, when the motion kernel size is 1, the proposed formulation is equivalent to constraining the local patches to be of rank-1.

Results

We applied our proposed method on a cardiac cine dataset obtained from the L+S code repository⁴. The data was acquired with a Turbo-FLASH on a 3T Siemens Trio scanner. The dataset has a matrix size of 256x256 with 24 time frames and 8 coils and was retrospectively under-sampled by a factor of 8.

Figure 4 shows the reconstructed result with overlapping patches of size 16x16 with local motion kernels of size 16x16, 30 outer iterations and with 30 inner iterations for each subproblem using FISTA¹⁶. Undersampling artifacts were mostly resolved in the reconstructed images and motion kernels were also recovered. Visually, the non-zero element location corresponds to the amount of local translation.

We also show that the proposed method can potentially be used on low spatial resolution image navigators to reliably extract motion information. Figure 5 shows the reconstructed result on the 32x32 low frequency kspace region with overlapping patches of size 4x4 with local motion kernels of size 4x4.

Discussion

Acknowledgements

References

[1] Z. P. Liang, “Spatiotemporal imaging with partially separable functions,” in Proc. IEEE Int. Symp. Biomed. Imag.: From Nano Macro, 2007, pp. 988–991.

[2] H. Pedersen, S. Kozerke, S. Ringgaard, K. Nehrke, and W. Y. Kim, “k-t PCA: Temporally constrained k-t BLAST reconstruction using principal component analysis,” Magn. Reson. Med., vol. 62, no. 3, pp. 706–716, Sep. 2009.

[3] Trzasko J, Manduca A, Borisch E. Local versus Global Low-rank Promotion in Dynamic MRI Series Reconstruction. Proc Int Symp Magn Reson in Medicine 2011; p. 4371.

[4] R. Otazo, E. Candes, and D. K. Sodickson, “Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of back- ground and dynamic components.” Magn. Reson. Med., vol. 73, no. 3, pp. 1125–1136, Mar. 2015.

[5] F. Ong and M. Lustig, “Beyond Low Rank + Sparse: Multiscale Low Rank Matrix Decomposition,” IEEE J. Sel. Top. Signal Process., vol. 10, no. 4, pp. 672–687, Jun. 2016.

[6] Batchelor PG, Atkinson D, Irarrazaval P, Hill DLG, Hajnal J, Larkman D. Matrix description of general motion correction applied to multishot images. Magnetic Resonance in Medicine 2005; 54:1273–1280.

[7] Odille F, Vuissoz PA, Marie PY, Felblinger J. Generalized reconstruction by inversion of coupled systems (grics) applied to free-breathing mri. Magnetic Resonance in Medicine 2008; 60:146–157.

[8] Cruz G, Atkinson D, Buerger C, Schaeffter T, Prieto C. Accelerated motion corrected three- dimensional abdominal mri using total variation regularized sense reconstruction. Magnetic Resonance in Medicine 2016; 75:1484–1498.

[9] High spatial and temporal resolution cardiac cine mri from retrospective reconstruction of data acquired in real time using motion correction and resorting. Magnetic Resonance in Medicine 2009; 62:1557– 1564.

[10] Xue H, Ding Y, Guetter C, Jolly MP, Guehring J, Zuehlsdorff S, Simonetti OP. Motion compensated magnetic resonance reconstruction using inverse-consistent deformable registration: Application to real-time cine imaging. Medical image computing and computer-assisted intervention 2011; 14:564–572.

[11] Asif MS, Hamilton L, Brummer M, Romberg J. Motion-adaptive spatio-temporal regularization for accelerated dynamic mri. Magnetic Resonance in Medicine 2013; 70:800–812.

[12] R. Otazo, T. Koesters, and E. Candes, “Motion-guided low-rank plus sparse (L+ S) reconstruction for free-breathing dynamic MRI,” presented at the Proceedings of ISMRM, 2014.

[13] Cheng JY, Alley MT, Cunningham CH, Vasanawala SS, Pauly JM, Lustig M. Nonrigid motion correction in 3d using autofocusing with localized linear translations. Magnetic Resonance in Medicine 2012; 68:1785–1797.

[14] M. Kowalski, “Sparse regression using mixed norms,” Applied and Computational Harmonic Analysis, 2009.

[15] J. Trzasko, A. Manduca, and E. Borisch, “Local versus global low-rank promotion in dynamic MRI series reconstruction,” ISMRM, 2011.

[16] A. Beck and M. Teboulle, “A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems,” SIAM J. Imaging Sci., vol. 2, no. 1, pp. 183–202, Jan. 2009.