Purpose

Motion-compensated diffusion-prepared (dprep) sequences have been emerging as an alternative for high resolution and low distortion diffusion imaging especially in body applications^1-4. In dprep sequences, phase errors induced by motion and eddy currents during the diffusion encoding period affect not only the magnitude but also the phase of the acquired signal⁵. With motion-compensated diffusion preparation, the effect of motion-induced phase errors is minimized but that of eddy-current-induced phase errors remains. In the present study, we investigate the performance of the use of phase cycling and the use of magnitude stabilizers in compensating for the eddy current effects in a motion-compensated dprep-TSE sequence.

Theory

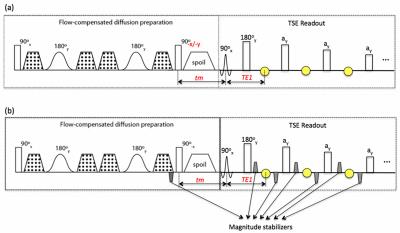
Fig. 1a shows the sequence diagram for a flow-compensated dprep-TSE sequence. The transverse magnetization at the tip-up pulse, $$$M_{xy}(90_{-x}-)$$$, in the presence of a phase error $$$\phi_{voxel}$$$ induced by the diffusion encoding period, becomes, $$M_{xy}(90_{-x}-) = M_{prep}e^{j\pi/2}e^{j\phi_{voxel}},\ (1)$$ where $$$M_{prep}$$$ is the magnitude of the diffusion-prepared magnetization. After the tip-up RF pulse along the –x direction and the T1 relaxation during the time tm (Fig. 1), the longitudinal magnetization right before the TSE readout excitation is $$M_z(90_{+x}-) = M_{prep}cos\phi_{voxel}e^{-tm/T1} + M_0(1 – e^{-tm/T1}). \ (2)$$ When the tip-up RF pulse is along the –y direction, Equation (2) becomes $$M_z(90_{+x}-) = M_{prep}sin\phi_{voxel}e^{-tm/T1} + M_0(1-e^{-tm/T1}). \ (3)$$ Equations (2) and (3) reveal a signal magnitude modulation dependent on the phase error. When eddy currents are the major cause of $$$\phi_{voxel}$$$, it has been proposed that the magnitude modulation can be eliminated by phase cycling of the tip-up RF pulse between –x and –y (i.e., 90^o out of phase) and taking the sum-of-squares (SOS) of the resulted signals⁶. From Equations (2) and (3), it can be seen that the phase cycling method only works if the T1 relaxation effect is negligible, which may not be true when $$$M_{prep}$$$ is small (high b-value encoding, high diffusivity) or tm is significant. Magnitude stabilizers are gradients (grey trapezoids in Fig. 1b) that are added to the dprep-TSE sequence for minimizing magnitude modulation due to phase errors without the need of phase cyling⁷. In the presence of the magnitude stabilizers, the magnetization at the first echo in the TSE readout (first yellow circle in Fig. 1b) can be expressed as $${M_{xy}}^1=\frac{1}{2}M_{prep}e^{-tm/T1}e^{-TE1/T2}e^{j(\phi_{voxel}+\pi/2)}, \ (4)$$ which has the magnitude independent of the phase error but at a cost of 50% signal loss.

Methods

Phantom (water) and in-vivo experiments (human calf muscle) were performed to compare the performance of the phase cycling method and the use of magnitude stabilizers (Fig. 1) on a 3 T Philips system (Philips Ingenia, Best, the Netherlands) using a tranamit/receive 16-channel knee coil. Ten diffusion encoding directions were acquired at a b-value of 400 s/mm2 with TE/TR=60/1700 ms, tm=11 ms, TSE factor=60, voxel size=2.5x2.5x4 mm³ (phantom) and 1.5 x1.5x6 mm³ (in-vivo calf muscle). Fat suppression was performed with SPAIR. In the phase cycling method (Fig. 1a), two repetitions with the tip-up RF pulse along –x and –y were acquired.

Results

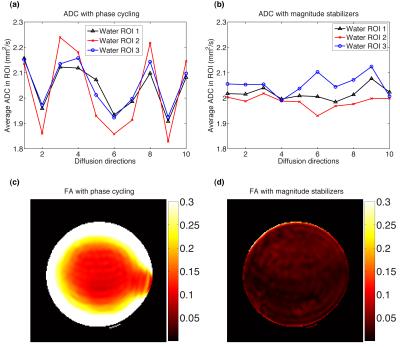
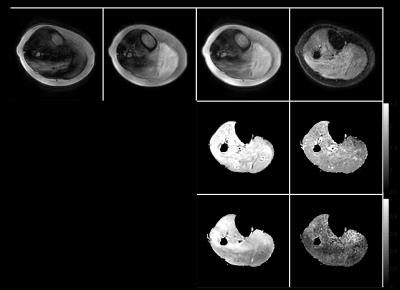
The “tip-up -x” and “tip-up -y” diffusion signal curves across directions exhibited the expected opposite signal variation (Fig. 2a). The “SOS” curve still showed significant oscillation across diffusion directions (Fig. 2b) and the instability of diffusion-weighted magnitude led to a fluctuation in the estimated ADC per direction (Fig. 3a) and an erroneously high FA (Fig. 3c). Magnitude stabilizers gave more stable signal across diffusion directions (Fig. 2c) and resulted in lower variation in estimated ADC per direction (Fig. 3b) and low FA values (<0.05). In vivo calf diffusion-weighted images showed a spatial magnitude modulation in “tip-up -x” and “tip-up -y” images (Fig. 4). The “SOS” image only showed partial magnitude modulation reduction while the image acquired with magnitude stabilizers exhibited no magnitude modulation. More reasonable mean ADC (ROI average of 1.6x10^-3 mm²/s) and FA (ROI average of 0.3) values were achieved with magnitude stabilizers where as the phase cycling method overestimated mean ADC and FA maps.

Discussion and conclusion

Phase cycling of the tip-up RF pulse and taking the SOS of the resulted signals shows insufficient performance in removing the signal magnitude modulation caused by eddy-current-induced phase errors. It is presently shown that the phase cycling method failed even in a water phantom with a long T1. The performance of the phase cycling method is expected to be worse in tissues/substances with shorter T1 value. Therefore, magnitud stabilizers should be the method of choice for compensating eddy-current-induced phase errors in motion-compensated dprep-TSE sequences even at the cost of 50% in signal.

Acknowledgements

The present work was partially supported by Philips Healthcare.