3918

Robust Accelerated Reconstruction for Bloch-Siegert B1-mapping
Andreas Lesch1, Matthias Schlögl1, and Rudolf Stollberger1,2

1Institute of Medical Engineering, Graz University of Technology, Graz, Austria, 2BioTechMed Graz, Graz, Austria

Synopsis

In this work we evaluate the performance and the robustness of an algorithm for the reconstruction of B1+-maps out of highly accelerated Bloch-Siegert data. The algorithm is based on variational modeling with a problem specific regularization approach. We evaluate the influence of different sampling patterns on the achievable accuracy and sampling efficiency and the influence of both regularization parameters on the final result. All results are compared to the fully-sampled reference using conventional reconstruction. We can show the general robustness of our algorithm and the most effective sampling pattern for this purpose.

Introduction

For many applications in MRI a fast and accurate B$$$_{1+}$$$-measure is an important prerequisite at high and ultrahigh field-strengths. The method of Bloch-Siegert (BS) was shown to be accurate and robust against many influences.1 Due to the independence of T1, low repetition-times (TR) are possible, leading to fast 2D-acquisitions. Nevertheless, the method suffers from high specific-absorption-rates (SAR) which limit the minimum possible TR, leading to prolonged acquisition-times in 3D. In2 we presented an algorithm based on variational-modeling, which is able to reduce the necessary amount of data significantly, with only minor reduction in accuracy.2 However, its final applicability depends strongly upon choosing suitable sampling-strategies and robust reconstruction parameters - an issue that is concludingly addressed in this work.

Methods

The algorithm, described in,2 consists of a two-step procedure, where in the first step a TGV-regularization term3,4 is applied to reconstruct magnitude and phase of the underlying image. In the second step a H1-regularization term is applied to enforce spatial smoothness of the underlying B1+-field. For further details we refer to.2

$$\hat{u}=\arg\min_u\frac{\lambda}{2}\parallel\,k_+-\mathcal{F}\left(u\right)\,\parallel_2^2+TGV\left(u\right)$$

$$\hat{v}=\arg\min_v\frac{\mu}{2}\parallel\,k_--\mathcal{F}\left(\hat{u}\,\cdot\,v\right)\,\parallel_2^2+\parallel\nabla\,v\parallel_2^2=e^{-j2\phi_{BS}}$$

The evaluation was performed on a 3D-dataset acquired at 3T (Skyra, Siemens, Erlangen Germany) in the brain of a healthy volunteer using a GRE-sequence with the following acquisition parameters: FOV=230$$$^2$$$x64mm, matrix-size=128$$$^2$$$, TR=95ms, TE=13.5ms, $$$\alpha=25°$$$ and a Gaussian BS-pulse with a pulse-constant of $$$K_{BS}=53.4rad/G^2$$$ and an onresonant flip-angle of $$$\alpha_{BS}=1000°$$$.

All achieved results are validated against the B$$$_{1+}$$$-map from the fully-sampled dataset denoted as reference. Each result is further characterized by its mean $$$\Delta_{mean}$$$ and maximum absolute difference $$$\Delta_{max}$$$ to the reference inside a region of interest (ROI), covering the whole brain excluding border regions.

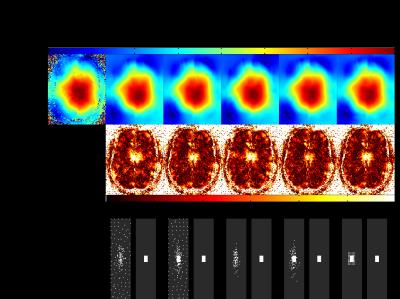
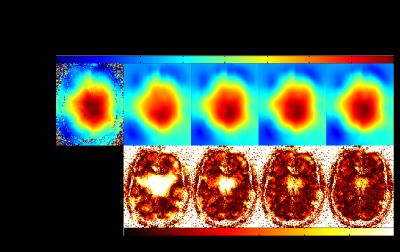
To evaluate the influence of the sampling pattern on the reconstruction result, we first increased the high frequency information in the TGV part, using variable density patterns, as described in5 and with Gaussian density function, where a constant rectangular region in the k-space center with size 10x6 was sampled for the H1-part. Second, we used a rectangular sampling of the k-space center in both datasets with different sizes to account for differnt amounts of sampling in the phase encoding dimensions.

To evaluate the robustness against variations in both regularization parameter, we show the same error measure for a wide range of regularization parameters $$$\mu$$$ and $$$\lambda$$$ for three different acceleration-factors, using a squared sampling patter in k-space center (6x6, 10x10 and 24x24 lines).

Results

In Fig.1 the achieved results and the absolute difference to the fully-sampled reference for different sampling patterns, increasing the high frequency information in the TGV part, are displayed. In Fig.2 and 3 the equivalent results are shown for a rectangular and the initially proposed squared sampling pattern in the k-space center, respectively. Tab.1 shows the mean $$$\Delta_{mean}$$$, maximum $$$\Delta_{max}$$$ absolute difference to the reference measure in percent as well as the achieved effective acceleration $$$R_{eff}$$$ for all shown results. Fig.4 shows the reconstruction error in dependence of both regularization parameters for different accelerations.

Discussion and Conclusion

By using the originally proposed sampling-strategy2 the TGV-reconstruction suffers from missing details, because of the lacking high frequency information and it is not able to account for different dimensions in both phase-encoding directions. The results in Fig.1 and Tab.1 indicate that an additionally sampling of higher frequency information in the TGV-part only leads to a slight improvement compared to a 10x6 rectangular sampling; however the TGV-result itself is improved significantly in all 5 cases. Furthermore, in cases without fully-sampled center the error in the final B$$$_{1+}$$$-map is evenly increased, while decreasing the achievable acceleration $$$R_{eff}$$$ in all cases. The impact of sampling additionally high frequency information in the TGV-reconstruction part is very low on the accuracy of the final B$$$_{1+}$$$-map.

Comparing the results in Fig.2,3 and Tab.1 for the 12x4 rectangular pattern with the initially proposed 8x8 squared pattern, the effective acceleration is increased from $$$R_{eff}=64$$$ to $$$R_{eff}=85$$$, while $$$\Delta_{mean}$$$ and $$$\Delta_{max}$$$ can be reduced from 0.71% to 0.66% and from 5.46% to 4.42% respectively. Compared to the result of the pattern-size 10x10 $$$\Delta_{mean}$$$ lies in the same range and $$$\Delta_{max}$$$ is reduced from 5.1% to 4.4% while doubling the acceleration.

Fig.4 indicates the robustness against variation of both regularization parameters, since errors remain stable over one decade from the optimum.

In general we can conclude the algorithm is very robust against variations in the regularization parameters and different subsampling patterns, if sufficient data-points are acquired in the k-space center. The best sampling efficiency can be reached if a rectangular region in the k-space center is acquired in both reconstruction steps depending on the dimension in phase encoding directions.

Acknowledgements

This work was funded by the Austrian Science Fund (FWF) "SFB 3209-18" and NVIDIA Corporation Hardware grant support

References

1. L. I. Sacolick, F. Wiesinger, I. Hancu, and M. W. Vogel. B1 mapping by bloch-siegert shift. Magn Reson Med, 63(5):1315–1322, May 2010.

2. A. Lesch, M. Schlögl, M. Holler, and R. Stollberger. Highly accelerated Bloch-Siegert B1+ mapping using variational modeling. Proc. ISMRM 24:1875, 2016.

3. F. Knoll, K. Bredies, T. Pock, and R. Stollberger. Second order total generalized variation(tgv) for mri. Magn Reson Med, 65(2):480–491, Feb 2011

4. K. Bredies, K. Kunisch, and T. Pock. Total generalized variation. SIAM Journal on ImagingSciences, 3(3):492–526, 2010

5. F. Knoll, C. Clason, C. Diwoky, and R. Stollberger. Adapted random sampling patterns for accelerated MRI. Magnetic resonance materials in physics, biology and medicine 24.1 (2011): 43-50.

Figures

Fig.1: Achieved B$$$_{1+}$$$-maps including the fully-sampled reference and the reconstruction results for different sampling-patterns in the TGV-part to increase high frequency information and a 10x6 rectangular sampling in the k-space center for the H1-part. The B$$$_{1+}$$$-maps are normalized to the nominal flip-angle of the BS-pulse. Furthermore, the absolute difference to the reference is shown in percent as well as the sampling-pattern for the TGV and H1-part.

Fig.2: Achieved B$$$_{1+}$$$-maps including the fully-sampled reference and the reconstruction results for a rectangular sampling in the k-space center in both reconstruction steps with different sizes. The B$$$_{1+}$$$-maps are normalized to the nominal flip-angle of the BS-pulse. Furthermore, the absolute difference to the reference is shown in percent.

Fig.3: Achieved B$$$_{1+}$$$-maps including the fully-sampled reference and the reconstruction results for the originally proposed squared sampling in the k-space center in both reconstruction steps with different sizes. The B$$$_{1+}$$$-maps are normalized to the nominal flip-angle of the BS-pulse. Furthermore, the absolute difference to the reference is shown in percent.

Fig.4: The mean absolute difference to the fully-sampled reference inside a ROI covering the whole brain excluding border regions is plotted for different values of both regularization parameters $$$\mu$$$ and $$$\lambda$$$ for different acceleration-factors using a squared sampling region in the k-space center.

Tab.1: Mean absolute difference $$$\Lambda_{mean}$$$ and maximum absolute difference $$$\Lambda_{max}$$$ to the fully-sampled reference are given for all evaluated sampling patters as well as the achieved acceleration factor $$$R_{eff}$$$.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3918