3917

Interaction between trajectory deviations and B0 field inhomogeneity in readout-segmented EPI and spiral imaging

Yoko A Spirig^1,2, Nadine N Graedel², Lars Kasper¹, Karla L Miller², Robert Frost², Stuart Clare², Klaas P Pruessmann¹, and S Johanna Vannesjo²

¹Institute for Biomedical Engineering, University of Zurich and ETH Zurich, Zurich, Switzerland, ²FMRIB centre, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom

Synopsis

We studied the effect of encoding imperfections due to gradient errors with a focus on their interaction with $$$B_0$$$ inhomogeneities. Using a simulation framework, we retrospectively sampled data using k-space trajectories of two fast imaging sequences and compared reconstructions based on nominal, gradient impulse response (GIRF) predicted and measured (ground-truth) trajectories for spiral and readout-segmented EPI sequences. We found that the detrimental impact of trajectory imperfections on image quality is strongly amplified by $$$B_0$$$ inhomogeneities, especially for non-Cartesian trajectories. Furthermore, we confirmed that GIRF-predicted trajectory based reconstructions (requiring only a one-time calibration) allow effective artifact reduction.

Purpose

To better understand the impact of gradient imperfections and their interaction with $$$B_0$$$ field inhomogeneities on reconstructions using a full encoding model.

Introduction

Fast acquisition strategies, especially those using non-Cartesian sampling, have been notoriously difficult to implement successfully, mainly due to two challenges: Firstly the actual gradient waveforms often differ significantly from prescribed shapes and secondly $$$B_0$$$ inhomogeneity interacts with the spatial encoding, leading to severe image artifacts. This can be tackled by using a full encoding model that takes both gradient imperfections and $$$B_0$$$ offsets into account, as recently demonstrated for single-shot spiral imaging¹. In measured MRI data both gradient and $$$B_0$$$ encoding imperfections are present to varying degrees. To isolate the effect of gradient imperfections and their interactions with $$$B_0$$$ field imperfections we use a simulation framework. We investigate the impact on image artifacts for spiral sampling and readout-segmented EPI (RS-EPI) and we further test the feasibility of using a measured gradient impulse response function (GIRF) to model the gradient system for these types of sequences^2-4.

Methods

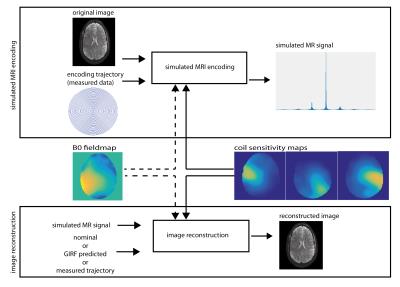
Gradient field measurements were performed on a 7 T Siemens system using a dynamic field camera (Skope)⁵. Field responses to a spiral (maximal gradient amplitude 31 mT/m, 1.1 mm in-plane resolution, undersampling factor of 3) and a RS-EPI⁶ (7 segments, 1.2 mm in-plane resolution, 0.32 ms echo-spacing, readout gradient amplitude scaling factor of 1.022) trajectory were acquired. The system GIRF was determined as described in Ref 3. Directly measured trajectories were used to simulate the MR signal $$$s(t)$$$ from a previously acquired brain image $$$m(\mathbf{r})$$$ (Fig. 1), using the following discrete signal model:

$$s_\kappa(t)={\sum_i} c_\kappa(\mathbf{r}_i)\cdot m(\mathbf{r}_i)\cdot \exp(-ik(t)\cdot \mathbf{r}_i+ \gamma \cdot \Delta B_0(\mathbf{r}_i)\cdot t)$$

where k denotes the trajectory, c the coil sensitivity of coil $$$\kappa$$$ and i counts the voxels. The encoding was performed i) assuming a perfectly homogeneous background field, and ii) introducing a $$$B_0$$$ fieldmap, obtained from the same subject as the encoded image at 7 T. In all reconstructions, measured coil sensitivity maps (16ch coil) were used in the encoding. Simulated MR images were reconstructed using nominal, GIRF-predicted and measured trajectories. The nominal and GIRF-predicted trajectories were time-matched to the measured trajectory to eliminate artifacts due to a simple delay. Image reconstruction was performed by inversion of the signal model equation, using a gridding-based iterative CG solver^7,8. In the cases including a simulated $$$B_0$$$ field offset, the encoding effect of the field offset was incorporated using multi-frequency interpolation⁹. Reconstruction results were evaluated using the root-mean-square error (RMSE) to the ground-truth image.

Results

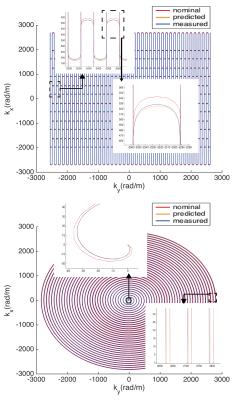
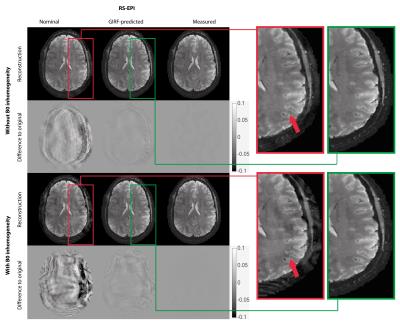
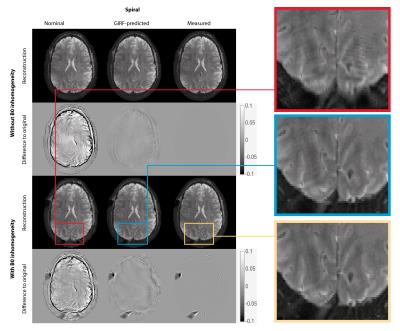
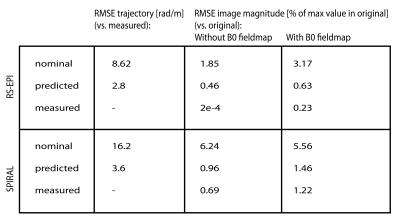
GIRF-prediction yielded trajectories that closely matched measured trajectories for both the RS-EPI and the spiral sequence (Fig. 2). Compared to nominal trajectories, GIRF-prediction reduced the RMSE by a factor of 3 for the RS-EPI and 4.5 for the spiral sequence (Tab. 1). In the absence of background field inhomogeneity images based on nominal trajectories exhibited only minor artifacts: subtle ghosting for RS-EPI, geometric compression for spiral (Figs. 3/4, top left). Artifact levels increased considerably in the presence of $$$B_0$$$ inhomogeneity (Figs. 3/4, bottom left). For the RS-EPI, signal intensity modulations over the image appeared and the ghosting artifact intensified. In the spiral sequence, the $$$B_0$$$ field caused blurring and ringing artifacts. The GIRF-predicted images yielded substantially improved image quality for both types of sequences and both without/with $$$B_0$$$ inhomogeneity (RMSE reduced by factors 3.8 to 6.5 compared to nominal trajectories), with only very small differences to the reconstructions using the measured trajectory (Figs. 3/4, middle/right, Table 1). Residual RMSE in the case of measured trajectories is due to incomplete sampling in the case of spiral trajectories or $$$B_0$$$ field offsets, combined with finite accuracy of the numerical implementation of the reconstruction.

Discussion and Conclusion

The results presented here indicate that uncorrected trajectory deviations lead to more severe image artifacts in the presence of $$$B_0$$$ field inhomogeneity, despite perfect knowledge of the encoding $$$B_0$$$ fieldmap. This is intuitively understandable, considering that the $$$B_0$$$ correction relies on accurate geometric congruency between the $$$B_0$$$ fieldmap and the encoded image. We conclude that accurate knowledge of acquired k-space locations is even more important in situations where B0 field offsets affect the encoding. For the trajectories investigated in this work, a GIRF model yielded sufficient accuracy to achieve good reconstructions both without and with $$$B_0$$$ field inhomogeneity. The simulation framework used here provides full control over the encoding model, which is never given under real-world conditions. In a future study, interactions between gradient imperfections and other types of encoding disturbances could be investigated, as well as the sensitivity to imperfect knowledge of the latter.

Acknowledgements

This project has received funding from the Oxford-Brain@McGill-ZNZ Partnership in the Neurosciences (Ref. OMZPN/2015/1/3) and from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 659263. Technical support from Andrew Dewdney at Siemens Healthcare is gratefully acknowledged.

References

1. Betram J. Wilm, Christoph Barmet, Simon Gross, Lars Kasper, S. Johanna Vannesjo, Max Haeberlin, Benjamin E. Dietrich, David O. Brunner, Thomas Schmid, and Klaas P. Pruessmann. Single-Shot Spiral Imaging Enabled by an Expanded Encoding Model: Demonstration in Diffusion MRI. Magnetic Resonance in Medicine, 2016, In Press.

2. Nii Okai Addy, Holden H. Wu, and Dwight G. Nishimura. Simple method for MR gradient system characterization and k-space trajectory estimation. Magnetic Resonance in Medicine, 2012, 68:120-129

3. S. Johanna Vannesjo, Maximilian Haeberlin, Lars Kasper, Matteo Pavan, Bertram J. Wilm, Christoph Barmet, and Klaas P. Pruessmann. Gradient system characterization by impulse response measurements with a dynamic field camera. Magnetic Resonance in Medicine, 2013, 69:583-593

4. S. Johanna Vannesjo, Nadine N. Graedel, Lars Kasper, Simon Gross, Julia Busch, Maximilian Haeberlin, Christoph Barmet, and Klaas P. Pruessmann. Image Reconstruction Using a Gradient Impulse Response Model for Trajectory Prediction. Magnetic Resonance in Medicine, 2015, In Press.

5. Christoph Barmet, Nicola De Zanche, and Klaas P. Pruessmann. Spatiotemporal Magnetic Field Monitoring for MR, Magnetic Resonance in Medicine, 2008, 60:187–197

6. David A. Porter and Robin M. Heidemann. High resolution diffusion-weighted imaging using readout-segmented echo-planar imaging, parallel imaging and a two-dimensional navigator-based reacquisition. Magnetic Resonance in Medicine, 2009, 62:468–475.

7. Klaas P. Pruessmann, Markus Weiger, Peter Börnert, and Peter Boesiger. Advances in Sensitivity Encoding With Arbitrary k-Space Trajectories. Magnetic Resonance in Medicine, 2001, 46:638-651

8. Jackson JI, Meyer CH, Nishimura DG, Macovski A. Selection of a convolution function for Fourier inversion using gridding [computerised tomography application]. IEEE Trans Med Imaging, 1991, 10:473-478

9. Man L-C, Pauly JM, Macovski A. Multifrequency interpolation for fast off-resonance correction. Magnetic Resonance in Medicine, 1997, 37:785-792

Figures

Fig. 1: Schematic overview of the simulation framework. A simulated MR signal is created based on a measured trajectory, a given brain image, corresponding coil sensitivity maps and with/without a $$$B_0$$$ fieldmap. The reconstruction is performed based on the measured, GIRF-predicted or nominal trajectory and the known coil sensitivities, together with the $$$B_0$$$ map when relevant.

Fig. 2: Nominal, GIRF-predicted and measured trajectories of a RS-EPI (top) and a spiral (bottom) sequence. The GIRF predicted trajectories are based on modeling the gradient chain as a linear time-invariant (LTI) system^3,4. Zoomed insets show that for both sequences the measured trajectories deviate from the nominal ones and the GIRF-predicted trajectories is able to capture most of these discrepancies. Residual differences between the GIRF-predicted and the nominal is likely due to system nonlinearities, which can not be modeled using a LTI framework.

Fig. 3: RS-EPI: reconstruction performed using nominal, GIRF-predicted and measured trajectories without (top) and with (bottom) $$$B_0$$$ fieldmap. The difference compared to the original image is shown below the respective reconstruction. The difference images are scaled to +/-10% of the maximum value in the original image. Red arrows in the zoomed images point to an example region of increased artifact in the presence of $$$B_0$$$ inhomogeneities. Note that $$$B_0$$$ correction was used for all reconstructions with $$$B_0$$$ inhomogeneity and the increase in artifact is driven by the interaction of incorrect k-space sample locations with $$$B_0$$$ inhomogeneity.

Fig. 4: Spiral: reconstruction performed using nominal, GIRF-predicted and measured trajectories without (top) and with (bottom) a $$$B_0$$$ fieldmap. The difference compared to the original image is shown below the respective reconstruction. The difference images are scaled to +/-10% of the maximum value in the original image. The zoomed images highlight the ringing and blurring artifacts, which are pronounced in the image using the nominal trajectory and substantially reduced when using the GIRF-predicted one.

Tab. 1: RMSE of nominal vs. measured and GIRF-predicted vs. measured trajectories (first column) for the spiral and the RS-EPI sequence. RMSE of nominal, predicted and measured images vs. the original image, without (second column) and with (third column) a $$$B_0$$$ fieldmap.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

3917