3906

Encoding of Inductively Measured k-Space Trajectories in MR Raw Data
Jan Ole Pedersen1,2, Christian G. Hanson, Rong Xue3, and Lars G. Hanson1,2

1Centre for Magnetic Resonance, DTU Elektro, Technical University of Denmark, Kgs Lyngby, Denmark, 2Danish Research Centre for Magnetic Resonance, Centre for Functional and Diagnostic Imaging and Research, Copenhagen University Hospital, Hvidovre, Denmark, 3Institute of Biophysics, Chinese Academy of Sciences, State Key Laboratory of Brain and Cognitive Science, Beijing, People's Republic of China

Synopsis

For reconstruction of MRI from raw data, the k-space trajectory is needed. We propose to measure this simultaneously with the MRI signal using novel hardware and the scanner itself. As a first step, we demonstrate real-time processing of a gradient pickup coil voltage during scanning, modulation of this signal to a frequency within the MR acquisition bandwidth, and signal extraction from MR raw data. This principle is applied to measure k-space trajectories inductively and perform image reconstruction based on this. The resulting images have comparable quality to images reconstructed using nominal k-space trajectories. The method can potentially provide generic image reconstruction with limited hardware, even for challenging and dynamically updated gradient schemes.

Introduction

By measuring k-space trajectories, $$$k(t)$$$, MRI reconstruction can be performed without knowledge of sequence details and hardware imperfections. Using the scanner itself for measuring $$$k(t)$$$ alleviates timing challenges arising when using external equipment. This is exploited for MR-based gradient measurement[1]. The time derivate, ε, of the gradient field $$$G(t)$$$ can alternatively be measured inductively by a pickup coil. For a gradient echo sequence $$k(t) = \frac{\gamma}{2\pi} \int_0^t G(\tau) d\tau,$$which implies $$k(t) \propto \int_0^t \int_{t_{G0}} ^{\tau_1} \varepsilon (\tau_2) d\tau_2 d\tau_1,$$ where $$$t=0$$$ is the center of the relevant excitation pulse, and $$$t_{G0}$$$ a time point where the gradients are zero. The signal/trajectory synchronization challenge can be addressed by using the scanner itself for the acquisition, which also limits hardware requirements. Non-MR signals like $$$k(t)$$$ can be encoded in the MR data using amplitude modulation (AM) to a frequency in the oversampled range (sampled by the scanner, but not in FOV) without interference with MRI[2]. The encoded signal can be extracted by analyzing raw data, possibly while MRI is performed.

Method

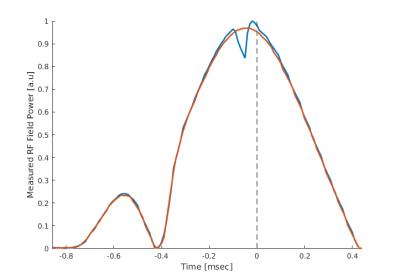
We have developed circuitry for sampling and real-time processing of non-MR signals. The processed signals are amplitude modulated onto an RF carrier detectable by an MRI scanner. The circuitry has three analog input channels (20 kHz bandwidth) and also measures a radio frequency (RF) power correlate for the 50MHz–1GHz range. The received digitized signals are processed by a Field Programmable Gate Array (FPGA), that controls an RF output channel where amplitude, phase, and frequency of up to 130MHz can be manipulated. Two-way communication for signals and hardware control is supported through USB connection to a computer. For proof of concept, the circuitry was used to acquire the k-space trajectory for an EPI sequence using a 3T Philips Achieva MRI system (208x127 receive matrix, 32 slices, TE/TR: 45/3000ms, 16% ramp sampling, echospacing: 0.62ms). See Fig.1 for experimental setup. Signal received from a pickup coil placed in the gradient field was integrated twice by the FPGA to obtain $$$k(t)$$$ with minimal delay (20us), and was send wirelessly to the scanner via its 32 channel head receive coil. To facilitate detection, a central sample in the excitation pulse wave form was nulled through pulse programming (see Fig.2). This special RF signature was detected by the RF detector of the circuitry, and triggered nulling of $$$t$$$ and $$$t_{G0}$$$ in the integrals. The k-space contributions from the readout and phase encoding gradients were determined separately by turning on the gradients one by one. As a simple way to compensate the 20us signal delay during FPGA processing, the last 8 MR sample points from each readout period were not used in the image reconstruction. Inaccurate determination of the RF pulse center was corrected, before averaging $$$k(t)$$$ across measurements performed over 5 volumes of 32 slices extracted from a single receive channel. Lowpass filtering reduced noise contributions affecting $$$k(t)$$$ estimates. The known FOV was used to determine the otherwise unknown scaling between the double integral and $$$k(t)$$$.

Results

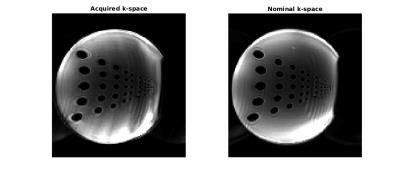
Using non-uniform Fourier reconstruction (NUFFT)[3], MRI data acquired in a separate EPI scan of a phantom were reconstructed using measured and nominal k-space trajectories (Fig.3).

Discussion and Conclusion

Through the use of developed circuitry for non-MR signal sampling, processing and amplitude modulation, we have demonstrated measurement of k-space trajectories using the MR scanner itself. The method is flexible and requires limited hardware of general interest for real-time applications. 20us of each sampling period was discarded which has little influence on reconstructed images, since the missing samples are at the outer regions of sampled k-space. Ramp-sampling reduces the corresponding, limited loss. RF waveforms were modified to trigger resetting of integrators, but since the scaled RF power is measured, a power calibration can alternatively be used to monitor continuously updated amplitude integrals to detect the pulse center for resonant pulses. This would also facilitate k-space trajectory measurements for sequences with multiple RF pulses per excitation, e.g. spin-echo. The broadband k-space signal was passed wirelessly to the scanner, so simultaneous MRI acquisition was unattractive due to interference. Directly connecting the developed circuitry to a receive channel of the scanner alleviates this, and likely also improves SNR. For an EPI sequence the method performed comparably to using the nominal k-space trajectory, but advantages may likely result for challenging trajectories such as spiral-in EPI. No attempts to limit RF noise was made for this prototype hardware implementation that emitted non-white RF noise here reduced by averaging and limited filtering. The quality of images reconstructed from nominal and measured gradients were nevertheless of comparable quality, and the results are encouraging.

Acknowledgements

No acknowledgement found.

References

1. Duyn J et. al. Simple Correction Method for k-Space Trajectory Deviations in MRI. J. Magn. Reson. 1998;132:150-153

2.Hanson et al. Encoding of Electrophysiology and Other Signals in MR Image. JMRI. 25.2007;25:1059-1066

3. Fessler A. Nonuniform Fast Fourier Transforms Using Min-Max Interpolation. IEEET-SP 2003;51(2):560-74

Figures

Fig.1: Experimental setup used for acquiring k-space trajectories. A pickup coil is placed in the gradient field of the MR scanner, and signals induced by gradient switching are processed by the FPGA. This also controls the carrier generation and the amplitude modulation (AM). In the FPGA, a double integration of the signal is performed to obtain $$$k(t)$$$, which is transmitted to the head receive coil using a quarter-wavelength dipole antenna. A similar antenna is connected to monitor the RF pulses transmitted by the scanner. When the RF signature shown in Fig.2 is detected, the integrators are nulled.

Fig.2: Waveform of excitation pulses as measured by the developed circuitry. The RF pulse used for MRI excitation (red) was modified through pulse programming and measured (blue) by the circuitry to determine the center of the pulse. The power drop detection triggered nulling of the integrators used for determining $$$k(t)$$$. After calibration with a known pulse, the pulse center can alternatively be detected based on the amplitude integral.

Fig.3: NUFFT reconstructed EPI images using acquired (left) and nominal (right) k-space trajectories. Similar image quality was obtained, demonstrating the feasibility of acquiring k-space trajectories using the developed hardware and the scanner itself.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3906