Purpose

To develop a neural network-based approach for fast inference of B0 inhomogeneities from projection-encoded FID readouts.

Methods

We formulate a learning-based approach to the problem, where we use a neural network to perform the field map inference. We obtain the ground-truth field maps using a double-echo EPI sequence (TE = 13/25 ms, TR=50ms). Due to physiological motion such as breathing, we observe periodic field variations in the acquired field maps (see Fig. 2 and 3). Plain FID signals from multiple coil elements can be used to estimate head movements^1,2 and B0 field inhomogeneities⁴. We aim to infer the field maps from projection-encoded FID readouts. To obtain those we augment a double-echo EPI sequence with three additional readouts (projection encoding in X, Y and Z directions), which are acquired directly after the slice refocusing gradient (see Fig. 1 for the sequence diagram). The FID readouts are inverse Fourier transformed, and the first readout is used as a phase reference. The phase difference is then calculated between each FID readout and the reference by division in the complex domain. The input to the neural network has the feature dimensionality of NxCxSx3, where N=128 is the readout length, C=30 is the number of coil elements, and S=12 is the number of partitions. We train the neural network to predict the field changes against the reference (field map of the first volume) rather than the absolute field maps. The neural network is composed of 5 fully connected linear recombination layers, which are interleaved with rectified non-linear activation units. We use 250 neurons in each layer, and train the network for 100 epochs with the Adadelta optimizer and a learning rate of 0.1. In total, our dataset consists of 1200 volumes (head scans), which are obtained from 8 healthy subjects (with informed consent and approval by the local ethics committee). Since the positioning of an excited slab can vary from subject to subject, we provide the coordinate of the center of the excited slab together with a normal vector that describes its orientation as additional inputs to the network. The data was acquired at 9.4T and the imaging was performed with a custom-built head coil³ (16 transmit / 31 receive channels).

Results

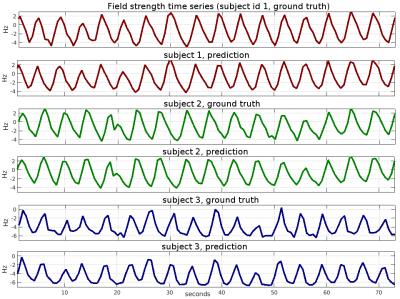
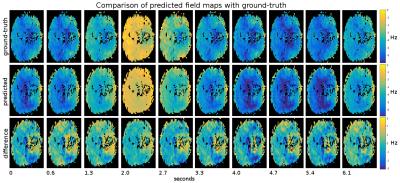
To evaluate the performance of our method, we compare the field map offsets predicted by the neural network against the ground truth. As an objective measure we use percentage-based L2 relative error norm, which is defined as 100*L2(x-y)/L2(y), where x is the output of the neural network, y is the ground truth field change map, and L2 is the Euclidean norm. In the first experiment, we split the entire set of 1200 volumes into 90% training and 10% test parts, which do not intersect. The volumes for training and testing are randomly picked. After training for 50 epochs, we observe that the test error stabilizes at 16%. The next experiment is similar to the first, except that instead of random volume selection, we take the last 10% of the volumes of the field map series in each subject. This way we test the ability of the network to generalize over the time course of the field changes. The relative test error we obtain is 17%. Finally, we test the ability of the network to generalize over subjects and brain morphologies. In this experiment, we train the network on the dataset composed of 7 subjects and evaluate the test error on the remaining single subject. We perform 8 runs, where we cycle the test subject so that the average error can be evaluated over the subjects. We obtain the relative error of 52%. In Fig. 2 we plot the field strength time series for three different voxels and three different subjects. We compare the ground-truth series against the predicted ones, and use the absolute field maps rather than field change maps. Additionally, we compare in Fig 3 the predicted and ground-truth 2D field maps (we show a single slice from a volume).

Discussion

In this work, we present a field map estimation technique that uses projection-based navigators. We show that it is possible to generalize the mapping from projection-FID to field maps over subjects and brain morphologies. Cross-subject generalization performance reaches 52% error rate, which makes the approach promising to be further explored and improved. The neural network that we use is relatively small, which means that underlying matrix-matrix multiplications can be performed sufficiently fast for the method to be used for real-time prediction. The follow-up research will aim at adapting the technique to dynamic shimming.

Acknowledgements

No acknowledgement found.