3885
Bayesian Experimental Design for Multi-Parametric T1/T2 Relaxometry and Diffusion1Translational Imaging Group, University College London, London, United Kingdom, 2Translational Imaging Group, University College London, 3Department of Medical Physics, University College London Hospitals, 4Dementia Research Centre, University College London
Synopsis
Multi-parametric imaging, such as joint relaxometry and diffusion, can allow for a time-efficient measurement of several parameters of interest. However, it is unclear how best to make use of valuable scanner time when using such novel imaging techniques. In this work, we explore how Bayesian experimental design can be used to derive a maximally time-efficient joint imaging experiment.
Introduction
Joint relaxometry and diffusion imaging offers rich information about structural and microstructural properties, but acquisitions are relatively time-consuming and have low SNR. Using Bayesian experimental design1, we find an optimal joint acquisition that offers the maximum amount of information possible in a given scan duration. Simulations show a large improvement in parameter accuracy from this acquisition, and these results are borne out by experimental validation using tissue phantoms, scanned with body coils to represent the challenging conditions of abdominal imaging.Methods
The measured signal is assumed to be related to the parameters of interest by the following model:
$$S = S_0 (1 - \exp{-R_1 * {TR}} \exp{-R_2 * {TE}} \exp{-b * {ADC}})$$.
To optimise the design, we formulate a utility function based upon the Fisher information [2], with $$$u(TR, TE, b) = \det{H}$$$, with $$$H_{i,j} = \sum_k \frac{1}{\sigma_k^2} \frac{\partial S}{\partial \theta_i} \frac{\partial S}{\partial \theta_j}$$$ and $$$\theta = (R1, R2, ADC)$$$.
As R1, R2 and ADC are not known ahead of time, we evaluate this utility’s expectation over broadly representative parameter priors: $R1 \sim \mathcal{N}(1.25, 0.1), R2 \sim \mathcal{N}(8.3, 2.0), ADC \sim \mathcal{N}(1.2E-3, 0.3E-3)$. Quadrature is performed using a pre-existing high-performance quadrature software package3, allowing for rapid evaluation of the utility function. Numerical optimisation is performed using a genetic algorithm3, subject to constraints upon the total scan duration. (The duration is estimated by summing the design's TRs.) This constrained optimisation leads to the optimal design in Figure 1. The reference design, by contrast, consisted of holding each of TR, TE and b constant at $$$(5000ms, 100ms, 0 mm/s)$$$ respectively, then varying each parameter in equal increments in the following ranges: $$$(3000:300:5000ms, 96:30:150ms, 0:100:600mm/s)$$$. Both acquisitions were five minutes long.
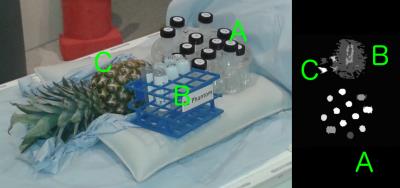
Monte Carlo simulations were performed to assess performance of the method compared to an equally-spaced reference experiment with SNR=0.5 — a decreased root mean square error indicates superior performance, as set out in Figure 1. Subsequently, experimental data were gathered using a 1.5T Siemens scanner using 2D-EPI, measuring phantoms of different R1/R2/ADC values as shown in Figure 2. These were compared for inter-method consistency, with intra-method variance assessed from voxelwise variance in each case.
Results and Discussion
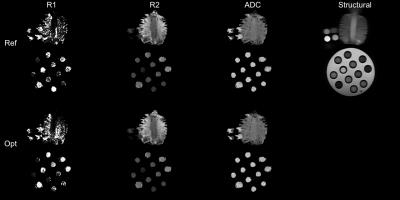
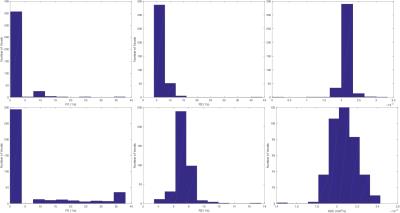
Figure 3 shows example images with per-voxel fits, for both optimised and reference designs, next to a structural image for reference. Visually, there is reasonable agreement between the two designs, with qualitatively similar patterns of R1/R2/ADC across the samples. R1 estimates are particularly noisy — this is commonly observed to be the case in joint relaxometry acquisitions, and is unsurprising. Figure 4 shows example per-voxel distributions of parameters within an ROI. Whereas R2 and ADC are approximately normally distributed, R1 clearly is not. To some extent, this explains the poor performance of the optimised design for measuring R1 (despite superior performance for measuring R2 and ADC) within these experiments.
Figure 5 shows the agreement in average R1/R2/ADC values between the optimised and reference designs. There is relatively good agreement for R2 and ADC, whereas R1 has poorer agreement. This is likely because these R1 values are further from the design prior, in addition to the challenge of measuring R1 under these constraints.
There is reasonable agreement between the values estimated by the two designs, particularly for R2 and ADC. For R1, the agreement is worse, which is not entirely unexpected given the difficulty in measuring R1 with this approach. Variance is reduced in the R2 and ADC estimates, which supports the predictions from simulations that the design optimisation improves estimation for these parameters. Moreover, parameter distributions are more often found to be at plausible values when the optimised design is used (Figure 4), further supporting the idea that it increases estimation performance of parameters within the plausible range as specified by the prior.
Conclusion
Because of the high cost of scanner time, it is important to maximise the utility of a scan. Optimal design theory can inform the planning of imaging experiments, allowing more accurate parameter estimates to be acquired within a given scanning duration by tailoring scanning parameters to match prior beliefs. Here we began to examine optimal design approaches for joint imaging of T1/T2 relaxometry and diffusion, using broad physiological priors, although it could conceivably be done for more specific individual priors. Future work will validate these results in vivo.Acknowledgements
DO and DLT are supported by the UCL Leonard Wolfson Experimental Neurology Centre (PR/ylr/18575). We would also like to acknowledge the MRC (MR/J01107X/1), the National Institute for Health Research (NIHR), the EPSRC (EP/H046410/1) and the National Institute for Health Research University College London Hospitals Biomedical Research Centre (NIHR BRC UCLH/UCL High Impact Initiative BW.mn.BRC10269). This work is supported by the EPSRC-funded UCL Centre for Doctoral Training in Medical Imaging (EP/L016478/1). The Dementia Research Centre is supported by Alzheimer’s Research UK, Brain Research Trust, and The Wolfson Foundation.References
[1] Chaloner, K., & Larntz, K. (1989). Optimal Bayesian design applied to logistic regression experiments. Journal of Statistical Planning and Inference, 21(2), 191-208.
[2] Owen, D., Melbourne, A., Thomas, D., De Vita, E., Rohrer, J., & Ourselin, S. (2016, October). Optimisation of Arterial Spin Labelling Using Bayesian Experimental Design. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 511-518). Springer International Publishing.
[3] Hahn, T. (2005). Cuba—a library for multidimensional numerical integration.Computer Physics Communications, 168(2), 78-95.
[4] Johnson, S. The nonlinear-optimization package, http://ab-initio.mit.edu/nlopt
Figures