3878
GenSeT: Reconstruction of k-space under-sampled DCE-MRI data using high-order generalized series and temporal constraint1Electrical Engineering & Information Technology, Vietnamese-German University, Binh Duong New City, Vietnam, 2Department of Radiology, Mayo Clinic Arizona, Scottsdale, AZ, United States, 3Advanced Imaging Research Center, Oregon Health & Science University, Portland, OR, United States
Synopsis
A novel reconstruction method exploiting high-order generalized series and temporal sparsity constraint has been presented for sparsely-sampled DCE-MRI. The method uses a static reference to model high-resolution anatomical structures while extrapolating the missing k-space and imposing the sparsity of the time frame difference. Our initial experience with human breast DCE-MRI data shows that the proposed GenSeT method yields more accurate spatiotemporal dynamics and PK analysis than the conventional zero-filling and TWIST reconstruction methods. Further validation of the method as a useful reconstruction approach for sparsely-sampled DCE-MRI is warranted in a larger cohort and with data from different organs.
INTRODUCTION
Clinical breast DCE-MRI protocols using conventional full
k-space sampling GRE sequence have high spatial resolution due to the need for morphology
evaluation, but low temporal resolution, rendering
quantitative pharmacokinetic (PK) analysis of DCE-MRI data inaccurate and
impractical. The commercial TWIST sequence yields high spatial and temporal resolutions simultaneously by under-sampling
the k-space and copying the missing
data from the neighboring time frames. If the
signal temporal variation is significant due to contrast uptake and washout, data
sharing may result in image artifacts, precluding measurement of true signal
enhancement dynamics and accurate PK analysis. In this work, a
novel reconstruction method using high-order
generalized series combined with temporal sparsity constraint, coined GenSeT (Generalized Series with
Temporal constraint), is developed to extrapolate (instead of copying) the missing
k-space. Simulation reconstruction of
human breast DCE-MRI data was performed to assess accuracies
of various reconstruction methods in estimating spatiotemporal variations and PK
parameters.THEORY
To improve DCE-MRI temporal resolution, under-sampling of k-space has been proposed.1-3 An alternative method is to exploit the generalized series (GS) model, which has been demonstrated to be effective for the sparsely-sampled fMRI.4 This method uses a static high-resolution reference and represents missing dynamic components using the GS basis functions. Specifically, a 3D DCE image at a certain time point is represented as $$\rho(\boldsymbol{r},t)=I_{ref}(\boldsymbol{r})\sum_{l=-L/2}^{L/2+1}c_l(t)e^{-j 2 \pi l \boldsymbol{\triangle k} \cdot \boldsymbol{r}},$$ where $$$ \boldsymbol{\triangle k}$$$ represents sampling interval and $$$c_l(t)$$$ provides temporal data adaptation.5 In the conventional use of the model employed by the RIGR method,6 the low-order GS basis functions were used. We found that a high order $$$L$$$ is critical in allowing the model to capture temporal dynamics.4 A data extrapolation using such GS model leads to an inevitable over-modeling, thus an additional temporal constraint is imposed by noting that the difference between successive time frames is sparse.7 Specifically, we minimize the following cost function: $$\boldsymbol{\widehat{c}} = \text{arg} \min_{\boldsymbol{c}} ||\boldsymbol{d}-\boldsymbol{S}\boldsymbol{\Psi}\boldsymbol{c}||_2^2 + \lambda ||\boldsymbol{D} \boldsymbol{\Psi} \boldsymbol{c} ||_1,$$ where $$$\boldsymbol{d}$$$ is the measurement k-space data, $$$\boldsymbol{S}$$$ is the measurement and sampling operator, $$$\boldsymbol{\Psi}$$$ is the operator whose columns are the GS basis functions, $$$ \boldsymbol{D}$$$ is the temporal difference operator, and $$$\lambda$$$ is the regularization parameter. Having estimated $$$\boldsymbol{\widehat{c}}$$$, one can reconstruct the corresponding image using the GS model. The procedure is repeated to reconstruct every time frame in the dataset. The proposed optimization problem can be solved using the Nesterov's gradient-descent method.8METHODS & RESULTS
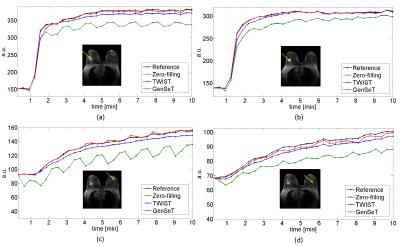
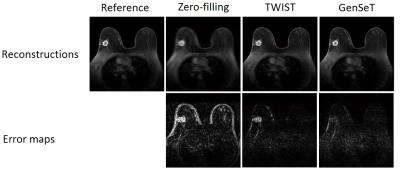
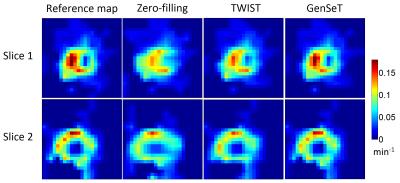
A sub-image set of 64×64 in-plane resolution and 31 slices of 1.4 mm thickness, covering the spatial extent of a biopsy-proven malignant tumor, was extracted as the reference image set from a human bilateral breast DCE-MRI dataset using a TWIST GRE sequence (TE/TR = 2.9/6.1 ms, 32 time frames).9 Under-sampling in $$$(kz,ky)$$$ was performed as follows: (i) the first time frame, serving as a reference in the GS model, was fully sampled; (ii) starting from the second frame, successive sampling along each of the four variable-density spiral segments was applied.10 The union of these four spirals covers the whole k-space. Under-sampled data was subject to the zero-filling (missing k-space points are replaced by zeros), TWIST (missing k-space points are copied from those at the neighboring time frames), and proposed GenSeT reconstructions. Fig. 1 shows the resulting intensity time series in the malignant tumor and contralateral normal parenchyma regions. The GenSeT method improved the accuracy of the time course while the TWIST method under-estimated the uptake slope, possibly due to the data-copying scheme, thus not reflecting the true temporal dynamics. The spatial error maps between the reconstructed and reference image sets, shown in Fig. 2, indicate that the TWIST method yielded a higher error than the GenSeT method in the tumor region, particularly at the boundary. The PK analysis of the DCE data was performed using the standard Tofts model and the resulting tumor Ktrans maps are shown in Fig. 3. Underestimation of voxel Ktrans values due to the TWIST reconstruction can be observed, while the zero-filling method yielded the worst accuracy.DISCUSSION & CONCLUSIONS
A novel reconstruction method exploiting high-order generalized series and temporal sparsity constraint has been presented for sparsely-sampled DCE-MRI. The method uses a static reference to model high-resolution anatomical structures while extrapolating the missing k-space and imposing the sparsity of the time frame difference. Our initial experience with human breast DCE-MRI data shows that the proposed GenSeT method yields more accurate spatiotemporal dynamics and PK analysis than the conventional zero-filling and TWIST reconstruction methods. Further validation of the method as a useful reconstruction approach for DCE-MRI is warranted in a larger cohort and with data from different organs.Acknowledgements
The authors gratefully acknowledge grant support from the VGU grant PSSG No. 1, AFOSR/AOARD grant 16IOA006, and NIH grant U01 CA154602.References
[1] Tudorica L, Oh K, Roy N, et al. A feasible high spatiotemporal resolution breast DCE-MRI protocol for clinical settings. Magn. Reson. Imag. 2012;30:1257–1267.
[2] Chen L, Schabel M, DiBella E. Reconstruction of dynamic contrast enhanced magnetic resonance imaging of the breast with temporal constraints. Mang. Reson. Imag. 2010;28:637–645.
[3] Brinegar C, Schmitter S, Mistry N, et al. Improving temporal resolution of pulmonary perfusion imaging in rats using the partially separable functions model. Magn. Reson. Med. 2010;64:1162–1170.
[4] Nguyen H and Glover G. A modified generalized series approach: Application to sparsely sampled fMRI. IEEE Trans. BioMed. Eng. 2013;60:2867-2877.
[5] Liang ZP and Lauterbur P. An efficient method for dynamic magnetic resonance imaging. IEEE Trans. Med. Imag. 1994;13: 677–686.
[6] Chandra S, Liang ZP, Webb A, et al. Application of reduced-encoding imaging with generalized-series reconstruction (RIGR) in dynamic MR imaging. J. Magn. Res. Imag. 1996;6:783-797.
[7] Otazo R, Candés E, Sodickson D. Low-rank plus sparse matrix decomposition for accelerate dynamic MRI with separation of background and dynamic components. Magn. Reson. Med. 2015;73:1125–1136.
[8] Becker S, Bobin J, Candés E. NESTA: A fast and accurate first order method for sparse recovery. SIAM J. Imag. Sci. 2011;4:1-39.
[9] A. Tudorica, Oh K, Chui S, et al. Early prediction and evaluation of breast cancer response to neoadjuvant chemotherapy using quantitative DCE-MRI. Transl. Oncol. 2016;9:8-17.
[10] Chang C and Glover G. Variable-density spiral-in/out functional magnetic resonance imaging. Magn. Reson. Med. 2011;65:1287–1296.
Figures