3875

Joint Reconstruction of Multi-Contrast Images: Compressive Sensing Reconstruction using both Joint and Individual Regularization Functions

Emre Kopanoglu¹, Alper Gungor¹, Toygan Kilic^2,3, Emine Ulku Saritas^2,3, Tolga Cukur^2,3, and H. Emre Guven¹

¹Aselsan Research Center, Ankara, Turkey, ²Electrical and Electronics Engineering, Bilkent University, Turkey, ³National Magnetic Resonance Research Center (UMRAM), Bilkent University, Turkey

Synopsis

In many clinical settings, multi-contrast images of a patient are acquired to maximize complementary information. With the underlying anatomy being the same, the mutual information in multi-contrast data can be exploited to improve image reconstruction, especially in accelerated acquisition schemes such as Compressive Sensing (CS). This study proposes a CS-reconstruction algorithm that uses four regularization functions; joint L1-sparsity and TV-regularization terms to exploit the mutual information, and individual L1-sparsity and TV-regularization terms to recover unique features in each image. The proposed method is shown to be robust against leakage-of-features across contrasts, and is demonstrated using simulations and in-vivo experiments.

Introduction

Compressive Sensing (CS) uses randomly undersampled acquisitions to yield incoherent aliasing artifacts, and a nonlinear reconstruction to suppress these artifacts^1-7. In many MRI applications, multi-contrast images are acquired together to maximize diagnostic information, since different contrast mechanisms provide complementary information. With the underlying anatomy being the same, previous studies have demonstrated advantages of joint reconstruction of these multi-contrast images^5-7. While earlier methods enforced sparsity individually on each acquisition, recent reconstruction have leveraged joint-sparsity terms across acquisitions to improve image quality^5,7.

In this study, we present an adaptation of the Alternating Direction Method-of-Multipliers⁸ for joint reconstruction of multi-contrast images. As opposed to previous CS-algorithms, the proposed method uses four regularization functions; L1-sparsity and TV-regularization for individual contrasts, and Color-TV⁹ and Group-L1-sparsity⁵ imposed on all contrasts simultaneously. Joint sparsity/TV terms recover information shared across acquisitions while individual terms recover features unique to each contrast.

Methods

The proposed method uses Color-TV⁹ and Group-L1-sparsity⁵ (Eqs. [3]-[4]) to enhance correlated features and individual TV and L1 functions (Eqs. [5]-[6]) to facilitate recovery of individual features via the following optimization framework.

Solve:

$$\min_x\alpha CTV(x)+\beta GSp(x)+\sum_i\gamma TV\left(x^{(i)}\right)+\sum_i\theta Sp\left(x^{(i)}\right)$$

subject to

$$\Vert Ax_i-y\Vert_2<\epsilon_i$$

where

$$CTV(x)=\sum_n\sqrt{\sum_{i=1}^k\left(\nabla_1\vert x^{(i)}[n]\vert\right)^2+\left(\nabla_2\vert x^{(i)}[n] \vert\right)^2}$$

$$GSp(x)=\sum_n\sqrt{\sum_{i=1}^k\left( x^{(i)}[n]\right)^2}$$

$$TV(x^{(i)})=\sum_n\sqrt{\left(\nabla_1\vert x^{(i)}[n]\vert\right)^2+\left(\nabla_2\vert x^{(i)}[n]\vert\right)^2}$$

$$Sp(x^{(i)})=\sum_n\vert x^{(i)}[n]\vert$$

where, $$$ \alpha,\beta,\gamma,\theta $$$ denote regularization weight parameters. $$$\epsilon_i^2$$$ (noise energy for contrast i) can be calculated in practice from data acquired via a rapid excitation-less acquisition.

Two different versions of the above framework were implemented for individual (ASEL-CS-indiv) and joint (ASEL-CS-j) reconstruction of multi-contrast images. Both were compared to the following state-of-the-art CS reconstructions: SparseMRI¹, recPF³, TVCMRI², GSMRI⁵, FCSA⁴, FCSA-MT⁷. The undersampling masks were generated using probability-density-functions that decay with the third-order of the linear-distance/radius (for one-/two-dimensional undersampling) in k-space. One-eighth of the central k-space was fully-sampled. The same set of masks were used in all methods, but different masks were generated for each contrast. Image-quality metrics used were; structural-similarity-index (SSIM), peak signal-to-noise-ratio (pSNR), normalized-root-mean-squared-error (nRMSE), mean-magnitude-error (mmE).

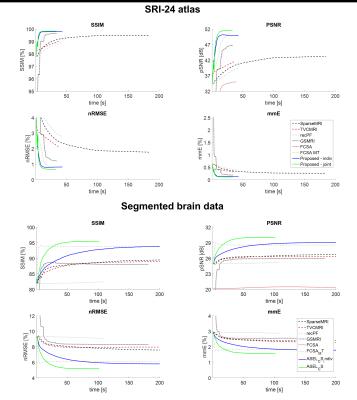
Simulation 1: Same settings as Ref⁷; real and noiseless images (SRI-24 atlas¹⁰), 100 iterations, $$$\alpha$$$=0.01,$$$\beta$$$=0.035 for all methods, $$$\gamma=\theta$$$=0 (no individual terms for ASEL-CS-j¹¹).

Simulation 2: Complex and noisy images (Ref¹²: segmented brain, 11 tissues), 250 iterations. Regularization parameters were optimized for each method (interval-search algorithm seeking maximum SSIM). For ASEL-CS-j, $$$\alpha,\beta$$$ were optimized as above for $$$\gamma=\theta$$$=0, and $$$\gamma,\theta$$$ were manually tuned afterwards.

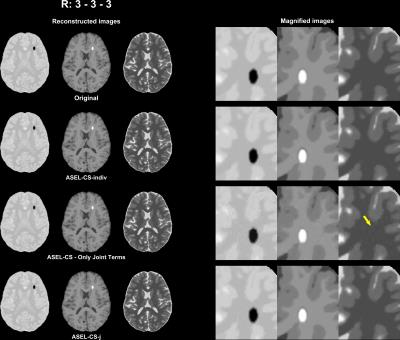
Simulation 3: A potential pitfall in joint reconstruction is leakage of distinct features among images. ASEL-CS-j was tested against this pitfall by introducing distinct artificial tissues to the images.

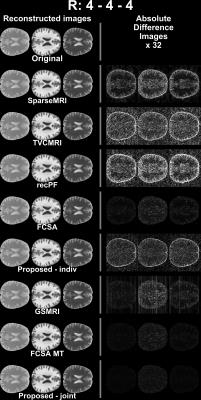
In-vivo Experiment: Experiments were conducted on a 3T scanner (Siemens Healthcare, Erlangen). Full k-space data (32-channel receiver) were acquired, subsampled retrospectively, reconstructed separately for each channel for each method using optimized parameters, and combined using the algorithm given in Ref¹³. The images were normalized to the range [0, 255] for each channel and each contrast to avoid parameter mismatch. The channel-combination algorithm¹³ automatically handled the amplification of signals from farther channels due to this normalization.

Results

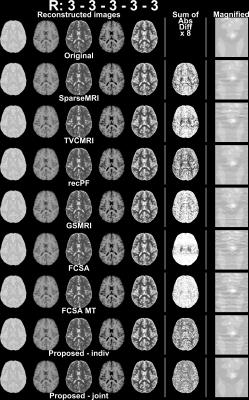
ASEL-CS-j achieves visibly reduced reconstruction errors (Figure 1) and improved artifact suppression (Figure 2) compared to alternative methods on simulated brain images. Furthermore, ASEL-CS-j has the highest convergence speed to its optimal performance in the SRI24-phantom (Figure 3a). While RecPF has a better initial convergence rate in the numerical brain phantom, ASEL-CS-j surpasses RecPF within 10-20 seconds of computation time, and yields higher image quality after convergence (Figure 3b). Figure 4 shows that ASEL-CS-j has no visible artifacts due to undesired leakage-of-features across contrasts. Similarly, for in-vivo reconstructions, ASEL-CS-j yields higher-quality images with detailed tissue depiction compared to all remaining methods, including its closest competitor FCSA-MT (Figure 5).

Discussion

The proposed method uses four distinct regularization functions: individual L1-sparsity and TV-regularization, and joint L1-sparsity and TV-regularization. In contrast, GSMRI uses only group L1-sparsity and FCSA-MT uses only the joint terms. In ASEL-CS-j, joint penalty terms exploit the correlated features across images, while individual terms enable recovery of distinct features in each image.

The proposed method outperformed state-of-the-art CS reconstructions in all datasets reported here. Furthermore, our results indicate that ASEL-CS-j is robust against leakage-of-features across images. We observed that omission of individual penalty terms led to leakage-of-features across contrasts, minor albeit visible. Yet, the simultaneous use of both individual and joint terms suppressed these artifacts effectively.

To ensure that similar penalty weights and reconstruction parameters work well, in-vivo data were normalized to the same intensity range in the image domain. Although this led to different noise-floors across contrasts, it was observed that this normalization is critical to improve convergence behavior across all methods implemented here.

Acknowledgements

The authors would like to thank the authors of the methods SparseMRI¹, recPF³, TVCMRI², GSMRI⁵, FCSA⁴ and FCSA-MT⁷ for making the source codes of their algorithms available online.

References

1. Lustig, M., Donoho, D., Pauly, J. M. Sparse Mri: The Application of Compressed Sensing for Rapid Mr Imaging. Magnetic Resonance in Medicine. 2007;58(6):1182-1195. doi: 10.1002/mrm.21391.

2. Shiqian, M., Wotao, Y., Yin, Z., Chakraborty, A., editors. An Efficient Algorithm for Compressed Mr Imaging Using Total Variation and Wavelets. Computer Vision and Pattern Recognition, 2008 CVPR 2008 IEEE Conference on; 2008 23-28 June 2008.

3. Yang, J., Zhang, Y., Yin, W. A Fast Alternating Direction Method for Tvl1-L2 Signal Reconstruction from Partial Fourier Data. IEEE Journal of Selected Topics in Signal Processing. 2010;4(2):288-297. doi: 10.1109/JSTSP.2010.2042333.

4. Huang, J., Zhang, S., Metaxas, D. Efficient Mr Image Reconstruction for Compressed Mr Imaging. Medical Image Analysis. 2011;15(5):670-679. doi: http://dx.doi.org/10.1016/j.media.2011.06.001.

5. Majumdar, A., Ward, R. K. Joint Reconstruction of Multiecho Mr Images Using Correlated Sparsity. Magnetic Resonance Imaging. 2011;29(7):899-906. doi: http://dx.doi.org/10.1016/j.mri.2011.03.008.

6. Bilgic, B., Goyal, V. K., Adalsteinsson, E. Multi-Contrast Reconstruction with Bayesian Compressed Sensing. Magnetic Resonance in Medicine. 2011;66(6):1601-1615. doi: 10.1002/mrm.22956.

7. Huang, J., Chen, C., Axel, L. Fast Multi-Contrast Mri Reconstruction. Magnetic Resonance Imaging. 2014;32(10):1344-1352. doi: http://dx.doi.org/10.1016/j.mri.2014.08.025.

8. Guven, H. E., Gungor, A., Cetin, M. An Augmented Lagrangian Method for Complex-Valued Compressed Sar Imaging. IEEE Transactions on Computational Imaging. 2016;2(3):235-250. doi: 10.1109/TCI.2016.2580498.

9. Bresson, X., Chan, T. Fast Dual Minimization of the Vectorial Total Variation Norm and Applications to Color Image Processing. Inverse Problems and Imaging. 2008;2(4):455-484.

10. Rohlfing, T., Zahr, N. M., Sullivan, E. V., Pfefferbaum, A. The Sri24 Multichannel Atlas of Normal Adult Human Brain Structure. Human Brain Mapping. 2010;31(5):798-819. doi: 10.1002/hbm.20906.

11. Gungor, A., Kopanoglu, E., Cukur, T., Guven, H. E., editors. Fast Recovery of Compressed Multi-Contrast Magnetic Resonance Images. SPIE Medical Imaging; 2017; Orlando, FL, USA.

12. Aubert-Broche, B., Griffin, M., Pike, G. B., Evans, A. C., Collins, D. L. Twenty New Digital Brain Phantoms for Creation of Validation Image Data Bases. IEEE Trans Med Imaging. 2006;25(11):1410-1416. Epub 2006/11/23. doi: 10.1109/tmi.2006.883453. PubMed PMID: 17117770.

13. Walsh, D. O., Gmitro, A. F., Marcellin, M. W. Adaptive Reconstruction of Phased Array Mr Imagery. Magnetic Resonance in Medicine. 2000;43(5):682-690. doi: 10.1002/(SICI)1522-2594(200005)43:5<682::AID-MRM10>3.0.CO;2-G.

Figures

Figure 1: Methods were compared using PD, T1 and T2 images from the SRI24 atlas for 4-fold 2D-acceleration. The same settings were used for all methods as in Ref7: images were real and noiseless, FoV: 240x240mm, image size: 256x256, all images were normalized to the range [0,255], 100 iterations were used for each method. In contrast to Ref7, pixel values were not enforced to integer values here. For the proposed method, individual sparsity functions were not used. Lower-intensity difference images demonstrate improved reconstruction performance for the proposed joint reconstruction algorithm ASEL-CS-j.

Figure 2: Methods were compared using complex and noisy images (image size: 256x256, FoV: 256x256mm) and 3-fold one-dimensional (vertical direction) acceleration. Regularization function weights were optimized using an automated interval search algorithm for all methods. Noise was generated using a normal distribution and a standard deviation equal to 10% of the mean k-space intensity across all contrasts. 250 iterations were used for each method. Magnified PD-images demonstrate improved artifact suppression for ASEL-CS-j.

Figure 3: Image metrics plotted with respect to computation time for the SRI-24 atlas (Fig. 1) and the numerical brain phantom (Fig. 2). Runtime measurements were taken from Matlab for each method using cputime and summed through iterations, averaged over different contrasts. Computation times indicate the cumulative runtime of the reconstruction algorithms, excluding data preparation, since data were pre-processed for all methods. All metrics were averaged across contrasts. 100 iterations were used for the SRI-24 atlas simulations and 250 iterations for the numerical brain phantom simulations.

Figure 4: The proposed method was tested against undesired feature leakage during joint reconstruction. For this purpose, distinct artificial features were introduced to the initial images in the shape of elliptical low-intensity and high-intensity regions in PD- and T1-images, respectively. When only the joint regularization terms were used, leakage artifacts were visible (arrow). The individual regularization terms of the proposed method suppress leakage artifacts. The reconstructed images show no visible artifacts in and around the region of the artificially introduced tissues, demonstrating the robustness of the method.

Figure 5: In-vivo results. Arrows indicate sharper recovery of features with the joint reconstruction algorithm, ASEL-CS-j. Fully-sampled data were acquired using a 32-channel receive-array, and undersampled retrospectively using different masks for each contrast but the same set of masks for each method and channel. Reconstructions were performed separately for each channel, i.e., joint reconstruction methods jointly reconstructed PD, T1, T2 data for each channel, and then those 32 images were combined for each method and each contrast. 2.5-fold two-dimensional undersampling masks were used. Phase x Readout x Slice FoV: 192x256x176mm, resolution:1x1x2mm. The optimized regularization parameters were used in reconstruction.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

3875