3873

Highly Accelerated Quantitative MRI with ICTGV Regularized Reconstruction
Matthias Schloegl1, Martin Holler2, Oliver Maier1, Thomas Benkert3, Kristian Bredies2, Kai Tobias Block3, and Rudolf Stollberger1

1Institute of Medical Engineering, Graz University of Technology, Graz, Austria, 2Institute of Mathematics and Scientific Computing, University of Graz, Austria, 3Center for Advanced Imaging Innovation and Research (CAI2R), Department of Radiology, New York University School of Medicine, New York, NY, United States

Synopsis

This work describes the use of ICTGV regularization for highly accelerated T1 and T2 quantification. For increased robustness of quantitative MRI multiple parameter encodings are necessary. With conventional encoding, this strategy increases scan time, in particular for T1. By using appropriate subsampling and iterative image reconstruction with ICTGV regularization, high quantification quality is achieved up to an acceleration factor of 16.

PURPOSE

The promise of quantitative MRI (qMRI) for gaining more specific and sensitive tissue-property information (biomarkers) has triggered the development of many new data acquisition and analysis methods. One important aspect is the acceleration of qMRI such that clinically feasible scan times are achieved. This issue has been addressed by undersampling data and using parallel imaging, compressed sensing1,2 and model-based3,4 reconstruction. When acquiring the data with increasing parameter-encoding strength, it is possible to treat the parameter dimension of qMRI as temporal dimension in the reconstruction. Therefore, we investigate ICTGV regularization, which has been successfully employed for dynamic MRI in [5], for the reconstruction of undersampled qMRI data. ICTGV improves upon spatio-temporal total variation (TV) or global low-rank/sparse regularization due to automatic and local balancing of lower and higher requirements for temporal regularization via infimal convolution5. In this work, the approach was applied together with different sampling strategies and acceleration factors for T1 determination using the variable-flip-angle (VFA) method6,7 and T2 quantification from multi-echo-spin-echo (MESE) data.

METHODS

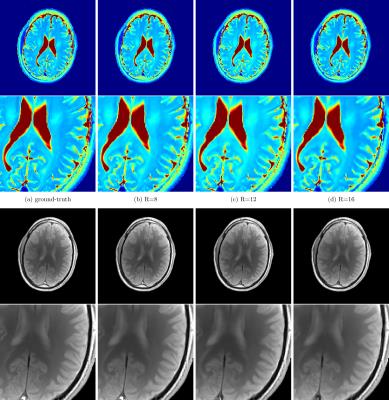
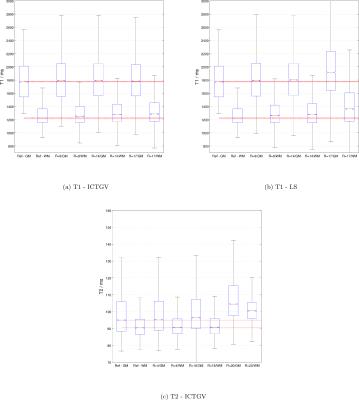
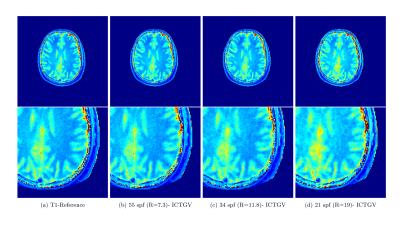
High-resolution Cartesian VFA data of the full brain (256x256x30) and radial VIBE data with golden-angle acquisition8 was acquired with 10 flip-angles $$$ ( \alpha \in \{1,3,5,7,9,11,13,15,17,19\} ° ) $$$ similar to [1] (see Figure 1 and Figure 4, for sequence parameters). The data was acquired on a clinical 3T system from different volunteers. In order to enable rapid slice-by-slice reconstruction a Fourier-transform along the second phase-encoding direction was employed. To study the acceleration potential, the fully-sampled data was retrospectively undersampled with variable-density Poisson-disk sampling (BART toolbox)12 $$$ ( R \in \{ 9,14,17 \} )$$$ for the 3D acquisition and a reduced number of projections for the radial data (55, 34 and 21 spokes-per-frame (spf)). The image series was then recovered from the subsampled Cartesian and non-Cartesian data, employing the ICTGV implementation within the AVIONIC framework (https://github.com/IMTtugraz/AVIONIC) with automatic estimation of coil-sensitivity information. T1 and M0 parameter maps were estimated conventionally by fitting a linearized version of the FLASH signal equation, including a flip-angle correction with Bloch-Siegert mapping9. A similar procedure was carried out for the T2-weighted MESE data (256x256x9), where 30 echoes (TE1=11ms, echo-spacing ΔTE=11ms) were acquired. Here, subsampling was performed retrospectively $$$ (R \in \{4,8,12,16\})$$$ with the VISTA10 strategy to account for the slice-by-slice acquisition. T2 estimation was carried out by fitting a mono-exponential model and skipping the first echo. For both methods quantitative analysis was performed based on gray- and white matter segmentation with the SPM toolbox.

RESULTS

Figure 1 and 2 show the estimated T1 and T2 / M0 estimates for the two different qMRI acquisitions and acceleration factors. In Figure 1, a comparison to a low-rank/sparse regularization11 is shown for the VFA method. A quantitative evaluation is presented in Figure 3 for both methods (T1 and T2 values only) by means of boxplots for the segmented GM and WM regions. Figure 4 shows preliminary results for the VFA data acquired with the golden-angle radial sampling for reduced number of radial views.

DISCUSSION AND CONCLUSION

For both investigated qMRI applications the reconstruction quality of the parameter maps remains stable and in high accordance with the fully-sampled reference up to high acceleration factors. Anatomical details are depicted sharply. This is also reflected by the quantitative, statistical analysis of the histogram of WM and GM. ICTGV achieves better performance than a low-rank/sparse regularization for high acceleration factors. For the VFA method, more residual noise is introduced compared to the MESE method, which results from the higher number of parameter encodings possible for MESE (32 echoes vs 10 flip-angles). These can be acquired without additional scan time for a fixed number of slices. In the current work, the VFA method has been simplified to slice-by-slice processing, but could also be processed as 3D-parameter dataset to explore additional redundancies (with increased computational effort). In comparison to model-based reconstruction the proposed approach does not restrict the reconstruction to a specific signal-model (e.g. mono-exponential). The signal model used for the actual quantification can then be adjusted in dependency of the investigated data after the reconstruction. In summary, ICTGV regularization, originally developed for dynamic MRI data, can be successfully applied to accelerate MR parameter mapping with very high acceleration factors.

Acknowledgements

BioTechMed-Graz, Graz, Austria

Funded by the Austrian Science Fund (FWF) SFB-F3209-18

NVIDIA Corporation Hardware grant support


References

1.Velikina JV, Alexander AL, Samsonov AA "Accelerating MR Parameter Mapping using Sparsity promoting regularization in parametric dimension." MRM 2013; 70(5):1263-73

2. Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang ZP "Accelerated MR Parameter Mapping with Low-Rank and Sparsity Constraints." MRM 2015; 72(2):489-498

3. Block KT, Uecker M, Frahm J "Model-Based Iterative Reconstruction for Radial Fast Spin-Echo MRI." IEEE Trans. Med. Imag. 2009; 28(11)

4. Sumpf TJ, Uecker M, Boretius S, Frahm J "Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo." Magn Reson Imag 2011; 34(2):420–428

5. Schloegl M, Holler M, Schwarzl A, Bredies K, Stollberger R "Infimal Convolution of Total Generalized Variation Functionals for dynamic MRI." MRM 2016; doi:10.1002/mrm.26352

6. Homer J, Beevers MS "Driver-equilibrium single-pulse observation of T1 relaxation. A re-evaluation of a rapid “new” method for determining NMR spin-lattice relaxation times." J Magn Reson 1985; 63: 287-297.

7. Deoni SC, Rutt BK, and Peters TM "Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state." MRM 2003; 49: 515-526.

8. Block KT, Chandarana H, Fatterpekar G, et al. "Improving the Robustness of Clinical T1-Weighted MRI Using Radial VIBE." MAGNETOM Flash 2013; 5:6-11

9. Sacolick LI, Wiesinger F, Hancu I, Vogel MW "B1 mapping by Bloch-Siegert shift." MRM 2010; 63:1315-22

10. Ahmad R, Xue H., Giri, S, Ding Y, Craft J, Simonetti OP "Variable Density Incoherent Spatiotemporal Acquisition (VISTA) for Highly Accelerated Cardiac MRI" MRM 2015; 74(5):1266-1278

11. Otazo R, Candes E, Sodickson DK "Low-Rank Plus Sparse Matrix Decomposition for Accelerated Dynamic MRI with Separation of Background and Dynamic Components." MRM 2015; 73(3):1125-1136

12. Uecker M, Ong F, Tamir JI et al. "Berkeley Advanced Reconstruction Toolbox.", In Proc. Intl. Soc. Mag. Reson. Med. 23 2015;2486


Figures

Figure 1: Comparison of T1 maps computed from the fully sampled VFA flip-angle dataset (TR/TE=5.31/2.46ms, $$$\alpha \in \{1,3,5,7,9,11,13,15,17,19\}$$$ °, 1x1x3mm³) with T1 maps computed from reconstructed subsampled data $$$(R=9,14,17)$$$ using ICTGV regularization (1st and 2nd row (closeup) and a low-rank/sparse regularization (3rd row)

Figure 2: Comparison of T2 and M0 maps computed (1st echo neglected) from the fully sampled MESE dataset (TR/TE1 = 3110/11 ms, ΔTE=11ms, 1x1x5mm³) with T2 and M0 maps computed from subsampled data $$$(R=8,12,16)$$$ with ICTGV regularization.

Figure 3: Statistical analysis of the distribution of T1 (VFA method) and T2 (MESE method) values within a gray (GM) and white matter (WM) segmented region-of-interest for different subsampling factors reconstructed with ICTGV (a,c) and a low-rank/sparse (b) regularization.

Figure 4: T1 maps gained from the ICTGV reconstructed subsampled VFA flip-angle radial VIBE dataset with golden angle acquisition (TR/TE = 4.51/2.11 ms, $$$ \alpha \in \{1,3,5,7,9,11,13,15,17,19 \}$$$°, 1.1x1.1x3mm³) for (spf=55, 34, 21) spokes-per-frame, which corresponds to accelerations of (R=7.3, 11.8, 19).

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3873