3870

Parallel Imaging Reconstruction with Compressed Sensing Calibration for Real-time Neonatal Chest MRI
Yu Y. Li1,2

1Cardiac Diagnostic Imaging, St. Francis Hospital, Roslyn, NY, United States, 2Radiology, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States

Synopsis

In the presented work, a compressed sensing approach is introduced to calibrate k-t space parallel imaging reconstruction. This approach removes the need for calibration data and improves image reconstruction using data sparsity associated with narrow bandwidth of physiological motion signals. The new approach is used to enable real-time neonatal chest MRI. It is experimentally demonstrated that real-time imaging can provide high-quality cardiac and pulmonary images for improved clinical diagnosis in premature babies.

Purpose

MRI provides a safe and information-rich tool for diagnosing pulmonary and cardiac diseases that have been the leading causes of morbidity and mortality in premature babies. Neonatal chest MRI, however, is limited by imaging speed because available techniques lack the ability to track physiological motion in neonates who have smaller anatomy and higher heart/respiration rates than adults. The presented work aims to overcome this challenge with real-time imaging. Here a correlation imaging model 1,2 is used to convert parallel imaging reconstruction into the estimate of correlation functions. A compressed sensing method is used to estimate correlation functions for parallel imaging reconstruction. The new approach is demonstrated in functional and structural MRI examination of the neonatal chest.

Methods

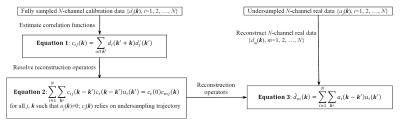
Figure 1 illustrates a correlation imaging model 1,2. In correlation imaging, correlation functions may be estimated from a set of fully-sampled calibration data, e.g., auto-calibration signals (ACS). This may lead to a method equivalent to either GRAPPA or SENSE that has been found insufficient for real-time imaging. The presented work introduces a compressed sensing approach to estimating correlation functions. This can remove the need for calibration data and improve image reconstruction using data correlation associated with data sparsity. As a result, a gain in imaging acceleration can be achieved, making it possible to collect real-time neonatal chest MRI data. The proposed approach is formulated as follows:

Minimize || Ps (x) - y ||

Subject to 1). Reconstructed data x satisfies correlation imaging model in Figure 1; and 2). Correlation functions have sparsity in time,

where Ps represents data undersampling in k-space and y represents the collected data. The image reconstruction is implemented iteratively. Every iteration includes two steps:

Step 1: Correlation functions are calculated from all available data (collected and reconstructed) in k-t space as in Figure 1. The estimated correlation functions are transformed to Fourier space. The sparsity constraint is applied by setting the Fourier spectra to be zeroes outside of the frequency range of cardiac and respiratory motion signals. The modified Fourier spectral are then transformed to the original space by inverse Fourier transform and used as the final correlation functions.

Step 2: The linear equations are formed from the estimated correlation functions and used to resolve the reconstruction operators for image reconstruction from the collected data as in Figure 1. The reconstructed data are modified by data fidelity constraint, i.e., they are equal to the collected data at the sampling k-t space positions. The modified data are used to estimate correlation functions for the next iteration.

To demonstrate real-time neonatal chest MRI, 5 neonatal volunteers (2 weeks to 2 months of age and <2.5kg of weight) were scanned with free-breathing and without sedation. Cardiac CINE imaging data were collected in real-time for ~25 seconds with a temporal resolution of 48 milliseconds (FOV 16cm, matrix 128×128, TR/TE 3.7/1.1 ms, slice thickness 5 mm, flip angle 45°). A set of data collected with k-space segmentation (8 phase encoding lines per segment) was used as references. Real-time lung images were collected for ~40 seconds with a temporal resolution of 123 milliseconds (FOV 16cm, matrix 192×192, slice thickness 6mm, flip angle 10°). A set of static lung images collected with a 3D fast gradient echo sequence with the same acquisition parameters was used as references.

Results

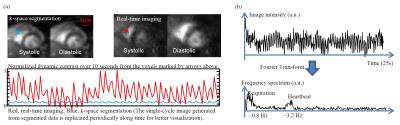
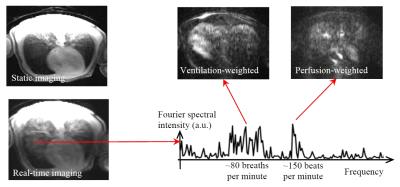
Figure 2 shows a cardiac imaging result with a heart rate of >150 beats per minute. Compared with k-space segmentation, real-time imaging gives better dynamic contrast. The temporal trajectory demonstrates that real-time imaging provides sufficient speed for tracking respiratory and cardiac motion. Figure 3 shows a lung imaging result with a respiratory rate of ~80 breaths per minute. Compared with static imaging, real-time imaging gives higher signal intensity in lung parenchyma. Using the Fourier decomposition approach described in a previous work 3, ventilation-weighted and perfusion-weighted images can be generated.

Discussion

Respiratory or cardiac motion is a narrow-band signal along time and thus sparse in frequency domain. A few center k-space lines (4 in the presented work) can be collected over all the time frames for estimating the frequency bandwidth of respiratory and cardiac motion (Figures 2b). The estimated frequency sparsity is used to improve the estimate of correlation functions for k-t space parallel imaging reconstruction.

Conclusion

The new parallel imaging approach with compressed sensing calibration enables real-time chest imaging for clinical diagnosis of cardiac and pulmonary diseases in premature babies.

Acknowledgements

This work is supported by NIH/NICHD R21HD071540 and NIH R01EB022405.

References

1. Li, Y et al., MRM 2012, 68:2005-2017.

2. Li, Y et al., MRM 2015, 74(6): 1574-1586.

3. Bauman, G et al., MRM 2009, 62: 656-664.

Figures

Figure 1. Correlation imaging model 1,2 gives a mathematical description for general parallel imaging. The model may generate either SENSE-like or a GRAPPA-like reconstruction depending on how correlation functions are estimated.

Figure 2. (a) Real-time cardiac imaging provides better dynamic contrast between systolic and diastolic phases than k-space segmentation. The temporal trajectory plot also shows that real-time imaging gives a higher speed than cardiac (fast wave) and respiratory (slow wave) motion. (b) The Fourier transform of the collected center k-space lines show that the data are sparse in Fourier domain (signals are concentrated within the respiratory and cardiac frequency bands). This frequency sparsity is used to estimate k-t space correlation functions with compressed sensing in correlation imaging model.

Figure 3. Compared with static imaging (upper-left), real-time lung imaging (lower-left) gives higher signals within the lung parenchyma. The Fourier spectrum (lower-right) shows the spectral peaks at the respiratory and cardiac frequencies. They can be used to generate ventilation- and perfusion-weighted images (upper-right) 3. These spectra also demonstrate the frequency sparsity of k-t space data. The frequency sparsity can be used to estimate correlation functions with compressed sensing in correlation imaging model.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
3870