3869
Robust GRASP: A novel approach using the Huber norm in projection space for robust data consistency in undersampled radial MRI1NYU/CUNY/UTFPR, New York, NY, United States, 2Radiology, NYU School of Medicine, New York, NY, United States, 3Computer Science, CUNY, New York, NY, United States
Synopsis
Robust data consistency using the Huber norm is proposed for compressed sensing radial MRI to reduce artifacts associated with outliers in the acquired data that cannot be removed by the sparse reconstruction. System imperfections such as chemical shift can introduce this type of large data distortions, or outliers. The quadratic shape of the usually employed Euclidean norm for data consistency is very sensitive to very large errors. In the proposed method, named RObust Golden-angle Radial Sparse Parallel MRI (ROGRASP), the Huber norm enables large errors to remain in the data discrepancy, not transferring them to the reconstructed image. In vivo acquisitions with outlier-contaminated data illustrate this improvement in quality for free-breathing cardiac MRI.
PURPOSE:
Radial acquisition in combination with compressed sensing, e.g., Golden-angle RAdial Sparse Parallel (GRASP)1 MRI, facilitates rapid continuous dynamic imaging with flexible recovery of temporal information. However, system imperfections, such as chemical shift and off-resonance effects, can result in outliers in the acquired data, which are not properly accounted for in conventional models of data consistency (Euclidean norm). This leads to artifacts in the reconstructed series of images. The Huber norm is known to increase the robustness of algorithms in the presence of outliers2. Therefore, we propose a Huber norm-based data consistency term3 to increase the robustness of GRASP – here applied to cardiac MRI - with respect to artifacts associated with outliers.METHODS:
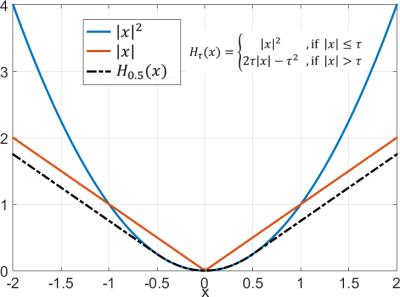
In GRASP, streak artifacts appear as radial lines fluctuating over time frames, usually caused by undersampling. System imperfections, such as chemical shift, misalign measurements of the radial spokes, resulting in large errors known as outliers. These outliers also contribute to the streak artifacts, and they are easily visualized in the projection domain. The Huber norm provides squared magnitudes for small magnitude values, e.g., $$$|x|^2$$$, as in the Euclidean norm, and unsquared magnitudes for large errors, e.g., $$$|x|$$$, like the L1 norm, (Figure 1), so large errors become less relevant. Here, the Huber norm replaces the Euclidean norm, being applied in the projection domain – as in Computed Tomography - instead of k-space. The proposed algorithm, termed RObust GRASP (ROGRASP), is formulated as follows: $$x=\arg \min_x \: \: H_{\tau}(E(m-FSx)) + \lambda||Tx||_1 ,$$ where $$$x$$$ is the image time-series to be reconstructed, $$$S$$$ is the matrix with coil sensitivities for all frames, $$$F$$$ represents the NUFFT operator4 for all coils and frames, $$$H_{\tau}(y)$$$ is the Huber norm with parameter $$$\tau$$$, $$$E$$$ represents a series of 1D FFTs applied to each radial k-space line to transfer data into projection space, and $$$T$$$ is the first-order differences applied along the cardiac motion dimension1, hence, $$$||Tx||_1$$$ reflects temporal total variation (TTV) with $$$\lambda$$$ as the regularization parameter.
Two representative cardiac data sets were utilized for comparison. The datasets were continuously acquired during free-breathing with golden-angle radial sampling (Case 1: 1.9 seconds, 620 spokes, TR = 3.1 ms, 10 coils; Case 2: 1.01 seconds, 405 spokes, TR = 2.5 ms, 12 coils). Consecutive spokes were grouped together to form each temporal frame (Case 1: 20 spokes/frame; Case 2: 15 spokes/frame).
Standard GRASP and the proposed ROGRASP reconstructions were performed. For the latter, a modified FISTA algorithm5 was employed, using the fast gradient projection6 for the proximal operator of the TTV prior. Regularization parameters were adjusted separately for GRASP and ROGRASP, such that temporal sparsity of both methods, measured by $$$||Tx||_1$$$, was nearly the same. The Huber parameter was empirically set to 1e-5, which corresponds to selecting approximately 12.5% of the error elements as outliers. For both, 80 iterations were performed.
RESULTS:
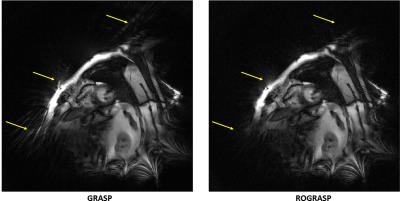
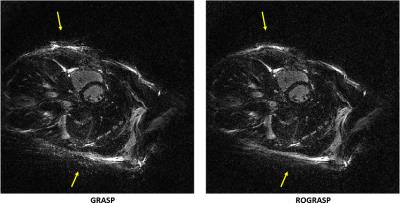
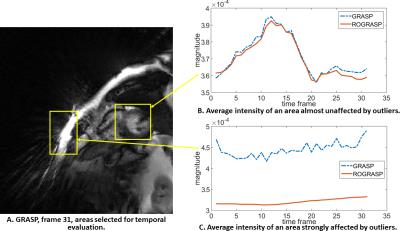
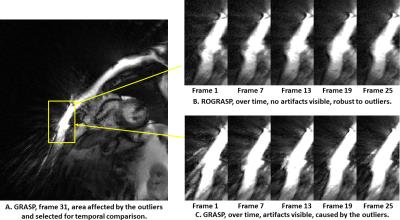
ROGRASP significantly improves areas affected by outlier artifacts, compared to standard GRASP (Figure 2 and 3, yellow arrows). Note that the contrast was amplified to emphasize artifacts in the images. Most streak artifacts originate from regions of strong fat signals, which illustrates how chemical shift effects can cause large errors in the data acquisition7. Figure 4 demonstrates the temporal fidelity of different regions-of-interest. In areas almost unaffected by the outliers (Fig. 4B), the spatially averaged magnitude over time is similar for both methods. However, in outlier-affected areas (Fig. 4C), the same measurement differs significantly. This difference is mainly due to artifacts caused by outliers. Figure 5 reflects how these areas vary over several time frames.DISCUSSION:
Most of the streak artifacts in cardiac
radial MRI are caused by insufficient sampling rate. Using more data, if
possible, or a sparse reconstruction approach, can highly reduce these
artifacts. However, if data are contaminated by outliers, neither more data, nor
sparse reconstruction alone, solves the problem, since these outliers are
consistent with the data according to the usually employed Euclidean norm. The
Huber norm provides a better way to solve this problem, due to its property of
allowing large errors to stay in the data discrepancy residual, not
transferring them to the reconstructed images as artifacts.
CONCLUSION:
The proposed reconstruction method was able to deal better with outliers in the data, especially when a Euclidean norm failed to ensure good results. There can be many sources of large errors, such as suboptimal estimation of coil sensitivities or chemical shift and off-resonance effects from fat7. We believe that not only cardiac MRI, but also many other MRI reconstruction problems, may be improved with this new robust compressed sensing algorithm.Acknowledgements
This research was partially supported by NIH grant P41 EB017183.References
1. L. Feng, R. Grimm, K. T. Block, H. Chandarana, S. Kim, J. Xu, L. Axel, D. K. Sodickson, and R. Otazo, “Golden-Angle Radial Sparse Parallel MRI: Combination of Compressed Sensing, Parallel Imaging, and Golden-Angle Radial Sampling for Fast and Flexible Dynamic Volumetric MRI,” Magn. Reson. Med., vol. 72, no. 3, pp. 707–717, Sep. 2014.
2. J. A. Scales and A. Gersztenkorn, “Robust Methods in Inverse Theory,” Inverse Probl., vol. 4, no. 4, pp. 1071–1091, Oct. 1988.
3. A. Guitton and W. W. Symes, “Robust Inversion of Seismic Data Using the Huber Norm,” Geophysics, vol. 68, no. 4, pp. 1310–1319, 2003.
4. J. A. Fessler and B. P. Sutton, “Nonuniform Fast Fourier Transforms Using Min-Max Interpolation,” IEEE Trans. Signal Process., vol. 51, no. 2, pp. 560–574, Feb. 2003.
5. D.-S. Pham and S. Venkatesh, “Efficient Algorithms for Robust Recovery of Images From Compressed Data,” IEEE Trans. Image Process., vol. 22, no. 12, pp. 4724–4737, Dec. 2013.
6. A. Beck and M. Teboulle, “Fast Gradient-Based Algorithms for Constrained Total Variation Image Denoising and Deblurring Problems.,” IEEE Trans. Image Process., vol. 18, no. 11, pp. 2419–34, Nov. 2009.
7. T. Benkert, L. Feng, D. K. Sodickson, H. Chandarana, and K. T. Block, “Free-Breathing Volumetric Fat/Water Separation by Combining Radial Sampling, Compressed Sensing, and Parallel Imaging,” Magn. Reson. Med., pp. 1–28, Sep. 2016.
Figures