Synopsis

In this work a joint cardio-respiratory motion estimation technique is introduced for the compensation of both the respiratory and cardiac motion of the heart during free-breathing cardiac MRI examinations. The proposed technique is combined with an extra-dimensional reconstruction scheme in which respiratory and cardiac motions are resolved. Initial results for 2D cine cardiac MRI are presented for synthetic and real data.

Introduction

Respiratory motion is still an issue in MRI of the heart despite the introduction of Compressed Sensing (CS) techniques$$$^1$$$, which significantly reduce the time needed for acquisition. Recently, an eXtra-Dimensional (XD) scheme has been proposed (XD-GRASP)$$$^2$$$­­ which sorts k-space data according to both the respiratory and the cardiac phases at which they were were acquired. This way, cardiac and respiratory motions are separated and resolved in the final images. At reconstruction, temporal total variation (tTV) along the two pseudo-temporal dimensions defined (respiratory and cardiac phases) is used as sparse domain. Additional spatial TV regularization has been introduced. The following optimization problem results:

$$\underset{\mathbf{m}}{\mathrm{minimize}} \frac{1}{2}\|\mathbf{y}-\mathbf{Em}\|_2^2 + \lambda \| \nabla_{RC} \mathbf{m}\|_1 + \lambda_s \|\nabla_{xy} \mathbf{m}\|_1$$

where $$$\mathbf{y}$$$ is the acquired k-space data, $$$\mathbf{E}$$$ the encoding operator (comprising coils sensitivities multiplication and undersampled non-uniform Fourier transform) and $$$\nabla_{RC}$$$ stands for the temporal finite differences operator along both respiratory and cardiac pseudo-temporal dimensions.

However, in this approach large motion between different cardio-respiratory states leads to a reduction of the sparsity of the signal after the application of $$$\nabla_{RC}$$$. CS based reconstruction methods have been successfully combined with motion compensation (MC) techniques either to correct for the respiratory motion$$$^3$$$ or to estimate the heart beat motion to foster the sparsity of the dynamic data, hence improving the quality of the reconstructed images$$$^4$$$. These methods have shown to enable higher acceleration factors than standard CS methods or alternatively, for a given acceleration factor, to give rise to better images.

In this work, we propose a MC technique to jointly estimate the respiratory and cardiac motions of the heart and we introduce it in a XD reconstruction scheme, enabling the MC-CS reconstruction of respiratory resolved cardiac MRI. We show initial results for the reconstruction of 2D free-breathing cardiac cine MRI, on both synthetic and real data.

Methods

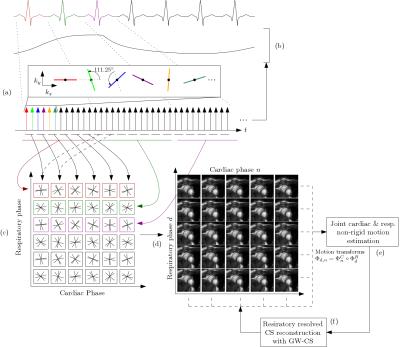
The general procedure is summarized in Figure 1. Data is continuously acquired following a Golden Radial trajectory and ECG is recorded for synchronization.

i) Motion estimation: We model the cardio-respiratory motion as the composition of two independent spatial deformations, $$$\Phi_{r,c}^{R,C} = \Phi_{r}^{R} \circ \Phi_{c}^{C}$$$ , where $$$\Phi_{r}^{R}$$$ describes the respiratory deformation and $$$\Phi_{c}^{C}$$$ the cardiac motion. Both models are based on free-form deformations and a groupwise registration procedure$$$^4$$$. In a first step data from each cardiac cycle is merged together. A low temporal resolution sequence results from both the respiratory signal and $$$\Phi_{r}^{R}$$$ are estimated. In a second step, the XD scheme is applied and cardiac motion is estimated jointly from all the images at different respiratory states.

ii) MC-CS XD reconstruction: By composing $$$\Phi_{r}^{R}$$$ and $$$\Phi_{c}^{C}$$$ we define the MC operator $$$\Phi_{r,c}^{R,C} $$$ that, when applied to the dynamic image $$$\mathbf{m}$$$, deforms it to a common cardio-respiratory configuration.We introduce it in the sparsity regularization term of the XD-CS reconstruction problem and solve:

$$\underset{\mathbf{m}}{\mathrm{minimize}} \frac{1}{2}\|\mathbf{y}-\mathbf{Em}\|_2^2 + \lambda \| \nabla_{RC}\Phi_{r,c}^{R,C}\mathbf{m}\|_1 + \lambda_s \|\nabla_{xy} \mathbf{m}\|_1$$

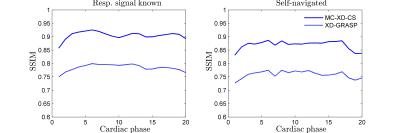
iii) Experiments: We first use synthetic data generated with the numerical phantom XCAT$$$^5$$$. This way, a ground truth is available and the structure similarity index (SSIM) is calculated for quantitative validation. In order to study the sensitivity of the proposed method to errors in the respiratory synchronization, we reconstruct the simulated data using the respiratory signal provided by XCAT and the one estimated from the data.

Secondly, a healthy volunteer was scanned with a 32-element cardiac coil and the described trajectory on a 1.5T Philips scanner during 14 seconds. Other relevant scan parameters include TR/TE/$$$\alpha$$$ = 2.9ms/1.44ms/60$$$^\circ$$$, FOV = 320x320mm$$$^2$$$, spatial resolution of 2x2mm$$$^2$$$. Reconstructed images are shown for visual quality assessment.

Results and discussion

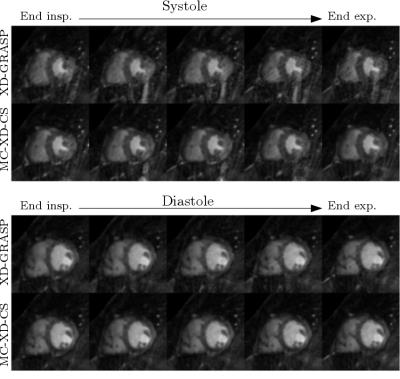
In Figure 2 the results obtained from the synthetic data are shown at four respiratory states for systole and diastole. Sharper edges and better contrast between blood and myocardium can be appreciated in the proposed method when compared with XD-GRASP reconstructions, in which no MC is performed. No significant degradation of the image quality is observed when using the respiratory signal estimated from the data for self-navigation. In Figure 3, the SSIM calculated shows consistent superior performance of the proposed method along the cardiac cycle.

Figure 4 shows the results from the real data at systole (top) and diastole (bottom) for five respiratory states. Less undersampling artifacts and better small papillary muscles delineation are observed when the MC technique is introduced.

Conclusion

To the best of our knowledge, in this work a joint cardio-respiratory non-rigid MC technique has been introduced for the first time in a XD CS reconstruction scheme. The results reported show better performance than the non-MC counterpart and robustness against respiratory synchronization errors.

Acknowledgements

References

1. Lustig, M., Donoho, D. and Pauly, J. M. (2007), Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med., 58: 1182–1195.

2. Feng, L., Axel, L., Chandarana, H., Block, K. T., Sodickson, D. K. and Otazo, R. (2016), XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magn. Reson. Med., 75: 775–788.

3.Usman, M., Atkinson, D., Odille, F., Kolbitsch, C., Vaillant, G., Schaeffter, T., Batchelor, P. G. and Prieto, C. (2013), Motion corrected compressed sensing for free-breathing dynamic cardiac MRI. Magn. Reson. Med., 70: 504–516.

4. Royuela-del-Val, J., Cordero-Grande, L., Simmross-Wattenberg, F., Martín-Fernández, M. and Alberola-López, C. (2016), Nonrigid groupwise registration for motion estimation and compensation in compressed sensing reconstruction of breath-hold cardiac cine MRI. Magn. Reson. Med., 75: 1525–1536.

5. Segars WP, Sturgeon GM, Mendonca S, Grimes J, and Tsui BMW. 4D XCAT Phantom for Multimodality Imaging Research. Medical Physics, vol. 37, pp. 4902-4915, 2010.