3866
True Temporal Resolution TWIST Imaging using Annihilating Filter-based Low-rank wrap around Hankel Matrix1KAIST, Daejeon, Korea, Republic of, 2EPFL, Lausanne, Switzerland, 3Gacheon University Gil Medical Center, Incheon, Korea, Republic of
Synopsis
Temporal resolution is an important factor in dynamic enhanced contrast (DCE) MRI. Time-resolved angiography with interleaved stochastic trajectories (TWIST) has been widely used due to its improved temporal and spatial resolution. However, the temporal resolution of TWIST imaging is not a true one because of the view sharing. To provide more improved temporal resolution, we proposed a novel reconstruction algorithm based annihilating filter-based low rank Hankel matrix approach (ALOHA) which exploits the fundamental duality between sparsity in transform domain and low-rankness of Hankel matrix constructed using k-space data. Experimental result using in-vivo data showed the significantly improved temporal resolution than the conventional reconstruction.
Introduction
TWIST imaging gives improved temporal and spatial resolution1. However, the temporal resolution of TWIST imaging is not a true one, because the periphery of k-space from several frames should be shared to make one image. The purpose of this study is to achieve the true temporal resolution by reducing view sharing significantly. The resulting k-space is sampled irregularly, which cannot be interpolated using GRAPPA. Instead, we employ recent annihilating filter-based low-rank Hankel matrix approach (ALOHA) to interpolate the missing k-space data2. Experimental results using in-vivo data showed significantly improved temporal resolution with comparable spatial resolution.Theory
Suppose that a signal, $$$ x(t) $$$, is one of the finite rate of innovation (FRI) models which can be represented as sum of Diracs. Then, we can find the associated annihilating filters in k-space, $$$ \hat{h}[k] $$$, such that $$$(\hat{h}*\hat{x})[k] = 0, \forall k.$$$ This discrete convolution operation in k-space can be represented as the matrix-vector multiplication: $$ \mathscr{H}({\hat{\mathbf{x}}})\bar{\hat{\mathbf{h}}} = 0, $$ where $$$\mathscr{H}({\hat{\mathbf{x}}})$$$ is the Hankel matrix constructed from $$$\hat{x}[k]$$$ and $$$\bar{\hat{\mathbf{h}}}$$$ denotes the vectorized annihilating filter in k-space. Let $$$r+1$$$ denote the minimum size of annihilating filters. Then, we can show that the rank of the given Hankel matrix is $$$r$$$2. If the reconstruction domain is discrete, this property still holds if we use a wrap-around Hankel matrix $$$ \mathscr{H_c}(\hat{\mathbf{x}})$$$ as illustrated in Fig.2.
The signal in the image domain is not sparse in general, so the signal can be sparsified using wavelet transform. Moreover, the intercoil redundancy can be also exploited in ALOHA. Specifically, we can construct a horizontally concatenated matrix $$$\mathcal{Y}$$$
$$\mathcal{Y} = \left[ \mathscr{H}_c(\hat{\mathbf{x}}_1) \ \cdots \ \mathscr{H}_c(\hat{\mathbf{x}}_{N_c})) \right],$$ which can be shown low-ranked $$$\mathcal{Y}$$$2. In addition, the filter size can be reduced than that of single coil, if we use wrap-around Hankel matrix. In this study, we applied Haar wavelet weighting to $$$k_y-k_z$$$ data to make the signal sparse in wavelet transform domain. Then, the k-space was reconstructed by solving low-rank Hankel matrix completion problem using pyramidal decomposition, which makes algorithm robust to noise boosting.
Method
The 3D DCE data for carotid and cerebral vessel imaging was acquired with a TWIST sequence using Siemens 3T Verio scanners. The sequence parameters are as following : repetition time (TR) 2.73 ms, echo time (TE) 1.08ms , 222$$$\times$$$896$$$\times$$$114 matrix size, 16 coils and 20 temporal frames. $$$24\times 24$$$ ACS regions were used for GRAPPA reconstruction. In addition, only 64% of data was acuqired. The setting number of view sharing for standard GRAPPA reconstruction was five (Fig. 3(a)), whereas we only used two frames for our purpose (Fig. 3(b)).
The reduced view sharing results in the irregular sampling pattern which cannot be reconstructed using conventional compressed sensing (CS)3 because of the severe coherent aliasing artifacts. Therefore, we utilized ALOHA to interpolate the k-space with reduced view sharing. Thanks to wrap-around Hankel matrix, the filter size is reduced. The k-space interpolation problem can be represented as $$ \begin{eqnarray} \min_{\mathcal{Y}}&& \|\mathcal{Y}\|_* \\ \mbox{subject to} &&\mathcal{Y} = \begin{bmatrix} \mathscr{H_c}\{\widehat{\mathbf{Y}}_1\}~\cdots~\mathscr{H_c}\{\widehat{\mathbf{Y}}_C\} \end{bmatrix}, \end{eqnarray} \\ \hat{y}_i(\mathbf{k})=\hat{\phi}(\mathbf{k})\hat{x}_i(\mathbf{k}),\quad \mathbf{k} \in \Omega,$$ where $$$\widehat{\mathbf{Y}}_i$$$ denotes a matrix constructed from discrete samples of $$$\hat{y}_i(\mathbf{k})$$$, and $$$\hat{\phi}(\mathbf{k})$$$ is a wavelet weighting. $$$\hat{x}_i(\mathbf{k})$$$ denotes a k-space measurement from $$$i$$$-th coil, and $$$\Omega$$$ is the index set of measured k-space data. This cost function can be minimized by alternating directional method of multiplier (ADMM) algorithm.
Result
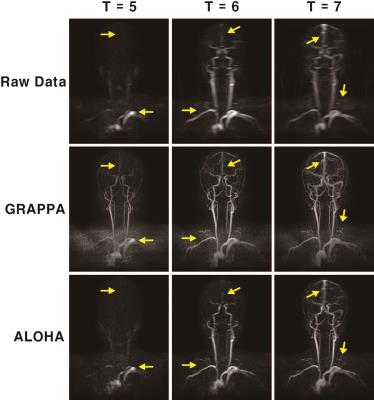
The subtracted MIP images for data are illustrated in Fig.4 . To compare the temporal resolution, we select the images from the 5th frame to the 7th frame which shows the propagation of contrast agent. In ALOHA reconstruction, the contrast agent is spread out more gradually, whereas the sudden jumps of contrast agent can be found in the conventional reconstruction. We also show the low-frequency only reconstruction results in Fig. 4 that has the best temporal resolution. The ALOHA temporal resolution coincided with the low-frequency only reconstruction. Even though only two frames were used to interpolate the k-space data for one image, the spatial resolution in ALOHA reconstruction was comparable to the conventional reconstruction.Discussion and Conclusion
In this paper, to enhance the temporal resolution of TWIST imaging with comparable spatial resolution, we proposed a novel reconstruction algorithm using ALOHA. By using wrap-around Hankel matrix, the computational complexity can be reduced because of the reduced filter size depending on the number of coils. In addition, ALOHA can exploit the sparsity in transform domain and the coil diversity, which is ideal to improve the temporal resolution of TWIST imaging. Therefore, we believe that the proposed method can provide better diagnostic quality due to the improved temporal resolution.Acknowledgements
This study was supported by Korea Science and Engineering Foundation under Grant NRF-2016R1A2B3008104.References
1. Gerhard L and Randall K. syngo TWIST for dynamic time-resolved MR angiography. Magnetom Flash. 2006;34(3):92-95.
2. Kyoung Hwan J, Dong-wook L, and Jong Chul Y. A General Framework for Compressed Sensing and Parallel MRI Using Annihilating Filter Based Low-Rank Hankel Matrix. IEEE Trans. on Computational Imaging. 2016;2(4):480-495.
3. Donoho, David L. Compressed sensing. IEEE Trans. on Information Theory. 2006;52(4): 1289-1306.
Figures