3865

Free-breathing and ungated cardiac imaging using calibrationless manifold smoothness regularization

Sunrita Poddar¹, Xiaoming Bi², Dingxin Wang², and Mathews Jacob¹

¹University of Iowa, Iowa City, IA, United States, ²Siemens Healthcare

Synopsis

We introduce an image manifold smoothness regularization, coupled with spatial regularization, for high-resolution free-breathing and ungated cardiac cine imaging. Prior work in this area relied on additional navigators within each image frame to estimate the manifold structure. In this abstract, we focus on eliminating the need for navigators, which will provide improved sampling efficiency.

Purpose

Functional cardiac CINE imaging is often performed with breath-holds to freeze cardiac motion. This is infeasible for many patients who cannot perform breath-holding. The breath-held protocol with intermittent pauses also results in long scan-time and restricts patient throughput. While single-shot schemes can be used, the achievable spatial/temporal resolution is limited. Thus, there is an urgent clinical need for a free breathing ungated cardiac CINE protocol.

Method

We extend the image manifold smoothness regularization (STORM)¹ scheme, where the similarity of images at the same cardiac/respiratory phases was exploited. STORM was enabled by a modified golden angle acquisition, where 3-4 spokes are acquired at the same k-space locations every frame. The measurement for the $$$i^{th}$$$ image frame is specified by $$\underbrace{\begin{bmatrix}\mathbf z_i\\ \mathbf y_i\end{bmatrix} }_{\mathbf b_i}= \underbrace{\begin{bmatrix}\mathbf \Phi\\ \mathbf B_i\end{bmatrix} }_{\mathbf A_i} \mathbf x_i + \mathbf n_i$$ where $$$\mathbf z_i$$$ denotes the navigator measurements. $$$\mathbf y_i$$$ are the measurements that are different every frame. The Laplacian of the image manifold $$$\mathbf L$$$ is estimated from navigator data ($$$\mathbf Z = \mathbf \Phi\mathbf X$$$) as $$$\mathbf L = \mathbf D-\mathbf W$$$, where$$\mathbf W_{i,j} = \exp\left(-{\| \mathbf z_i - \mathbf z_j\|^2}/{\sigma^{2}}\right);~~~ \mathbf D = {\rm diag}(\mathbf 1^T \mathbf W)$$While STORM exploits the non-local similarities between images in the time series, it fails to capture the redundancies within each image. We improve STORM by adding a spatial total variation prior:$$\mathbf X^* = \arg\min_{\mathbf X} \left\lbrace \|\mathcal{A}(\mathbf X) - \mathbf b\|_F^2 + \lambda_1~{\rm trace}\left(\mathbf X \mathbf L \mathbf X^{H} \right) + \lambda_2 ~\|\mathbf T \mathbf X \|_{\ell_1}\right\rbrace$$Here, $$$\mathbf T$$$ is the spatial gradient matrix. We use FISTA² to solve the above optimization scheme.

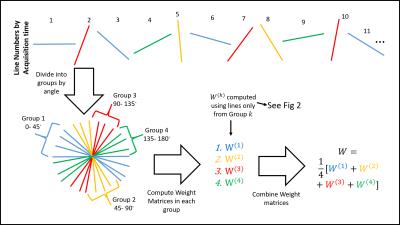
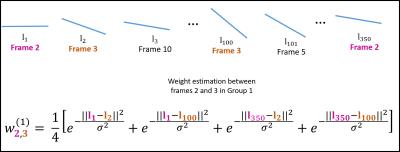
We now introduce a technique (illustrated in Fig. 1) to estimate the weight matrix $$$\mathbf W$$$, when navigators are not available. We split the radial spokes in the entire golden angle acquisition to $$$K$$$ groups, denoted by $$$G_k$$$, each of size $$$180/K$$$ degrees. We evaluate approximate weight matrices $$$\mathbf W^{(k)};k=1,..,K$$$ by comparing spokes in the images that are in the $$$k^{\rm th}$$$ group (Fig. 2):$$\mathbf W_{i,j}^{(k)} = \frac{1}{N_{ij}^k}\sum_{\{\mathbf l_m^{(i)},\mathbf l_n^{(j)} \in G_k\}}\exp\left(-{\|\mathbf l_m^{(i)} - \mathbf l_n^{(j)}\|^2}/{\sigma^{2}}\right)$$Here, $$$\mathbf l_m^{(i)}$$$ and $$$\mathbf l_n^{(j)}$$$ are spokes in the $$$i^{\rm th}$$$ and $$$j^{\rm th}$$$ image frames, which are in group $$$G_k$$$. $$$N_{i,j}^k$$$ denotes total number of spoke pairs in $$$k^{\rm th}$$$ group between frames $$$i$$$ and $$$j$$$. If there is no pair of spokes between two image frames, the corresponding weight is set to zero. The complete weight matrix is calculated as $$\mathbf W = \frac{1}{N} \sum_{k=1}^{N} \mathbf W^{(k)}$$To prevent over-smoothing, $$$\mathbf W$$$ is post-processed to keep only 3-5 neighbours per frame.

Results

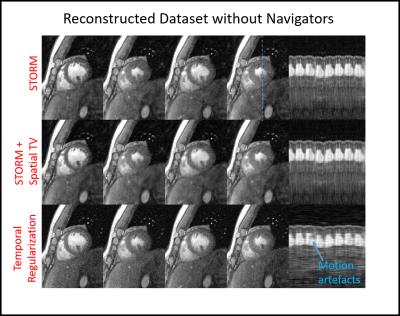
We demonstrate our scheme on two free-breathing ungated cardiac datasets, acquired using a FLASH sequence on a 3T scanner (MAGNETOM Skyra, Siemens Healthcare, Germany). Both datasets were reconstructed using the STORM-TV reconstruction algorithm. The first dataset had 10 radial spokes per frame, out of which 4 were navigator spokes. The sequence parameters were: TR/TE 4.3/1.92 ms, FOV 300mm, Base resolution 256, Bandwidth 574 Hz/pix. 10000 spokes of k-space were collected in 43 s. Fig. 3 shows a few reconstructed image frames, where the weights were computed using navigator spokes. The second dataset was acquired with a golden angle ordering (no navigators). The sequence parameters were: TR/TE 3.7/1.67 ms, FOV 300mm, Base resolution 256, Bandwidth 977 Hz/pix. 11994 spokes of k-space were acquired in 44s and we used 13 spokes to reconstruct each image frame. The spokes were divided into 20 angle groups. Fig. 4 shows a few reconstructed image frames using the proposed scheme. We also show a reconstruction when only the temporal neighbours of each frame are assigned non-zero weights equal to 1.

Discussion

We observe that the spatial TV prior, which is complementary to the STORM prior, reduces noise and streaking artefacts. Our experiments in Fig. 4 using temporal regularization alone results in excessive motion blurring, manifested as long streaks in the time profiles. The comparisons of Fig. 3 and Fig. 4 show that the image quality obtained with the navigator data in Fig. 3 is superior to the calibrationless setting in Fig. 4. We plan to investigate more sophisticated kernel completion methods³ to improve the weight evaluation in the calibrationless setting.

Conclusion

Spatial regularization is complementary to image manifold regularization which exploits the non-local similarities between image frames in a time series. The combination of the priors provides improved results. The heuristic approach to estimating the weights from calibrationless data shows promise; more work is required to improve the estimation of the manifold structure in cases without navigators.

Acknowledgements

No acknowledgement found.

References

1. S. Poddar, M. Jacob, "Dynamic MRI using Smoothness Regularization on Manifolds (SToRM)", IEEE Transactions on Medical Imaging, Vol 35, No 4, April 2016.

2. A. Beck, M. Teboulle, "Fast Gradient-based algorithms for Constrained Total Variation Image Denoising and Deblurring Problems", IEEE Transactions on Image Processing, Vol 18, No 11, Nov 2009.

3. S. Bhadra, S. Kaski, J. Rousu, "Multi-view Kernel Completion", arXiv:1602.02518.

IEEE Trans. Image Proc. vol. 18, no. 11, November 2009, 2419

arXiv:1602.02518

Figures

Fig 1. Summary of weight estimation without navigators: The sequence of radial lines are shown arranged by the order in which they were acquired. The lines are now grouped according to their angle. Here 4 groups have been illustrated. Weight matrices are estimated for each group. These are then averaged to form the final weight matrices.

Fig 2. Group-wise weight estimation: As an example it is illustrated how the weight matrix for group 1 is estimated. The lines are shown is blue as they come from group 1 of Fig 1. In order to compute the weight between frames 2 and 3 for group 1, we require lines 1 and 350 (from frame 2) and 2 and 100 (from frame 3).

Fig 3. Reconstructions using navigators: The top row shows reconstructed images using the STORM algorithm, where the weights were computed using the navigator lines. The bottom row shows reconstructed images with STORM and spatial TV regularization. The temporal profiles along the dotted blue line are also shown for both the reconstructed datasets.

Fig 4. Reconstructions without navigators: Row 1 shows reconstructed images using the STORM algorithm, where the weights were computed using the proposed method. Row 2 shows reconstructed images with STORM and spatial TV regularization. Row 3 shows reconstructed images when only the temporal neighbours of each frame are assigned non-zero weights. This purely temporal regularization scheme results in noisy images as well as excessive motion blurring, as seen from the temporal profiles. This motivates the need for choosing the neighbours carefully. The temporal profiles along the dotted blue line are shown for all the reconstructed datasets.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

3865