Purpose

T2 mapping is an important method for quantitative characterization of tissues. Conventional techniques based on spin-echo or fast spin-echo (FSE) sequences require long acquisition times in order to generate images at multiple echo times (TE) which are subsequently used for T2 fitting. Radial FSE methods have been shown to provide accurate T2 maps from highly undersampled data [2,3]. These techniques combine accelerated radial data acquisition with reconstruction methods using (global) subspace constraints obtained via Principal Component Analysis (PCA) along the TE dimension. The selection of the model order K (i.e., number of principal components (PCs)) used during reconstruction involves a trade-off between model error and noise amplification [4]. In this work, we introduce a T2 mapping technique based on non-local clustering of signal relaxation curves which provides reduced model error and leads to increased acceleration.

Technique

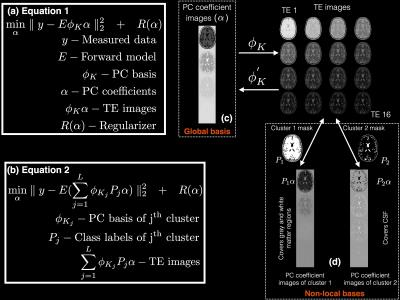
Subspace constrained T2 mapping methods estimate the temporal (contrast) subspace either from acquired training data [5] or from training curves generated from a signal model [1-4]. Huang et al. [3] proposed to use the Slice resolved Extended Phase Graph (SEPG) formulation [6] for the signal model since this model accounts for indirect echoes caused by non-180^o refocusing pulses. Given T1, T2, B1 field, and the profiles of the excitation and refocusing RF pulses, the SEPG model can provide the signal decay curve. Sweeping over the expected range of parameter values, a set of training curves are obtained. These curves are then used to generate a PC basis. Since most of the variation in the training curves can be explained by a small number of PCs, the signal can be constrained to lie in a lower dimensional subspace by truncating the PC basis to keep only the most significant K PCs. Given the truncated PC basis φ_K, the reconstruction problem was formulated as shown in Figure 1(a) in [3,4]. Here, the data consistency term incorporates the temporal subspace constraint due to the use of the truncated PC basis φ_K. Furthermore, a single global PC basis that accounts for the variations in the entire image was used as illustrated in Figure 1(c). In contrast, our proposed approach is shown in Figs. 1(b) and 1(d). The basic principle behind our approach is that if the pixels can be divided into clusters with similar temporal behavior, a separate truncated PC basis can be obtained for each cluster, resulting in a more efficient representation of the temporal characteristics of every pixel. The cluster membership can be determined using a first pass reconstruction followed by k-means clustering.

Methods

Simulations were performed to compare the model errors associated with truncated global and non-local bases for typical T2 and B1 values. The digital phantom experiments, based on the numerical phantom developed by Guerquin-Kern [7], were also carried out to simulate a radial FSE brain dataset with representative T1, T2, and B1 values of brain tissues, ETL=16, and SNR=35dB at the first TE. For the in-vivo experiments, data was acquired on a Siemens 3T Skyra scanner using a radial fast spin echo sequence with echo spacing=8.78ms, ETL=16, TR=4000ms, slice thickness=5mm, 256 radial views/TE, 256 readout points. The data was retrospectively undersampled to 16 radial views/TE to simulate acceleration. SEPG training curves were generated based on the excite and refocusing slice profiles that were used in the pulse sequence. K=4 was used in the in vivo results for the global method. Two clusters with K1=3, K2=3 were used for the non-local method.

Results and Discussion

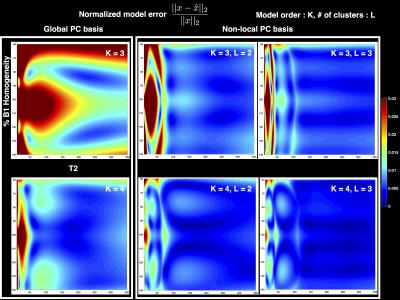
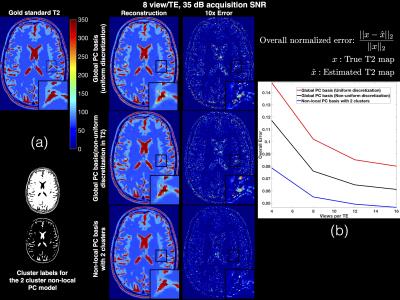
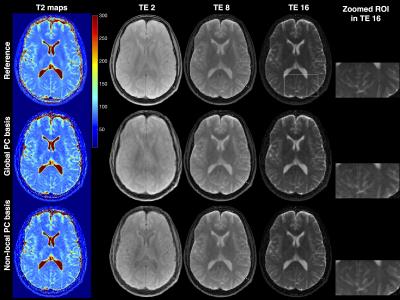
Figure 2 shows the normalized model error in the global and non-local PC bases when using 2 and 3 clusters. It can be seen that the clustering in the non-local PC bases leads to significantly reduced model error. Results of the digital phantom simulations are presented in Figure 3(a). It can be seen that the proposed method with non-local PC bases provides substantial reduction of undersampling artifacts in the T2 maps. Figure 3(b) illustrates the overall normalized error for different methods at various acceleration rates (views/TE). This plot suggests that the proposed method could provide an additional factor of 4 increase in acceleration rate in comparison to earlier methods. Figure 4 illustrates an in vivo comparison of different methods. While some of the details are washed out in the TE images obtained by the global PC basis, the proposed non-local method preserves these details.

Conclusions

A method which uses non-local clustering and multiple PC bases to improve on (global) subspace constrained T2 mapping was proposed. The results show that the proposed method can provide increased acceleration in radial FSE T2 mapping applications.

Acknowledgements

SM acknowledges support from the TRIF Imaging fellowship and TRIF SEOS fellowship.