3862
Fast 4D MRI Reconstruction Analytics using Low-Rank Tensor Imputation1Stanford University, Stanford, CA, United States, 2Stanford University, United States
Synopsis
An imaging analytic is proposed that efficiently reconstruct high-resolution 4D MR images using GPU computing. Modeling k-space data low dimensionality with low PARAFAC rank of tensors, the correlation across different dimensions are captured via tensor subspaces, sequentially learned from the subsampled data, to impute the missing k-space entries. The novel analytics gain considerable computational saving relative to the state-of-the-art compressive sampling schemes, while achieving failry similar image quality.
Introduction
MRI is a major imaging modality for diagnostic and therapeutic guidance in clinics. The need for high-resolution 4D images and dynamic deformation of organs highly slow down the acquisition. This “curse of dimensionality” also burdens the computational and storage units to run nowadays reconstruction analytics such as non-smooth compressive sampling (CS) methods [1]. To accelerate both acquisition and computations, this study advocates a novel tensor subspace learning (TSL) scheme that permeate benefits from PARAFAC decomposition of tensors to low-rank modeling of k-space data. This scheme is applied to 4D MRI with three spatial dimensions plus an additional cardiac dimension. Collecting k-space data over coils and time in a 5D array, the latent correlation across various dimensions is captured by means of a tensor low-rank surrogate. Adopting stochastic alternating-minimization, a sequential algorithm is devised that involves highly parallelizable tasks well suiting GPU implementation.Methods
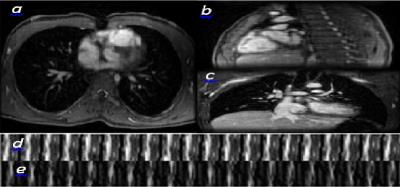
Imaging. A GE MR750 3T-scanner is used with C=32 coils. The sequence consisted of unbalanced minimum TE flow-encoding gradients in a cardiac synchronized 3D Cartesian RF-spoiled gradient echo sequence. Parameters include flip angle 15o, TE=1.8msec, TR=3.9msec with 5.1msec for a standard fat-saturation pulse, and bandwidth of ±83.33kHZ. A velocity encoding range of 250cm/s was used to avoid velocity aliasing in the aortic and pulmonary flows. Scans performed after injection of 0.1mL/kg ferumoxytol for blood pool enhancement. Cartesian sampling with variable-density sampling and radial view-ordering is performed (14.8mins) to image T=20 frames of dimensions M=N=224, P=120.
Reconstruction approach. Consider a 3D image stream $$$\{\underline{\mathbf{X}}_t\}_{t=1}^T \in \mathbb{C}^{M \times N \times P} $$$ acquired across C coils and T time instants. The k-space data at coil c and time t adheres to $$$y_{i,j,k}^{(c)}[t] = [\mathcal{F}(\underline{\mathbf{H}}_c \odot \underline{\mathbf{X}}_t)]_{i,j,k} + v_{i,j,k}[t],~(i,j,k) \in \Omega_t $$$, with $$$\underline{\mathbf{H}}_c $$$ denoting the sensitivity of c-th coil. Assume full k-space data form a 5D data-array $$$\underline{\mathbf{Y}} $$$ indexed by (x,y,z,c,t), the spatiotemporal correlations induces low PARAFAC-rank, namely $$$\underline{\mathbf{Y}} \approx \sum_{r=1}^R \mathbf{a}_r^{(1)} \circ \mathbf{a}_r^{(2)} \circ \mathbf{a}_r^{(3)} \circ \mathbf{a}_r^{(4)} \circ \mathbf{a}_r^{(5)} $$$ for a small rank R, the outerproduct $$$\circ$$$ [2]. Define the factors $$$ \mathbf{A}_i := [\mathbf{a}_1^{(i)}, \ldots, \mathbf{a}_R^{(i)}],~i=1,\ldots,5 $$$ capturing the correlation across spatial (i=1,2,3), temporal (i=5), and coil (i=4) dimensions. The first step to impute missing k-space data pertains to obtaining the factors. To develop efficient algorithms, the data stream is treated as T 4D training-samples spanned by R rank-one tensors. To sequentially learn the factors we optimize the empirical cost
$$\min_{\{\underline{\mathbf{A}}_i\}_{i=1}^4} \frac{1}{T}\sum_{t=1}^T \min_{\boldsymbol{\gamma}}~f_t(\{\underline{\mathbf{A}}_i\}_{i=1}^4;\boldsymbol{\gamma}) $$
where (define $$$\hat{\underline{\mathbf{Y}}}_t^{(c)}:=\sum_{r=1}^R a_{r,t}^{(5)} a_{r,c}^{(4)} \mathbf{a}_r^{(1)} \circ \mathbf{a}_r^{(2)} \circ \mathbf{a}_r^{(3)} $$$)
$$f_t(\{\mathbf{A}_i\}_{i=1}^4;\boldsymbol{\gamma}):=\frac{1}{2} \sum_{(i,j,k) \in \Omega_t} \sum_{c=1}^C w_{i,j,k}^{(c)}[t]\big(y_{i,j,k}^{(c)}[t]-[\hat{\underline{\mathbf{Y}}}_t^{(c)}]_{i,j,k} \big)^2 + \frac{\lambda}{2t} \Big( \rm{tr}(\mathbf{A}_1^{\top} \mathbf{C}_x \mathbf{A}_1) + \rm{tr}(\mathbf{A}_2^{\top} \mathbf{C}_y \mathbf{A}_2) + \rm{tr}(\mathbf{A}_3^{\top} \mathbf{C}_z \mathbf{A}_3) +\|\mathbf{A}_4\|_F^2 \Big) $$
The butterfly-estimated weights compensate for large patient movements [5]. The quadratic regularizer induces low tensor rank [3], and the kernels $$$\mathbf{C}_x,~\mathbf{C}_y,~\mathbf{C}_z $$$, learned from data, incorporate prior information about the spatial structure of k-space. First-order iterative algorithm are derived using stochastic alternating majorization-minimization [3], where iterates are provably convergent, and admit highly parallelizable tasks across bases. Per time instant t, the imputed k-space data across coils are linearly combined $$$\hat{\underline{\mathbf{Y}}}_t=\sum_{c=1}^C \underline{\mathbf{H}}_c^{*} \odot \hat{\underline{\mathbf{Y}}}_t^{(c)} $$$, and subsequently IFFT is applied to reconstruct the 4D image.
Data analysis. K=11.8 fold subsampled k-space data are sequentially fed into the algorithm implemented with Matlab-2016a on a Ubuntu 15.10 machine with 64GB-RAM, and a NVIDIA-GDX-970 GPU. Fixing R=3,000 and λ=0.001, with random initialization, after $$$N_e=5$$$ epochs over data, the latent factors converge. Diagonal matrices $$$\mathbf{C}_x,\mathbf{C}_y,\mathbf{C}_z$$$ are inversely proportional to the average k-space energy along the corresponding directions.
Results
Representative slices depicted in Fig-1 fairly reveal the details. Temporal profile along x- and y-axis also show a smooth motion trajectory. The main complexity per iteration stems from SVD of a sparse matrix $$$\boldsymbol{\Phi} \in \mathbb{C}^{L \times R} $$$ with L=MNPC/K. The overall operation-count for convergence is then safely overestimated as $$$N_e\mathcal{O}(\frac{C}{K}MNPR^2T)$$$, which can be significantly reduced if one leverages the sparsity of $$$\boldsymbol{\Phi} \in \mathbb{C}^{L \times R} $$$. The alternative CS-based scheme in [4] however performs M parallel reconstructions along x, each one running $$$N_i \approx 400$$$ iterations involving a LASSO $$$(N_l)$$$ and TV-regularized $$$(N_{tv})$$$ subproblem. The operation count is around $$$N_i\mathcal{O}(\frac{C}{K} N^3 P^3 T^3 N_{l,t}) $$$, where $$$N_{l,t}:=N_{tv} + N_{l}/T^2 $$$. For the considered dataset, the TSL scheme incurs roughly $$$\mathcal{O}(10^5) $$$ times less operations than CS.Conclusions
An imaging analytic is proposed that efficiently reconstruct high-resolution 4D MR images using GPU computing. Modeling k-space data low-dimensionality with low PARAFAC-rank, correlation across different dimensions are captured via tensor subspace, sequentially learned from the data, to impute the missing k-space entries.Acknowledgements
No acknowledgement found.References
[1] Z. P. Liang et al, ISBI: 988-991, 2007. [2] T. G. Kolda et al, SIAM, 51:455-500. [3] M. Mardani et al, TSP, 2015. [4] J. Y. Cheng et al, MRM, 2015. [5] T. Zhang et al, MRM, 2013. [6] M. Uecker et al, MRM, 2014.Figures
