Synopsis

This work implements a Magnetic Resonance Fingerprinting (MRF) reconstruction that accounts for the presence of multiple compartments in a voxel. We estimate the contributions of the different tissues by incorporating a sparse-recovery method, based on reweighted-l1-norm regularization, within an iterative procedure that fits a multi-compartment model to the measured k-space data. The proposed approach is validated with simulated data, as well as with a controlled phantom experiment. In addition, we present preliminary results on in-vivo measurements of a brain.

Purpose

Theory

In MRF, tissue parameters are estimated by matching the temporal evolution of the MR signal of each voxel to an atom in a dictionary of simulated signals. When the voxel contains several tissues, the MR signal can be approximated by a linear combination of dictionary atoms. The model for the data is $$$y=Dc+z$$$, where $$$D$$$ is the dictionary, $$$z$$$ is additive noise and $$$c$$$ is a sparse vector of coefficients. The nonzero entries correspond to the tissues present in the voxel. Estimating $$$c$$$ is a challenging sparse-recovery problem due to the strong local coherence in the dictionary (nearby dictionary atoms are highly correlated). Consequently, l1-norm regularization, which is successful when the linear operator is incoherent as in compressed sensing², often fails to produce a sparse estimate for $$$c$$$.

We propose to tackle the sparse-recovery problem by solving a sequence of weighted-l1-norm regularized problems of the form:

$$\hat{c}^{(i)}=\arg\min_{c}\;||\,Dc-y\,||_2^2+\lambda\,||\,W^{(i)}c\,||_1,\quad W^{(i)}=\operatorname{diag}\left(\frac{1}{|\hat{c}^{(i-1)}_1|+\epsilon},\frac{1}{|\hat{c}^{(i-1)}_2|+\epsilon},\ldots,\frac{1}{|\hat{c}^{(i-1)}_n|+\epsilon}\right),$$

where $$$i$$$ is the iteration number. The weights penalize the coefficients that do not contribute to the fit in previous iterations, promoting increasingly sparse solutions. Mathematically, the algorithm can be interpreted as a majorization-minimization method for a non-convex sparsity-inducing penalty function³.

Methods

A noisy fingerprint from a single voxel composed of gray matter (GM) and cerebrospinal fluid (CSF) was simulated with SNR=100. An interior-point method⁴ was used to implement traditional l1-norm regularization and the proposed reweighted-l1-norm regularized reconstruction.

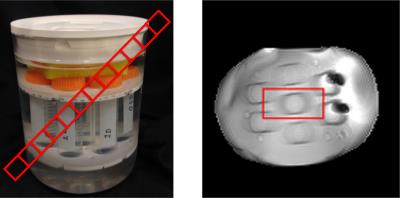
A controlled phantom experiment was carried out (Figure 4). A diagonally-aligned, 20mm-thick slice was imaged with 2mmx2mm in-plane resolution. The alignment produces voxels containing contributions from the tubes and the surrounding fluid, which have different relaxation times. The experiment was performed on a 3T Skyra system (Siemens Healthineers, Erlangen, Germany) with a pseudo-SSFP pattern⁵, which encodes 841 radial spokes with a golden angle⁶ increment. The RF-pattern was repeated 32x with a tiny golden angle increment⁷ and a 10s pause to ensure complete relaxation. The same setup was used to image a healthy volunteer’s brain with IRB-approval. Here, a 4mm transversal slice was imaged with an in-plane resolution of 1mm x 1mm, keeping the rest of parameters the same.

To obtain a multiple-tissue fit over a whole image, we incorporate our sparse-recovery scheme within an iterative procedure based on the alternating-direction method of multipliers^8,9. The algorithm alternates between (1) enforcing consistency between the k-space data and a time series of images and (2) fitting the signal-evolution of each voxel to the simulated dictionary. We solve the linear system that arises in (1) by conjugate gradients. The dictionary matching in (2) is done by the proposed reweighted-l1-norm for each voxel.

Results and Discussion

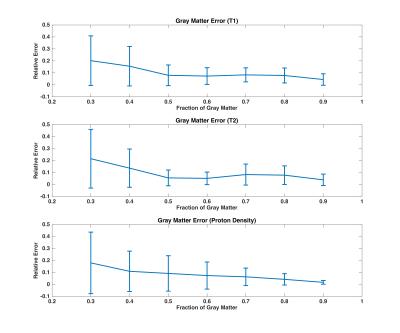
The single-compartment model is not able to fit the simulated data, whereas all multi-compartment reconstructions explain the fingerprint well (Figure 1). We observe that reweighted-l1 regularization allows to successfully fit MRF signals using a small number of dictionary atoms (2 in the present case). In contrast, l1-regularization and Bayesian-based methods produce locally dense solutions as reported in previous work¹⁰. We evaluate the accuracy of the algorithm on simulated noisy data from a voxel containing GM and CSF, which shows increasing noise transfer as the proton density of GM decreases (Figure 2).

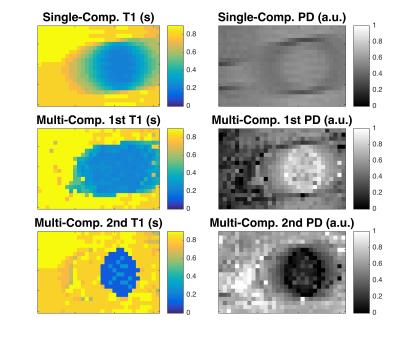
The single-compartment reconstruction of the phantom experiment demonstrates how a mixture of two compartments with different relaxation times corrupt the T₁-maps (Figure 4). In contrast, the two-compartment reconstruction recovers the relaxation times of the central tube and of the surrounding liquid. The slope of the proton density is apparent as the tube infiltrates the slice.

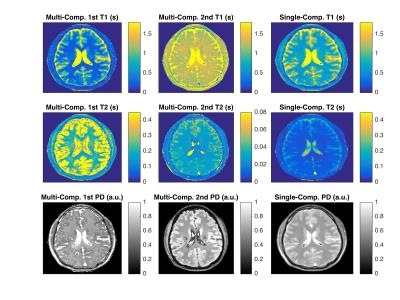
Figure 5 shows preliminary in-vivo results. While the images demonstrate the feasibility of translating our method to in-vivo imaging, further efforts need to be made to understand the underlying physics. The employed sequence has limited sensitivity with respect to T₂, which might explain the questionable T₂-maps⁵. Also, slice-profile imperfections and magnetization transfer are not considered.

Conclusion

Acknowledgements

References

1. Ma D, et al. (2013), Nature 495, 187-92.

2. Lustig M, et al. (2007) Magnetic Resonance in Medicine, 58(6), 1182–1195.

3. Candes E, et al. (2008) Fourier Analysis and Applications, 14(5-6), 877-905.

4. Grant M, Boyd S. (2008) Recent advances in learning and control, 95-110.

5. Asslaender J, et al. (2016) Magn. Reson. Med., p. epub ahead of print.

6. Winkelmann S, et al (2007) IEEE Trans. Med. Imaging, 26(1), pp. 68–76.

7. Wundrak S, et al (2015) IEEE Trans. Med. Imaging, 34(6), pp. 1262–1269.

8. Asslaender J, et al. (2016) Preprint. http://arxiv.org/abs/1608.06974

9. Boyd S, et al. (2011) Foundations and Trends in Machine Learning, 3(1), 1-122

10. McGivney D, et al. (2015), Proc. ISMRM 23, 0435.