3859

Low Rank Alternating Direction Method of Multipliers Reconstruction for MR Fingerprinting

Jakob Assländer^1,2,3, Martijn A Cloos^1,2, Florian Knoll^1,2, Daniel K Sodickson^1,2, Jürgen Hennig³, and Riccardo Lattanzi^1,2

¹Dept. of Radiology - Bernard and Irene Schwartz Center for Biomedical Imaging, New York University School of Medicine, New York, NY, United States, ²Dept. of Radiology - Center for Advanced Imaging Innovation and Research, New York University School of Medicine, New York, NY, United States, ³Dept. of Radiology - Medical Physics, University Medical Center Freiburg, Freiburg, Germany

Synopsis

The proposed reconstruction framework for MR-Fingerprinting (MRF) combines a low rank approximation of the signal's temporal evolution with the alternating direction method of multipliers. This general framework allows for incorporating parallel imaging and compressed sensing. The low rank approximation of the signal's temporal evolution reduces the number of fast Fourier transformations significantly and adresses the non-convexity of the MRF-reconstruction problem. Overall, the convergence is improved and undersampling artifacts are reduced, resulting in a fast, robust and flexible reconstruction framework.

Purpose

MR-Fingerprinting (MRF) reconstructions are commonly^1,2 heuristic two-step procedures: A series of images with different contrasts are reconstructed followed by dictionary matching. Formulating an inverse problem allows for incorporation of parallel imaging^3,4 and compressed sensing⁵. Our proposed framework solves the inverse problem by combining a low rank (LR) approximation of the signal's temporal evolution with the alternating direction method of multipliers (ADMM)^6,7. This improves convergence of this non-convex optimization problem and reduces undersampling artifacts. Further, the low rank approximation reduces the number of fast Fourier transformations (FFT) significantly, resulting in a fast and robust reconstruction framework.

Theory

It has recently been demonstrated that MRF data can be approximated by a low rank representation based on a singular value decomposition of the dictionary². Given a series of images $$$\mathbf{x}\in\mathbb{C}^{NR}$$$ with the number of voxels $$$N$$$ and the rank of the approximation $$$R$$$, the measurement can be described by$$\mathbf{S}=\mathbf{G}\cdot\mathbf{F}_T\cdot\mathbf{U}_R\cdot\mathbf{x}.$$Here, $$$\mathbf{U}_R$$$ is an operator that transforms the series of $$$R$$$ images into a time series, $$$\mathbf{F}_T$$$ performs an FFT for all $$$T$$$ time frames and $$$\mathbf{G}$$$ grids the Cartesian k-space data onto the non-Cartesian trajectory. The vector $$$\mathbf{S}\in\mathbb{C}^K$$$ represents the data at all $$$K$$$ k-space positions acquired in the entire experiment. It can be shown that $$$\mathbf{F}_T\mathbf{U}_R=\mathbf{U}_R\mathbf{F}_R$$$, where $$$\mathbf{F}_R$$$ performs an FFT for each of the $$$R$$$ images. This reduces the computational burden regarding FFTs by a factor $$$R/T$$$. Further, with $$$\mathbf{G}_R=\mathbf{G}\mathbf{U}_R$$$ the gridding operation can be implemented by one sparse matrix that grids the data directly from the low-rank k-space onto the trajectory in the temporal domain. The MRF reconstruction problem can then be formulated as$$\min_{\mathbf{x},\mathbf{{D}}}\parallel\mathbf{G}_R\mathbf{F}_R\mathbf{{D}}\mathbf{{D}}^H\mathbf{x}-\mathbf{S}\parallel_2^2,$$where $$$\mathbf{{D}}\in\mathbb{C}^{NR\times{N}}$$$ is a zero-filled matrix that contains one dictionary atom for each voxel. The product $$$\mathbf{{D}}^H\mathbf{x}$$$ contains scaling factors that reflect the proton density and consequently $$$\mathbf{{D}}\mathbf{{D}}^H\mathbf{x}$$$ is composed of one scaled element of the dictionary for each voxel. The reconstruction problem can be reformulated to the following augmented Lagrangian:$$\min_{\mathbf{x},\mathbf{{D}},\mathbf{y}}\parallel\mathbf{G}_R\mathbf{F}_R\mathbf{x}-\mathbf{S}\parallel_2^2+\mu\parallel\mathbf{x}-\mathbf{{D}}\mathbf{{D}}^H\mathbf{x}+\mathbf{y}\parallel_2^2.$$The first term compares the LR-series of images $$$\mathbf{x}$$$ to the measured data, while the second term couples the series to the dictionary. The coupling parameter $$$\mu\in\mathbb{R}_0^+$$$ influences convergence and the Lagrangian multiplier $$$\mathbf{y}$$$ is denoted in the scaled dual form⁸. This problem is solved by the ADMM algorithm, in which the search variables are optimized alternately. The subproblem of optimizing $$$\mathbf{x}$$$ is a linear problem that is solved by a conjugate gradient algorithm. The subproblem of solving for $$$\mathbf{D}$$$ represents the dictionary matching, which is done by exhaustive search, and $$$\mathbf{y}$$$ is updated as proposed in the ADMM framework⁸.

Methods

Simulations were performed with a numerical phantom⁹ and a pseudo steady-state free precession (pSSFP) sequence⁷ with a radial k-space readout. The proposed LR-ADMM algorithm is compared to a filtered back-projection² followed by the dictionary matching. The root mean square error (RMSE) of the proton density (PD), $$$T_1$$$ and $$$T_2$$$ in white matter were calculated for multiple $$$R$$$-values. The signal to noise ratio (SNR) was calculated based on 100 pseudo-replicas. A transversal slice of a volunteer's brain was scanned with a 3T Prisma (Siemens Healthineers, Erlangen, Germany) with IRB-approval. The data have a resolution of $$$1\text{mm}\times1\text{mm}\times3\text{mm}$$$ and a matrix size of $$$256\times256$$$. Overall, 754 radial spokes were acquired within 3.3s. The employed pseudo-SSFP sequence and parameters match those used in⁷.

Results and Discussion

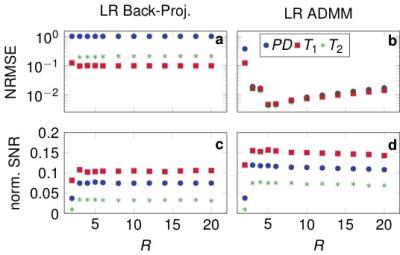
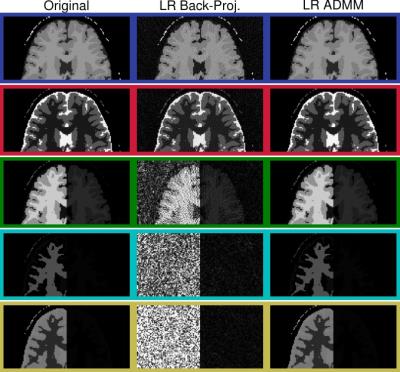
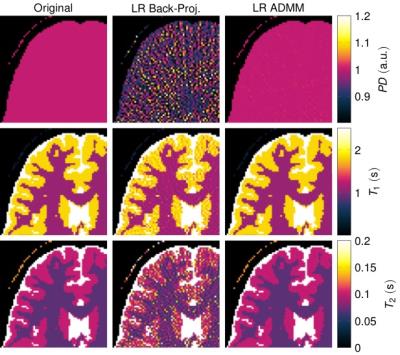
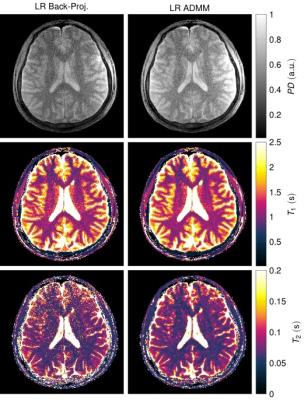
Figure$$$~$$$1 demonstrates the rapid decrease of the singular values. The quantitative maps reconstructed with the proposed LR-ADMM algorithm show a considerably lower RMSE and higher SNR compared to the back-projection (Figure$$$~$$$2). In the case of the LR-ADMM reconstruction, the RMSE has a minimum at $$$R=5$$$. At a lower rank, the data is not well-represented, leading to an increased RMSE. On the other hand, the reconstruction is increasingly ill-conditioned for large $$$R$$$ values, leading to bigger undersampling artifacts and ultimately a higher RMSE. This is particularly the case for an ADMM reconstruction without a low rank approximation^6,7, which is equivalent to the proposed reconstruction with $$$R=T=850$$$. The LR-images and the quantitative maps reconstructed with the optimal $$$R=5$$$ in Figure$$$~$$$3,4 show reduced noise-like undersampling artifacts when employing the LR-ADMM algorithm. Please note that these simulations are based on noise-free data.The reconstructions of the in-vivo data (Figure$$$~$$$5) confirm the reduced artifact level when employing the LR-ADMM algorithm. This particular data-set took 43s to reconstruct on a desktop computer (3.3GHz Intel i5-6600 processor).

Conclusion

To conclude, the proposed reconstruction reduces the computational burden and improves image quality. The general formulation as an inverse problem allows for further incorporation of priors. Future work will explore compressed sensing approaches that couple the series of images, for example by penalizing the nuclear norm of the spatial gradient^10,11.

Acknowledgements

This work was supported in part by the research grants NIH R21 EB020096 and was performed under the rubric of the Center for Advanced Imaging Innovation and Research(CAI2R, www.cai2r.net), a NIBIB Biomedical Technology Resource Center(NIH P41 EB017183).

References

1. Dan Ma, Vikas Gulani, Nicole Seiberlich, Kecheng Liu, Jeffrey L. Sunshine, Jeffrey L. Duerk, and Mark A. Griswold. Magnetic resonance fingerprinting. Nature,495(7440):187–192, 2013.

2. Debra; McGivney, Dan; Ma, Haris; Saybasili, Yun; Jiang, and Mark Griswold. Singular Value Decomposition for Magnetic Resonance Fingerprinting in the Time Domain. IEEE transactions on medical imaging, 33(12):2311–2322, 2014.

3. Daniel K. Sodickson and Warren J. Manning. Simultaneous acquisition of spatial harmonics (SMASH): Fast imaging with radio frequency coil arrays. Magnetic Resonance in Medicine, 38(4):591–603, 1997.

4. Klaas P. Pruessmann, Markus Weiger, Peter Börnert, and Peter Boesiger. Advances in sensitivity encoding with arbitrary k-space trajectories. Magnetic Resonance in Medicine, 46(4):638–651, 2001.

5. Michael Lustig, David Donoho, and John M. Pauly. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine,58(6):1182–1195, 2007.

6. Bo Zhao, Kawin Setsompop, Huihui Ye, Stephen Cauley, and Lawrence Wald. Maximum Likelihood Reconstruction for Magnetic Resonance Fingerprinting. IEEE Transactions on Medical Imaging, page epub ahead of print, 2016.

7. Jakob Assländer, Steffen J Glaser, and Jürgen Hennig. Pseudo Steady-State Free Precession for MR-Fingerprinting. Magnetic Resonance in Medicine, page epub ahead of print, 2016.

8. S Boyd, N Parikh, B Peleato E Chu, and J Eckstein. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Foundations and Trends in Machine Learning, 3(1):1–122, 2011.

9. D L Collins, A P Zijdenbos, V Kollokian, J G Sled, N J Kabani, C J Holmes, and A C Evans. Design and construction of a realistic digital brain phantom. IEEE transactions on medical imaging, 17(3):463–468, 1998.

10. Florian Knoll, Martin Holler, Thomas Koesters, Ricardo Otazo, Kristian Bredies, and Daniel K Sodickson. Joint MR-PET reconstruction using a multi-channel image regularizer. IEEE Transactions on Medical Imaging, page epub ahead of print, 2016.

11. Florian Knoll, Martin Holler, Thomas Koesters, Martijn Cloos, Ricardo Otazo, Kristian Bredies, and Daniel K Sodickson. Simultaneous multi-modality/multi-contrast image reconstruction with nuclear-norm TGV. In Proc. Intl. Soc. Mag. Reson. Med. 24,page 873, 2016.6

Figures

Figure 1: The flip angle pattern of the employed pseudo-SSFP sequence⁷ is depicted in (a), while (b) shows the first five left singular vectors (columns of $$$\mathbf{U}_R$$$), which result from the singular value decomposition of the dictionary and were used for the low rank approximation unless stated otherwise. Their color-coding corresponds to (c), where the first ten singular values of the dictionary are shown.

Figure 2: The normalized root mean square error (NRMSE) in white matter is shown (a,b) as a function of the rank used to approximate the signal evolution. The NRMSE for a rank 2 approximation is not displayed for $$$T_2$$$ since the values are too large for the displayed area. The $$$PD$$$-, $$$T_1$$$- and $$$T_2$$$-to noise ratio in white matter are shown in (c,d) normalized by the input SNR.

Figure 3: The series of images $$$\mathbf{x}$$$ reconstructed from noise free synthetic data are shown. The rows correspond to the singular values in decreasing order and their color coding corresponds to Figure 1 (b,c). The columns show the different low rank (LR) reconstruction techniques discussed in this abstract. Only the top half of the images are shown for better depiction. The right hand side of all images are scaled equally, while the left hand side is scaled equally only within the same row.

Figure 4: The displayed excerpts of quantitative maps compare the discussed reconstruction methods. The simulations are based on a numerical phantom and the maps correspond to the singular value images shown in Figure 3. For the simulation, a unit proton density was used since it's influence is linear and a constant value allows for a better depiction of errors. The maps were reconstructed from noise free data using $$$R=5$$$ singular values.

Figure 5: The depicted parameter maps with a matrix size of $$$256\times256$$$ were reconstructed from 754 radial spokes, which were acquired in-vivo within 3.3s. Coil sensitivity profiles of a 44 channel head coil (compressed to 12 virtual coil elements) were incorporated for a SENSE⁴-like reconstruction.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

3859