Synopsis

Non-Cartesian multi-shot sequences (e.g. spiral) offer several benefits over Cartesian counterparts in the context of high spatial resolution diffusion weighted imaging (DWI), including reduced B₀ & T2* artifacts, as well as improved SNR resulting from lower TE. However, their main drawback of the above scheme is the sensitivity of the multi-shot imaging to motion artifacts. To achieve motion compensation, the multi-shot reconstruction methods rely on a phase-calibration procedure, during which an estimate of motion induced phase map is computed. Not only is the phase-calibration step time consuming, it also involves heavy optimization of parameters. The main focus of this work is to develop a phase calibration-free motion-compensated reconstruction for multi-shot non-Cartesian diffusion imaging.

Introduction

Methods

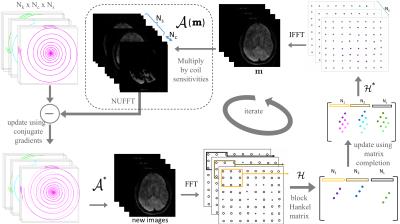
The bulk motion during diffusion gradients results in the DWI of each shot being modulated by a spatially varying phase³. We recently developed a structured low-rank matrix completion formulation to compensate for such phase terms in multi-shot Cartesian DWI data⁴. The central idea is that image domain phase distortions can be modeled as the convolution between the k-space data and a small filter. In particular, if two images differ only by a smoothly varying phase, we can find an annihilation filter that can capture the phase errors. We compactly captured these annihilation relations using a low-rank block-Hankel structured matrix, whose entries are the k-space samples of the shots. We filled in the missing entries of the Hankel matrix using a low-rank matrix completion algorithm. In this work, we generalize this method to non-Cartesian trajectories; the main challenge is that the measurements in the non-Cartesian setting do not directly correspond to the entries of the Hankel matrix.

We formulate the reconstruction as the following nuclear norm penalized optimization problem:\begin{equation}\tilde {\bf m}= \text{argmin}_{{\bf {m}}} {||\bf{{\cal{A}}({m})-\hat y}}||^2_{\ell_2} + \lambda||{\bf{\cal{H}}_1(\hat{m})}||_* , \end{equation} where, $$$\bf{\hat{y}}$$$ is the matrix of measured multi-channel multi-shot k-space data. Here, $$$\bf m$$$ correspond to the multi-shot images, and $$$\hat {\bf m}$$$ denotes its Fourier coefficients, both on a Cartesian lattice. The operator $$$\bf{{\cal{A}}}$$$ corresponds to the sensitivity weighted non-Cartesian Fourier transform of the shots, which are efficiently evaluated using NUFFT operations. The structure of the block-Hankel matrix is the same as in our previous work⁴ and is illustrated in Figure 1. We solve the above nuclear norm minimization problem using an ADMM algorithm.

The diffusion data, acquired using a variable density spiral acquisition employing an 8-channel head coil was used to validate the algorithm. The diffusion imaging used a b-value=1200s/mm², 30 diffusion directions and one non-diffusion weighted acquisition, with 22 spiral interleaves and a variable density factor of 4. Other parameters: FOV= 192mmx192mm; matrix size=192x192, slice thickness=1.5mm, TE=52ms.

Results

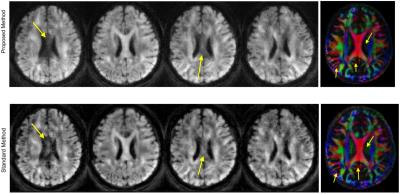
Preliminary results from our proposed method are shown in Figure 2. The proposed method, which does not require phase calibration is shown to achieve good motion-compensated recovery for multi-shot non-Cartesian data. The reconstruction of four DWIs and the direction-encoded color (DEC) map of fractional anisotropy reconstructed using the proposed method is compared with the standard method⁵, that performs phase calibration to recover the motion-compensated DWI. The phase-calibrated method works well for most diffusion directions, while it fails for certain diffusion directions. The first and third diffusion directions, where the phase estimation is erroneous leading to incomplete motion compensation, are shown in Figure 2. The calibration-free method is shown to achieve good motion compensation for all the DWIs. The DEC maps obtained from the 30 diffusion directions of both reconstructions show differences as indicated by the arrows.

Note that the spiral acquisition used in this work, with the oversampled k-space center, is ideally suited for the standard calibration-based methods, since the phase estimation is expected to work well in such cases. In general, trajectories with less over-sampled k-space center (e.g., uniform density spirals) are better suited for high spatial resolution applications due to their shorter readouts and insensitivity thereof to $$$B_0$$$ artifacts. Based on our experience with multi-shot EPI recovery using calibrated and calibration-free methods, we expect higher performance improvement with the proposed method in such uniformly sampled setting.

Conclusion

Acknowledgements

References

1. Liu, C., Bammer, R., Kim, D.-h. and Moseley, M. E. (2004), Self-navigated interleaved spiral (SNAILS): Application to high-resolution diffusion tensor imaging. Magn Reson Med, 52: 1388-1396. doi: 10.1002/mrm.20288.

2. N.-K. Chen, A. Guidon, H.-C. Chang, and A. W. Song. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). NeuroImage, 72:41-7, 2013. ISSN 1095-9572.

3. A. W. Anderson and J. C. Gore. Analysis and correction of motion artifacts in diffusion weighted imaging. MagnReson Med., 32(3):379-87, 1994.

4. Mani, M., Jacob, M., Kelley, D. and Magnotta, V. (2016), Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn Reson Med. doi: 10.1002/mrm.26382.

5. Liu C, Moseley ME, Bammer R. Simultaneous phase correction and SENSE reconstruction for navigated multi-shot DWI with non-cartesian k-space sampling. Magn Reson Med 2005;54:1412-1422.