3857
High frame rate vocal tract MRI using compressed sensing on randomly sampled Cartesian spoiled fast gradient echo1IADI, Université de Lorraine, Nancy, France, 2U947, INSERM, Nancy, France, 3LORIA, INRIA/CNRS/Université de Lorraine, Nancy, France, 4CIC-IT 1433, CHRU Nancy, Nancy, France
Synopsis
MRI becomes an important tool in the study of speech, in particular in the understanding of articulatory gestures. Distributed Compressed Sensing and Projection Onto Convex Sets are used to reconstruct dynamic sequences of vocal tract images at 33 frames per second with a spatial resolution enabling the extraction of vocal tract contours. 15 seconds long, spoiled gradient echo sequence acquisitions with pseudo random Cartesian sampling were recorded while subjects were repeating sentences. 76 sentences were recorded, representing the majority of the French phonemes. High frame rate dynamic vocal tract MRI will enable the study of coarticulation in French.
PURPOSE:
Studying speech production requires acquisition of articulatory gestures together with the speech acoustic signal. The articulatory gestures change the vocal tract geometry and thus acoustic properties of speech. Coordination of articulatory gestures have a time scale of hundred milliseconds. Therefore, a frame rate of 30 Hz is needed. It gives approximately two images for each speech sound. MRI plays an increasing role in the study of speech (1–3). Historically, speech MRI has used spiral sampling to enhance the acquisition rate. Here, the proposed framework uses a Cartesian sampling enabling the use of compressed sensing (4) and homodyne reconstruction (5). This framework simultaneously integrates several MRI acceleration techniques applied in an articulatory data acquisition.METHODS:
MRI experiments were performed on a 3T Signa HDxt MR system (GE Healthcare, Milwaukee, WI). Dynamic vocal tract MRI data were obtained form 3 healthy volunteers with written informed consent and approval of local ethics committee. The data were collected with a 16 channel neurovascular coil array. The protocol consisted in a mid-sagittal vocal tract slice acquired with a custom modified Spoiled Fast Gradient Echo (FSPGR, TR 3.02ms , TE 1.004ms, partial Fourier 120 $$$k_x$$$ samples, line BW 125 kHz, flip angle 30°, matrix 192x192, 512 temporal frames). For each temporal frame the sequence modification consisted in acquiring only a randomized subset of lines per frame ($$$n_{lpf}=10$$$) among the phase lines ($$$n_y=192$$$) of the k-space, resulting in an acquisition time of $$$3.02ms\times n_{lpf}$$$ per frame and a total acquisition time of $$$512\times 3.02\times n_{lpf}=15.5s$$$. During the acquisition protocol all subjects had to pronounce a set of 76 French sentences chosen to span the largest coarticulation context. Each sentences was pronounced several times during the 15.5s acquisition and the voice was recorded.
A pseudo-random Cartesian sampling scheme is chosen were central k-space lines are privileged. With $$$n_{lpf}=10$$$, the number of fully sampled centre lines is set $$$n_{cl}=5$$$. For each temporal frame the $$$n_{cl}$$$ central lines are fully sampled and the remaining lines are randomly chosen following the probability function:
$$p\left(k_y,t\right)=\left|\frac{1}{\left(1-\left(k_y-\frac{n_y}{2}\right)\right)^{r(t)}}\right|$$
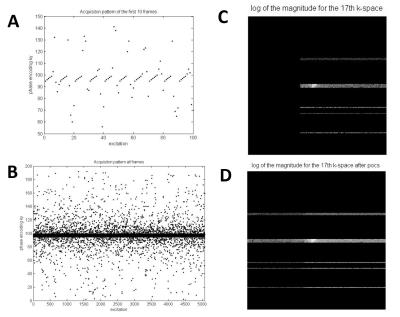
This distribution leads to a variable sampling density that decreases away from the centre k-space lines as displayed in Figure 1.
Since the acquisition uses partial Fourier in $$$k_x$$$ direction a fist iterative homodyne k-space filling for each coil using POCS (Projection Onto Convex Sets) (5) is used to recover the full k-space lines. To build the low resolution images used as phase correction prior in the POCS algorithm the temporal mean value of the acquired kt-space for the whole acquisition is used.
As presented in more details in (6), the temporal Fourier of the image intensity is chosen as a sparse-transform to apply the compressed sensing. Using parallel acquisition on multichannel coils, compressed sensing can exploit the strong correlation of the different channels by introducing a joint sparsity constraint by simultaneously minimizing the $$$l_1\rm{-norm}$$$ of the sparse representation of the signal in each coil and also the number of non-zero coefficients location for all coils. Therefore a Distributed Compressed Sensing (DCS) (7) with these assumption is performed.
By using the complete k-space lines form the POCS iterative reconstruction as an observation matrix $$$\bf{B}$$$, the DCS reconstruction is performed solving the equation:
$$\bf{P}\it{=}\underset{{\bf\hat{P}}}{\operatorname{argmin}}\|{\bf{F}_{\it{t}}}{\bf{\hat{P}}}\|_{1,2}\qquad{s.t.}\qquad\|{\bf{\Phi}}{\bf{F}_{\it{sp}}}{\bf\hat{P}}-\bf{B}\|_{\it2,2}\leq\epsilon$$
Where $$$\bf{P}$$$ is the matrix whose columns contain the images vectors of the $$$l$$$ colis. $$$\bf{F}_{\it{t}}$$$ is the time Fourier and $$$\bf{F}_{\it{sp}}$$$ is the spatial Fourier operators. $$$\bf{\Phi}$$$ is the incoherent acquitition matrix issue from the pseudo-random Cartesian sampling. The $$$l_{1,2}\rm{-norm}$$$ is defined as the $$$l_1\rm{-norm}$$$ of the $$$l_2\rm{-norm}$$$ of each row of $$$\bf{P}$$$. To solve this equation SPGL1 solver (8,9) was used.
Finally coils combination is performed for each frame to produce the final vocal tract movie.
RESULTS:
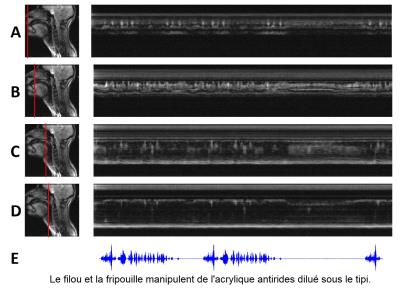
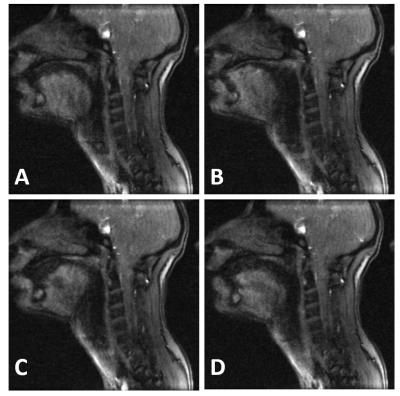
For the 3 subjects, 93 vocal tract acquisition have been collected. In Figure 2 is displayed one reconstructed dynamic movie with time motion images for selected positions in the vocal tract. In Figure 3, the images quality of four randomly selected images form the same movie give a sample of the image quality enabling vocal tract segmentation.DISCUSSION:
For one acquisition reconstruction took 29h08min, on 8 core Xeon at 3GHz for 527 iterations. Matlab reconstruction can be thither optimised. Processing of 24 minutes long total movie is still ongoing.CONCLUSION:
The presented protocol for acquiring 2D sagittal movies of the vocal tract will enable articulator contours to be extracted with a temporal resolution of 30.2ms. These acquisitions on 3 subjects with a set of 76 sentences presenting all possible phonetic variability of coarticulation in French will enable the creation of an articulatory model of speech production for French.Acknowledgements
The authors thank French ANR, FEDER and Région Lorraine for their financial support.References
1. Scott AD, Wylezinska M, Birch MJ, Miquel ME. Speech MRI: morphology and function. Phys. Medica PM Int. J. Devoted Appl. Phys. Med. Biol. Off. J. Ital. Assoc. Biomed. Phys. AIFB 2014;30:604–618. doi: 10.1016/j.ejmp.2014.05.001.
2. Fu M, Zhao B, Carignan C, Shosted RK, Perry JL, Kuehn DP, Liang Z-P, Sutton BP. High-resolution dynamic speech imaging with joint low-rank and sparsity constraints. Magn. Reson. Med. 2015;73:1820–1832. doi: 10.1002/mrm.25302.
3. Lingala SG, Zhu Y, Kim Y-C, Toutios A, Narayanan S, Nayak KS. A fast and flexible MRI system for the study of dynamic vocal tract shaping. Magn. Reson. Med. 2016. doi: 10.1002/mrm.26090.
4. Donoho DL. Compressed sensing. IEEE Trans. Inf. Theory 2006;52:1289–1306. doi: 10.1109/TIT.2006.871582.
5. Youla D. Generalized Image Restoration by the Method of Alternating Orthogonal Projections. IEEE Trans. Circuits Syst. 1978;25:694–702. doi: 10.1109/TCS.1978.1084541.
6. Elie B, Laprie Y, Vuissoz P-A, Odille F. High spatiotemporal cineMRI films using compressed sensing for acquiring articulatory data. In: EUSIPCO2016. Budapest, Hungary; 2016.
7. Liang D, Liu B, Wang J, Ying L. Accelerating SENSE using compressed sensing. Magn. Reson. Med. 2009;62:1574–1584. doi: 10.1002/mrm.22161.
8. van den Berg E, Friedlander M. SPGL1: A solver for large-scale sparse reconstruction http://www.cs.ubc.ca/~mpf/spgl1/index.html.
9. van den Berg E, Friedlander M. Probing the Pareto Frontier for Basis Pursuit Solutions. SIAM J. Sci. Comput. 2008;31:890–912. doi: 10.1137/080714488.
Figures