3855
Improved Accelerated Model-based Parameter Quantification with Total-Generalized-Variation Regularization.1Institute of Medical Engineering, Graz University of Technology, Graz, Austria, 2Institute of Mathematics and Scientific Computing, University of Graz, Graz, Austria, 3Insitute for Computer Graphics and Vision, Graz University of Technology, Graz, Austria
Synopsis
Incorporating TGV-regularization to accelerated model-based parameter-quantification can lead to improved image quality, however, adds non-differentiability to the problem which poses a problem for commonly used first order optimization methods like non-linear Conjugate-Gradient. The proposed method overcomes this limitation by handling the problem within a Gauss-Newton-framework and applying a Primal-Dual-algorithm to solve the inner TGV-regularized problem. Numerical simulations exhibit high agreement to references for four different parameter mapping problems up to 18-fold acceleration. In-vivo results for T1-VFA and T2-MESE models strengthen these findings. The proposed method offers huge acceleration potential for model-based parameter-quantification with similar quantification quality as fully sampled data.
Purpose
The use of Total-Generalized-Variation (TGV) regularization for accelerated MR image reconstruction was shown to substantially improve image quality1,2,3. In this work we adapt this successful regularization strategy to model-based parameter quantification (MBPQ) from highly undersampled data. In distinction to conventional image reconstruction, MBPQ involves solving non-linear and often non-convex optimization problems. TGV regularization adds non-differentiability to these restrictions and prevents common optimization algorithms like non-linear Conjugate-Gradient4,5 (CG) from being used. Thus, we propose a solution strategy based on the Gauss-Newton (GN) method, that allows for incorporation of non-smooth regularization and illustrate its general applicability for distinct MR parameter quantification tasks.Methods
MBPQ problems can be described by a data fidelity term, reflecting the mismatch between the physical model and measured data, and a regularization term $$$R(x)$$$ that accounts for numerical stabilization and enforces a-priori information on the unknown parameters $$$x$$$. $$\underset{x}{\min}\frac{\lambda}{2}\|A(x)-d\|^2_2+R(x)$$ The model $$$A(x)$$$ consists of receiver coil sensitivites, Fourier Transform, k-space sampling pattern and a model-specific connection between sequence parameter variations and MR signal and is typically non-linear. By linearization of $$$A$$$, termed $$$DA$$$ (Gauss-Newton method) the non-convex problem above rewrites as $$\underset{x}{\min}\frac{\lambda}{2}\|DAx-d_k\|^2_2+R(x)+\frac{1}{2\gamma}\|x-x_k\|_2^2$$ where $$$d_k$$$ contains the data and constant terms of the linearization. This problem is the inner problem of the Gauss-Newton method and has to be solved in every linearization step. In case of TGV-regularization a Primal-Dual (PD) algorithm6 with line-search7 is used for optimization. $$$\|x-x_k\|_2^2$$$ serves as step size restriction on the inner optimization problem ($$$x_k$$$ linearization-point).
The proposed method was validated on different MBPQ problems and compared to GN with Tikhonov regularization, i.e. $$$R(x)=\|x\|_2^2$$$ (GN-Tikh). T1 was quantified using a model for an Inversion-Recovery-Look-Locker(IR-LL) sequence8,9 and with the Variable-Flip-Angle model (VFA)10,11,12. For T2 quantification the standard mono-exponential model of T2 decay (MESE) was used as well as a VFA approach11,12. First, numerical Shepp-Logan phantom data was generated and artificially subsampled to validate the algorithm. In a second step this subsampling was applied to VFA-T1 and MESE-T2 in-vivo datasets.
The numerical T1 phantom consisted of areas with 3000/1200/800ms, the T2 of 1200/120/80ms. Artificial coil sensitivities were generated with Biot-Sarvats law. Data for VFA- and IR-LL models was undersampled by $$$AF\in\{1,6,12,18\}$$$ using a variable-density pseudo-random pattern13. For MESE data, a pseudo-radial pattern was used since data was acquired slice by slice. All phantoms were 128x128x1 in size and a reasonable amount of Gaussian noise was added to every coil data. A constant value for T1 and T2 was used as an initial guess except for the VFA approach where a low-resolution DESPOT111,12 fit was used. Coil sensitivities were estimated with the method of Uecker et al.14. B1 correction for VFA was done using the Bloch-Siegert approach15. VFA-T2 was initialized with the results of the VFA-T1 fit and a constant value for T2.
In-vivo data for the VFA model was acquired in 3D. For reconstruction, a FFT in z-direction was applied and undersampling was performed retrospectively in 2D on the central slice. For evaluation, segmentation of gray and white matter was carried out using atlas-based registration with the SPM12-Toolbox. Fully sampled references were generated with DESPOT-T1-method and pixel-wise MESE-exponential fit.
Results
T1 quantification of simulated data with the proposed method is shown in Figure 1a on the left, the GN-Tikh references are shown on the right. Parameter maps are displayed in ms. Results for T2 quantification are given in Figure 1b. Quantitative evaluation of three different ROIs, corresponding to the three phantom regions, are show as boxplot in Figure 2. In-vivo results for VFA-T1 and MESE-T2 quantification are shown in Figure 3 a) and b), respectively. Boxplots for segmented gray and white matter and increasing acceleration are given in Figure 4.
Discussion
Parameter maps for numerical phantoms are in accurate agreement with the numerical references even for high acceleration factors. Compared to GN-Tikh the proposed method shows lower noise levels for high acceleration and more accurate quantification. VFA models deviate more from the numerical references compared to IR-LL and MESE, which could be due to the more complex signal behavior and reduced information content (10/13 vs. 30 measurements). In-vivo results correspond well to the references up to acceleration of 18. However, by optimizing the regularization parameter in dependence on acceleration and spatial information even better results can be expected.Conclusion
The proposed method offers significant acceleration potential and overcomes the limitation of non-linear CG regarding regularization. Furthermore, we have shown that the method is not limited to a specific model. Substantial improvement in image quality and quantification compared to GN-Tikh could be observed for the VFA-T1 model, in particular.Acknowledgements
Funded by the Austrian Science Fund (FWF) SFB F3209-18; "HTI:Tech for Med" (ABT08-22-T-7/2013-13); NVIDIA Corporation Hardware grant supportReferences
1. Bredies K, Kunisch K, Pock T. Total Generalized Variation. SIAM J Imaging Sci. 2010;3(3):492-526.
2. Knoll F, Bredies K, Pock T, Stollberger R. Second order total generalized variation (TGV) for MRI. Magn Reson Med 2011; 65(2):480-91.
3. Knoll F, Clason C, Bredies K, Uecker M, Stollberger R. Parallel Imaging with Nonlinear Reconstruction using Variational Penalties. Magn Reson Med 2012; 67(1):34-41.
4. Block KT, Uecker M, Frahm J. Model-Based Iterative Reconstruction for Radial Fast Spin-Echo MRI. IEEE Transactions on Medical Imaging, Vol. 28, No. 11, November 2009
5. Sumpf TJ, Uecker M, Boretius S, Frahm J. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI. J Magn Reson Imag 2011; 34(2):420–428
6. Chambolle A, and Pock T. A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of Mathematical Imaging and Vision 2011; 40(1):120--145.
7. Maltisky Y, Pock T. A first-order primal-dual algorithm with linesearch. arXiv:1608.08883v1 [math.OC]
8. Henderson E, McKinnon G, Lee TY, Rutt BK. A Fast 3D Look-Locker Method for volumetric T1 Mapping. Magn Reson Imaging. 1999 Oct;17(8):1163-71.
9. Tran-Gia J, Wech T, Bley T, Köstler H. Model-Based Acceleration of Look-Locker T1 Mapping. PLoS ONE 10(4): e0122611
10. Homer J, Beevers MS. Driver-equilibrium single-pulse observation of T1 relaxation. A re-evaluation of a rapid “new” method for determining NMR spin-lattice relaxation times. J Magn Reson 1985; 63: 287--297.
11. Deoni SC, Rutt BK, Peters TM. "Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state." Magn Reson Med 2003; 49: 515-526.
12. Deoni SC, Peters TM, Rutt BK. High-resolution T1 and T2 mapping of the brain in a clinically acceptable time with DESPOT1 and DESPOT2. Magn Reson Med 2005; 53: 237–241.
13. Knoll F, Clason C, Diwoky C, Stollberger R. Adapted random sampling patterns for accelerated MRI. MAGMA 2011 24: 43-50
14. Uecker M, Hohage T, Block KT, Frahm J. Image reconstruction by regularized nonlinear inversion—joint estimation of coil sensitivities and image content. Magn. Reson. Med. 2008; 60:674-82
15. Sacolick LI, Wiesinger F, Hancu I, Vogel MW. B1 mapping by Bloch-Siegert shift. Magn. Reson. Med. 2010; 63:1315-22
Figures
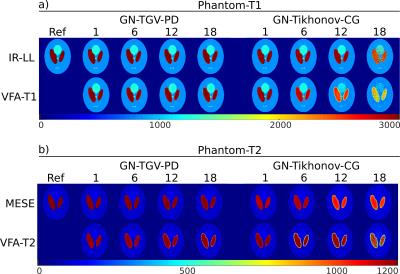
Figure 1: Comparison between the proposed GN-TGV method, on the left, and standard Tikhonov regularization within the GN framework, on the right, for different T1 and T2 quantification models. a) shows the T1-models for increasing acceleration. The numerical reference T1 is in the top left corner. Part b) of the figure shows the reconstruction for different T2 models. All values are given in milliseconds.
IR-LL parameters: TE=2.5ms, dead time Td=4.3ms, sample spacing τ=200ms, wait time Tr=1000ms, α=10°, 30 simulated images.
VFA-T1 (FLASH) parameters: TR/TE=3.4/1.1ms, FA=1/3/5/7/9/11/13/15/17/19°.
MESE parameters: TR/TE=5000/20ms, ΔTE=20ms, 30 images simulated.
VFA-T2 (bSSFP) parameters: TR/TE=5/2ms, FA=5/8/11/14/17/20/23/26/29/32/35/70°.
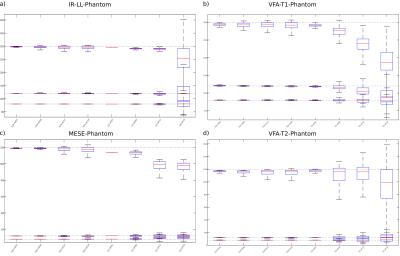
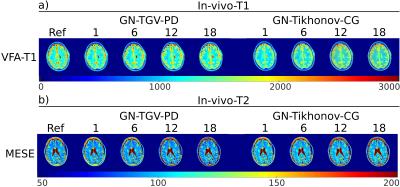
Figure 3: In-vivo example reconstructions for a) VFA-T1 and b) MESE-measurements. Left part of the Figure shows the reconstruction with the proposed method for increasing accelaration, right part the reference method with GN-Tikh, the fully sampled references are on the very left. All values are given in milliseconds.
VFA-T1 (FLASH) parameters: TR/TE=5.41/2.46ms, FA=1/3/5/7/9/11/13/15/17/19°, 256x256x32 matrix with 1x1x3mm3.
MESE parameters: TR/TE=3110/11, ΔTE=11ms, 256x256x32 matrix with 1x1x5mm3. First echo neglected for fitting.
