Synopsis

The CAIPIRINHA (Controlled Aliasing in Parallel Imaging Results in Higher Acceleration), proposed for simultaneous multislice imaging, combines the multiband excitation and phase cycling techniques to reduce scan time and improve the subsequent imaging reconstruction.The total variation (TV) regularization uses an edge-preserving prior which imposes a relationship between neighboring pixels for image reconstruction. In this work, the TV regularization method is applied to further improve the CAIPIRINHA. In vivo data results demonstrate that the TV regularization is very powerful in suppressing noise, maintaining fine imaging details and reducing aliasing artifacts.

Introduction

Methods

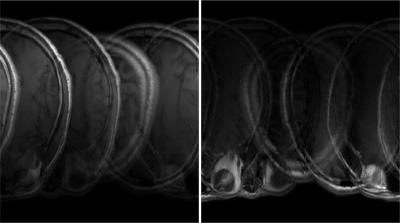
For the purpose of identifying the effects of the TV regularization to the CAIPIRNHA, in vivo data were acquired from human brain on a Philips 3T MRI scanner using a normal spin-echo sequence with imaging parameters as follows: TR/TE = 490 ms/11.6 ms, matrix size = 256 196, field of view = 230 198 mm2, number of slices = 18, slice thickness = 4 mm, slice gap = 1mm. The imaging data was acquired with an eight-channel head coil. A simultaneously excited data was derived from the summation of four slices (these slices were chosen from the acquired 18 slices: the 1st, 3rd, 8th and 10th slices) with different phase cycles: 0, π/2, π, 3π/2. Fig. 1 shows the two of the channel images. Coil sensitivity profiles of the excited four slices were obtained by the self-calibration method using 48 phase-encoding lines at the center of their k-space⁵. Then, a fixed-point iteration algorithm was used to solve the non-linear minimization problem of equation:

$${{f}_{TV}}=\underset{f}{\mathop{\arg }}\,\ \min \left\{ \ \left\| Ef-d \right\|_{2}^{2}+\lambda \sum{\sqrt{{{\left| {{\nabla }_{x}}f \right|}^{2}}+{{\left| {{\nabla }_{y}}f \right|}^{2}}}} \right\} [1]$$

where f is the unfolded images , d is the acquired k-space data from all the channels, and denote the gradient along x and y direction in the 2D image, respectively, and | | denotes the complex modulus. The λ is the TV regularization parameter. E is the spatial encoding matrix combined with gradient and coil sensitivity encodings and the matrix element is as follows:$${{E}_{r,c}}={{C}_{ns,j}}(x,y-\Delta y)exp(in\Delta {{k}_{y}}\Delta y)\exp (-im\Delta {{k}_{x}}x)\exp (-in\Delta {{k}_{y}}y) [2]$$

In addition, CG iteration reconstruction was also implemented for comparison. For quantitative comparison, the normalized mean squared error (NMSE) is defined as the normalized square of the difference between the reconstructed image (Irec) and the reference standard image (ISOS: it was obtained by sum-of-square (SOS) method for each single acquired slice). And the NMSE is expressed as follows:$$NMSE=(\sum\limits_{(x,y)}{{{\left| \left| {{I}_{rec}}(x,y) \right|-\left| {{I}_{sos}}(x,y) \right| \right|}^{2}})}/(\sum\limits_{(x,y)}{{{\left| {{I}_{sos}}(x,y) \right|}^{2}}})) [3]$$

Results

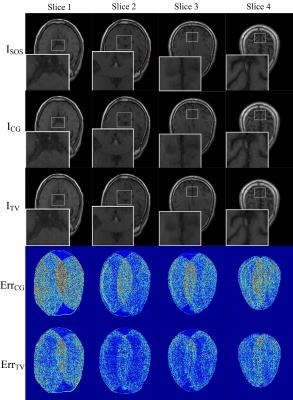
The first three rows in Fig. 2 shows the obtained four slices produced by SOS, CG and TV reconstruction methods. The same regions in all the images are amplified for better comparison. Noise can be seen in the images by CG reconstruction and the images using TV based reconstruction almost have the same image quality as the standard SOS images.

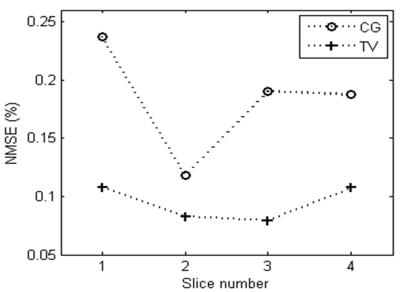
The error maps calculated by the two equations: $$$Er{{r}_{CG}}=\left| {{I}_{CG}}-{{I}_{SOS}} \right|$$$ and $$$Er{{r}_{TV}}=\left| {{I}_{TV}}-{{I}_{SOS}} \right|$$$ are shown in the fourth and fifth rows in Fig. 2. They were normalized and displayed with a same color scale. Both the intensities of noise and artifacts are smaller and lower in the TV images than the CG images. The NMSE values are shown in Fig. 3 which presented the total errors of the TV and CG images. It is can be seen that the NMSE values of TV images are always lower than the CG images.

Discussion

Conclusion

Acknowledgements

References

1. D. J. Larkman, J. V. Hajnal, A. H. Herlihy,et al. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited.J Magn Reson Imaging. 2001;13(2): 313-317.

2. S. R. Yutzy, N. Seiberlich, J. L. Duerk, et al. Improvements in multislice parallel imaging using radial CAIPIRINHA. Magn Reson Med. 2011;65(4):1630-1637.

3. K. P. Pruessmann, M. Weiger, B. Scheidegger, et al. SENSE: sensitivity encoding for fast MRI. Magn Reson Med.1999;42(2): 952–962.

4. K. T. Block, M. Uecker, J. Frahm. Undersampled radial MRI using multiple coils: iterative image reconstruction using a total variation constraint. Magn Reson Med. 2007;57(6):1086–1098.

5. C. A. McKenzie, E. N. Yeh, Ohliger MA,et al. Self calibrating parallel imaging with automatic coil sensitivity extraction. Magn Reson Med.2002;47(3):529–538.