3841
Improvements in Simultaneous Multislice Imaging Through the Use of SPIRiT and Virtual Conjugate Coils1Biophysics, Medical College of Wisconsin, Milwaukee, WI, United States, 2Radiation Oncology, Biophysics, Radiology, Medical College of Wisconsin, Milwaukee, WI, United States
Synopsis
Simultaneous multislice (SMS) imaging is an attractive solution for accelerating MR acquisition due to its higher inherent SNR. However, further acceleration of SMS images along the phase encoding direction results in increased noise amplification. We demonstrate here the advantages of a combined virtual conjugate coil based phase-constrained SPIRiT reconstruction to minimize the g-factor penalty associated with highly accelerated SMS acquisitions.
Purpose
To improve the quality of multiband MR images by using a phase-constrained SPIRiT reconstruction.Methods
The 2D-SENSE-GRAPPA (2DSG) method1, which solves the through-plane and in-plane unaliasing problem in a single kernel fitting step, has been shown to improve the image quality of highly accelerated SMS acquisitions over typically used slice-GRAPPA2. In 2DSG, the through-plane direction is unaliased by concatenating calibration images along the readout direction, fitting a 2D GRAPPA kernel to the extended FOV calibration k-space, and applying the weights to an aliased k-space.
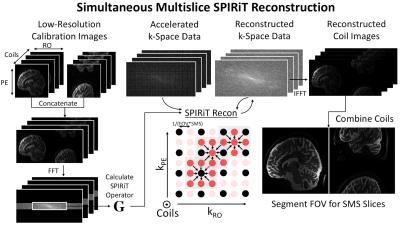
A natural extension of the 2DSG method is to perform a readout extended FOV SPIRiT3 reconstruction. In this manner, the missing data is iteratively computed as a function of neighboring k-space locations regardless of whether they were acquired or synthesized to generate fully sampled k-space data on a coil-by-coil basis (see Figure 1).
Phase-constrained parallel imaging algorithms have been used to improve the SNR of SMS imaging acquisitions4. The virtual conjugate coil (VCC) method provides a way to take advantage of phase differences between slices to provide additional encoding power. VCC data are simply conjugate symmetric copies of actual coil data. The VCC method is commonly used because of its ease of integration with existing parallel imaging algorithms.
We hypothesized that the SNR of in-plane accelerated multiband images would be higher with a SPIRiT reconstruction than with 2DSG or slice-GRAPPA reconstructions since SPIRiT utilizes available data more efficiently. Noisy 16-channel data were simulated for three slices and 100 repetitions with different noise distributions. Interslice shifting of FOV/3 along the phase-encode (PE) direction was performed to simulate CAIPIRINHA acquisition. Low resolution calibration images were generated using the center 24 PE lines and concatenated along the readout direction. The extended FOV images were brought back to k-space and the 2DSG kernels and the GRAPPA operator matrix, G, for the SPIRiT reconstruction were calculated. An in-plane accelerated (R=2) multiband (SMS=3) acquisition was generated by adding the three slices together and discarding every other PE line. The 2DSG, slice-GRAPPA, and SPIRiT reconstructions were performed with and without virtual conjugate coils with kernel sizes of 5x5. The regularized SPIRiT reconstruction was solved via a conjugate gradient algorithm with 40 iterations, and lambda of 1e-03, which were empirically determined to be optimum.
The SNR of each pixel was calculated for all reconstructions as the mean signal intensity divided by the standard deviation from the 100 repetitions. Quantitative g-factor maps were calculated from the SNR maps.
The quality of the SPIRiT reconstructions was also assessed qualitatively in measured simultaneous orthogonal plane imaging5 (SOPI) data acquired on a Siemens Verio 3.0T scanner. This pulse sequence was designed to rapidly acquire images in orthogonal planes for dynamic motion assessment. Sagittal and coronal images were acquired simultaneously with an in-plane reduction factor of R=3. Imaging parameters were: TE1/TE2/TR = 3.17/1.77/5.1 ms, flip angle = 10 degrees, FOV = 340 mm, matrix = 128x128, slice thickness = 5 mm, bandwidth of 100 kHz. Slice-GRAPPA, 2DSG, and SPIRiT reconstructions were performed with and without VCC.
Results
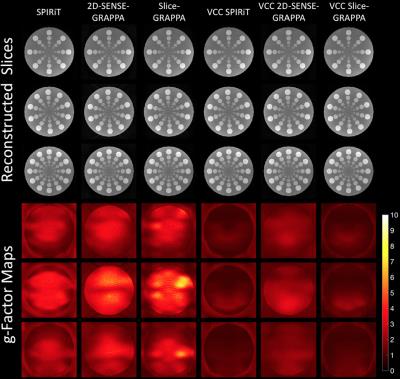
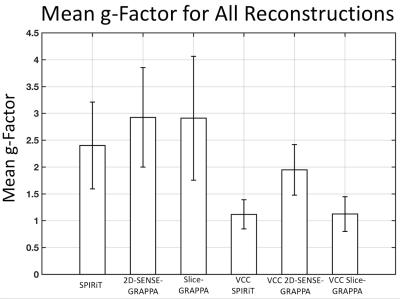
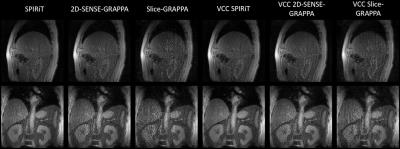
The simulation results are shown in Figure 2. Without VCC phase constraint, the SPIRiT algorithm provided a clear advantage over 2DSG and slice-GRAPPA, evidenced by smaller values in the g-factor maps. With the additional VCC phase constraint, the g-factors for all reconstructions dropped drastically as seen in Figure 3. The SPIRiT + VCC reconstruction yielded the optimum reconstructions. A large improvement in image quality is also seen with a SPIRiT + VCC reconstruction of aliased sagittal and coronal slices acquired with the SOPI pulse sequence (Figure 4).Conclusions
SPIRiT reconstructions with phase constraint provided by virtual conjugate coils improves the image quality simultaneous multislice MR data and should be considered as an alternative method to 2D-SENSE-GRAPPA and slice-GRAPPA reconstructions.Acknowledgements
No acknowledgement found.References
1. Koopmans, P, “Two-dimensional-NCG-SENSE-GRAPPA for fast ghosting-robust reconstruction of in-plane and slice-accelerated blipped-CAIPI Echo Planar Imaging,” Magn. Reson. Med. (In Press, 2016).
2. Setsompop, K, et al, “Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty,” Magn. Reson. Med. 67:1210-1224 (2012).
3. Lustig, M, Pauly, JM, “SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space,” Magn. Reson. Med. 64:457-471 (2010).
4. Blaimer, M, et al, “Multiband phase-constrained parallel MRI,” Mag. Reson. Med. 69:974-980 (2013).
5. Mickevicius, NJ, Paulson, ES, “Simultaneous Orthogonal Plane Imaging,” Mag. Reson. Med. (Accepted, 2016).
Figures