Synopsis

Simultaneous multislice imaging techniques are widely used to accelerate the acquisition process, however, non-ideal coil geometries can introduce noise enhancement. This effect can be reduced by using the virtual-conjugate-coil technique, in which case the g-factors will be dependent of the object background phase. It has been shown that an optimal phasemap exists that minimizes the g-factors. We have used 3D tailored RF pulses to approximate the optimal phase distribution in each simultaneously acquired slice to reduce the noise amplification in phantom and also in vivo. Our results imply that g-factors can be reduced significantly while flip angle homogeneity remains reasonable.

Introduction

In the last few years simultaneous multislice (SMS) techniques have spread rapidly, partly because they avoid the intrinsic loss in SNR corresponding to the square root of the acceleration factor^1,2 of traditional in-plane parallel imaging. However, in both in-plane parallel imaging and SMS, non-ideal coil geometries introduce a spatially dependent noise enhancement usually described by the g-factor.

The recently proposed virtual-conjugate-coil (VCC) phase-constrained imaging³ utilizes symmetry properties of k-space for g-factor reduction. It has been shown that optimizing the object background phase can further improve the g-factor in in-plane acceleration,^4,5 and also that introducing constant phase differences between slices reduces the noise amplification in SMS imaging.⁶

In this work we aim to improve the VCC SMS g-factors even further by optimizing the background phasemap of each simultaneously measured slice using 3D tailored RF pulses.

Methods

Measurements were performed on a clinical 3T scanner (MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany) using prototype sequences. All volunteers gave written informed consent before the study, calculations were performed offline in Matlab (MathWorks, Natick, MA, USA).

First, a prescan was performed with a modified spin-echo EPI sequence, separately measuring 3 axial slices with 3 cm slice distance, using 15° nonselective excitation followed by a slice-selective 180° refocusing pulse. 16 channels of a 20-channel head-neck coil were used for acquisition, with 5 mm slice thickness and 2 mm in-plane resolution. This prescan was repeated using a multiband refocusing pulse to simultaneously measure all slices for later comparison with the optimized measurements.

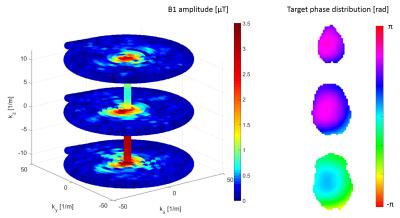
Measurement data were reconstructed offline. Coil combination and coil sensitivity map estimation were performed with ESPIRiT.⁵ Based on the resulting sensitivity maps, the optimized phase distribution was calculated for each slice for a 3-slice SMS measurement, using a derivative-free simplex search algorithm.^3-5 The excitation target phase was taken as the difference of optimized and object phases, followed by an in-plane 8 mm Gaussian smoothing.

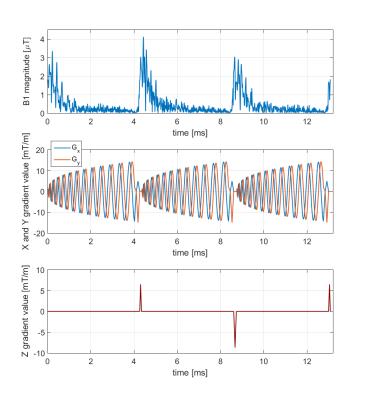
3D excitation RF waveforms were calculated in the small flip angle approximation⁸ using a stack-of-spirals k-space trajectory with 10 mm in-plane excitation resolution and 13 ms pulse length. Exemplary pulse waveform and target phasemap are shown in Figure 1 and Figure 2. Tailored RF pulses were subsequently applied in separate measurements using the same protocol as the prescans, first measuring all slices separately, then using a multiband refocusing pulse to simultaneously acquire all slices.

Reconstruction was performed offline using a SENSE-GRAPPA hybrid⁹ for both conventional and tailored excitation, with and without using the VCC method. Furthermore, VCC reconstruction was performed on a simulated dataset as well, created by retrospectively adding a synthetic slice-specific phaseshift of $$$\frac{\pi}{2} \times sliceindex$$$ for each slice of the conventional scan, as it can be benefical for the VCC reconstruction.⁶ GRAPPA kernels were trained on the datasets of separately measured slices and applied to the SMS acquisitions. G-factor maps were computed from the GRAPPA kernels.¹⁰

Standard deviation of the voxel-wise difference between conventional and optimized scans was calculated as a measure of flip angle inhomogeneity.

Results

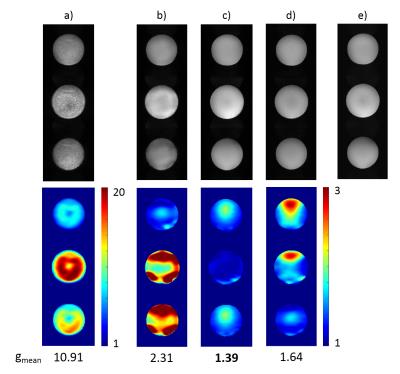
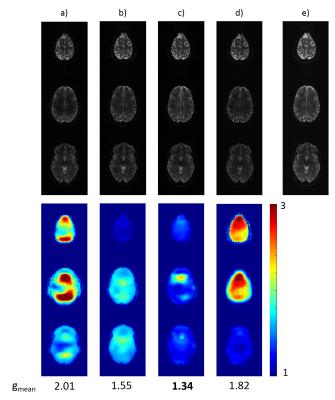
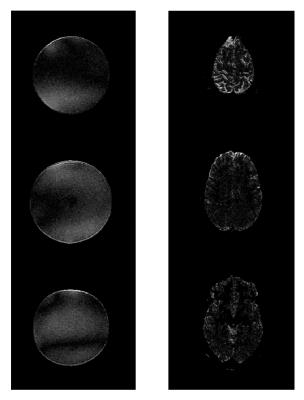
Reconstructed sum-of-squares images as well as the calculated g-factor maps for conventional and optimized excitation, with and without including the VCC signals, are shown in Figure 3 and Figure 4 for phantom and human measurements, respectively. Although the reconstruction quality is already improved by solely including the VCC signal, it can be clearly seen that g-factors can be further decreased significantly by optimizing the object phase with the tailored pulses, as this setup outperforms all the others in mean g-factors.

Besides introducing the optimal phase distributions, the tailored pulses also produce reasonably homogeneous flip angle distributions. Magnitude differences between conventional and optimized scans are shown in Figure 5 with 10x amplification and same windowing as the reconstructed images. Standard deviation of the magnitude difference is 8% and 18% of the mean intensity in phantom and in vivo, respectively.

Discussion

We have shown that using VCC reconstruction and 3D tailored RF pulses designed to optimize the background phase for each slice, g-factors in simultaneous multislice imaging can be decreased significantly while spatial flip angle homogeneity remains reasonable. Although RF pulse length increases with the number of slices, it could be reduced using parallel transmission, making higher slice accelerations feasible.

Using advanced pulse design algorithms could allow to incorporate slice selection into the excitation, thus enabling the application of non-spin-echo-based sequences, where the benefit of phase optimization is expected to be even higher.

As a next step the concept of optimizing the background phase is being extended for CAIPIRINHA methods.^2,11

Acknowledgements

Á. K. and V. Z. were supported by a grant from the Hungarian Brain Research Program (KTIA_13_NAP-AI/18).

The authors thank James G. Pipe for spiral gradient waveform calculation code, and Michael Lustig for ESPIRiT code.

References

1. Barth M, Breuer F, Koopmans PJ, Norris DG, Poser BA. Simultaneous multislice (SMS) imaging techniques. Magn. Reson. Med. 2016;75(1):63-81.

2. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-Controlled Aliasing in Parallel Imaging (blipped-CAIPI) for simultaneous multi-slice EPI with reduced g-factor penalty. Magn. Reson. Med. 2012;67(5):1210-1224.

3. Blaimer M, Gutberlet M, Kellman P, Breuer FA, Köstler H, Griswold MA. Virtual coil concept for improved parallel MRI employing conjugate symmetric signals. Magn. Reson. Med. 2009;61(1):93-102.

4. Schneider JT, Blaimer M, Ullmann P. (2012). Tailoring the image background phase by spatially selective excitation for improved parallel imaging reconstruction performance. Proceedings of the 20th Annual Meeting of ISMRM, Melbourne, Australia; 2012.

5. Kettinger A, Kannengiesser SAR, Breuer FA, Vidnyanszky Z, Blaimer M. Tailored RF pulses for optimized phase-constrained parallel imaging: initial experience on a clinical system. Proceedings of the 33rd Annual Scientific Meeting of the ESMRMB, Vienna, Austria; 2016.

6. Blaimer M, Choli M, Jakob PM, Griswold MA, Breuer FA. Multiband phase-constrained parallel MRI. Magn. Reson. Med. 2013;69:974–980.

7. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Lustig M, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn. Reson. Med. 2014;71(3):990-1001.

8. Yip CY, Fessler JA, Noll DC. Iterative RF pulse design for multidimensional, small-tip-angle selective excitation. Magn. Reson. Med. 2005;54(4):908-917.

9. Blaimer M, Breuer FA, Seiberlich N, Mueller MF, Heidemann RM, Jellus V, Jakob PM, et al. Accelerated volumetric MRI with a SENSE/GRAPPA combination. J. Magn. Reson. Imaging, 2006;24(2):444-450.

10. Breuer FA, Kannengiesser SAR, Blaimer M, Seiberlich N, Jakob PM, Griswold MA. General formulation for quantitative G-factor calculation in GRAPPA reconstructions. Magn. Reson. Med. 2009;62(3):739-746.

11. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn. Reson. Med. 2005;53(3):684-691.